人教版七年级数学上册第三章《一元一次方程》期末培优训练题 (1)(含答案)
文档属性
| 名称 | 人教版七年级数学上册第三章《一元一次方程》期末培优训练题 (1)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 41.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 00:00:00 | ||
图片预览




文档简介
第三章《一元一次方程》期末培优训练题
一、选择题
1.下列选项中,是一元一次方程的为( )
A. B. C.3+7=10 D.x +2x+1=0
2. 运用等式性质进行的变形,正确的是( )
A.如果,那么a=b B.如果a=b,那么
C.如果a=b,那么a+c=b﹣c D.如果a2=3a,那么a=3
3.根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是,若输入x的值是,则输出y的值是( )
A.5 B.19 C.0 D.21
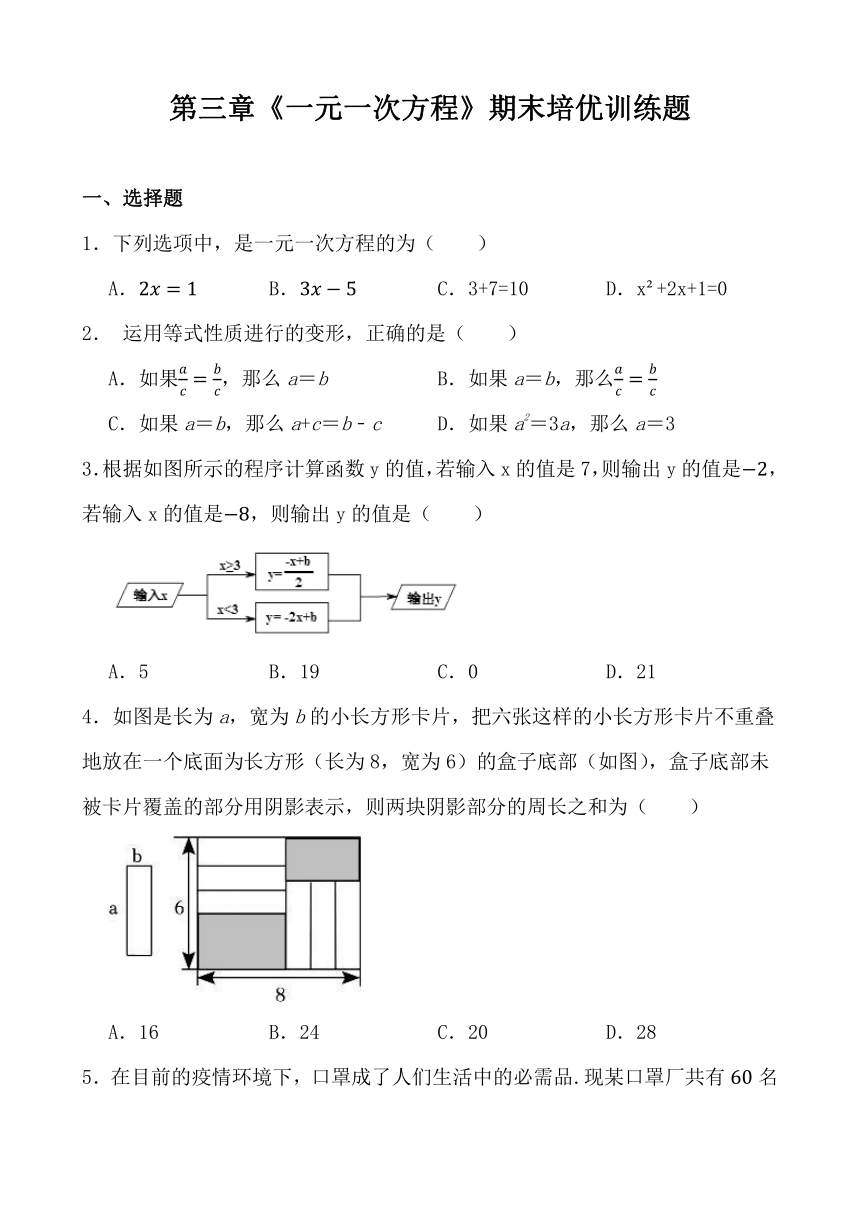
4.如图是长为a,宽为b的小长方形卡片,把六张这样的小长方形卡片不重叠地放在一个底面为长方形(长为8,宽为6)的盒子底部(如图),盒子底部未被卡片覆盖的部分用阴影表示,则两块阴影部分的周长之和为( )
A.16 B.24 C.20 D.28
5.在目前的疫情环境下,口罩成了人们生活中的必需品.现某口罩厂共有名工人,每名工人每天可以生产个罩面或个耳绳.已知一个罩面需要配两个耳绳,为使每天生产的罩面和耳绳刚好配套,设安排名员工生产罩面,则下列方程正确的是( )
A. B.
C. D.
二、填空题
6.若是一元一次方程,则 .
7.已知是关于的方程的解,则的值是 .
8.已知a,b为定值,且无论k为何值,关于x的方程的解总是,则 = .
9.当x= 时,1-x与的值相等.
10.把方程2x+y=1改写成用含x的式子表示y的形式,则y= .
11.商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的利润率为30%,每个大书包的利润率为20%,如果该商店某日出售大书包5个,小书包10 个,则这一天该商店出售书包的利润额是 元.
12.某村组织村委领导共同种一批树苗,如果每人种12棵,则剩下5棵树苗;如果每人种14棵,则缺7棵树苗,则这批树苗有 棵.
13.小云的爸爸现在的年龄比小云大25岁,5年后小云爸爸的年龄是小云的2倍少10岁,小云现在岁 .
14.解诗谜:悟空顺风探妖踪,千里只用四分钟;归时四分行六百,试问风速是多少?题目的意思是:孙悟空追寻妖精的行踪,去时顺风,1000里只用了4分钟;回来时逆风,4分钟只走了600里,试求风的速度为 .
三、解答题
15.解方程:
(1);
(2).
16.当为何值时,代数式比大1.
17.已知 与 互为相反数,求a的值.
18.如图,AB=30cm,点P从点A出发,沿AB以3cm/s的速度匀速向终点B运动;同时点Q从点B出发,沿BA以5cm/s的速度匀速向终点A运动.设运动时间为t.
(1)填空:PA= cm: BQ= cm (用含t的代数式表示).
(2)当P、Q两点相遇时,求t的值.
(3)直接写出P、Q两点相距6cm时,t的值为
19.某校班级篮球联赛中,每场比赛都要分胜负,每队胜1场得3分,负1场得1分,如果某班在第一轮的28场比赛中得48分,那么这个班胜了多少场?
20.某市收取水费规定如下:每月每户用水若不超过20立方米,则每立方米水价为2.5元;若超过20立方米,则超过部分每立方米按4.0元收费.某户居民在某月所交水费的平均水价为每立方米3.0元,那么这户居民这个月共用了多少立方米的水?
21.某学校计划今年国庆期间组织部分教师到外地进行学习,预订宾馆住宿时,有住宿条件完全一样的甲、乙两家宾馆可供选择,其收费标准均为每人每天120元,并且各自推出不同的优惠方案.
【问题信息】外出学习教师不超过100人.甲宾馆是35人以内(含35人)按标准收费,超过35人的,超出部分按九折收费;乙宾馆是45人以内(含45人)的按标准收费,超过45人的,超出部分按八折收费.
【问题设计】如果你是这个学校负责人,你会怎样选择宾馆?请你给出你的设计方案和理由.
答案解析部分
1.A
2.A
3.B
4.B
5.D
6.
7.1
8.
9.2
10.
11.90
12.77
13.30
14.50里/分钟
15.(1)解:去括号,得:,移项、合并同类项,得:,
系数化为1,得:
(2)解:去分母,得:,
去括号,得:,移项、合并同类项,得:,系数化为1,得:.
16.解:根据题意得,解得,满足条件的的值为.
17.解:由题意,得 ,
去分母得:
合并同类项得:
解得a=5.
18.(1)3t;5t
(2)解:由题意得:3t+5t=30,
解得t=
答: 当P、Q两点相遇时,求t的值为
(3)t=3或t=4.5
19.解:设这个班胜了x场,则负(28﹣x)场,根据题意得:3x+(28﹣x)=48,解得:x=10.答:这个班胜了10场
20.解:设这户居民这个月共用水x立方米,则20×2.5+(x-20)×4=3x,解得x=30.
21.解:解:设共有x(x≤100)名教师到外地进行学习.
当x≤35时,选择甲宾馆所需费用为120x元,选择乙宾馆所需费用为120x元,
∵120x=120x,
∴此时选择两宾馆所需费用相同,即可以任意选择甲、乙两家宾馆;
当35<x≤45时,选择甲宾馆所需费用为120×35+120×0.9(x-35)=(108x+420)元,选择乙宾馆所需费用为120x元,
∵108x+420<120x,
∴此时选择甲宾馆所需费用较少;
当45<x≤100时,选择甲宾馆所需费用为120×35+120×0.9(x-35)=(108x+420)元,选择乙宾馆所需费用为120×45+120×0.8(x-45)=(96x+1080)元,
若108x+420<96x+1080,则x<55,此时选择甲宾馆所需费用较少;
若108x+420=96x+1080,则x=55,此时选择两宾馆所需费用相同;
若108x+420>96x+1080,则x>55,此时选择乙宾馆所需费用较少.
综上所述,方案设计为:当x≤35或x=55时,选择两宾馆所需费用相同;当35<x<55时,选择甲宾馆更实惠;当55<x≤100时,选择乙宾馆更实惠.
一、选择题
1.下列选项中,是一元一次方程的为( )
A. B. C.3+7=10 D.x +2x+1=0
2. 运用等式性质进行的变形,正确的是( )
A.如果,那么a=b B.如果a=b,那么
C.如果a=b,那么a+c=b﹣c D.如果a2=3a,那么a=3
3.根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是,若输入x的值是,则输出y的值是( )
A.5 B.19 C.0 D.21
4.如图是长为a,宽为b的小长方形卡片,把六张这样的小长方形卡片不重叠地放在一个底面为长方形(长为8,宽为6)的盒子底部(如图),盒子底部未被卡片覆盖的部分用阴影表示,则两块阴影部分的周长之和为( )
A.16 B.24 C.20 D.28
5.在目前的疫情环境下,口罩成了人们生活中的必需品.现某口罩厂共有名工人,每名工人每天可以生产个罩面或个耳绳.已知一个罩面需要配两个耳绳,为使每天生产的罩面和耳绳刚好配套,设安排名员工生产罩面,则下列方程正确的是( )
A. B.
C. D.
二、填空题
6.若是一元一次方程,则 .
7.已知是关于的方程的解,则的值是 .
8.已知a,b为定值,且无论k为何值,关于x的方程的解总是,则 = .
9.当x= 时,1-x与的值相等.
10.把方程2x+y=1改写成用含x的式子表示y的形式,则y= .
11.商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的利润率为30%,每个大书包的利润率为20%,如果该商店某日出售大书包5个,小书包10 个,则这一天该商店出售书包的利润额是 元.
12.某村组织村委领导共同种一批树苗,如果每人种12棵,则剩下5棵树苗;如果每人种14棵,则缺7棵树苗,则这批树苗有 棵.
13.小云的爸爸现在的年龄比小云大25岁,5年后小云爸爸的年龄是小云的2倍少10岁,小云现在岁 .
14.解诗谜:悟空顺风探妖踪,千里只用四分钟;归时四分行六百,试问风速是多少?题目的意思是:孙悟空追寻妖精的行踪,去时顺风,1000里只用了4分钟;回来时逆风,4分钟只走了600里,试求风的速度为 .
三、解答题
15.解方程:
(1);
(2).
16.当为何值时,代数式比大1.
17.已知 与 互为相反数,求a的值.
18.如图,AB=30cm,点P从点A出发,沿AB以3cm/s的速度匀速向终点B运动;同时点Q从点B出发,沿BA以5cm/s的速度匀速向终点A运动.设运动时间为t.
(1)填空:PA= cm: BQ= cm (用含t的代数式表示).
(2)当P、Q两点相遇时,求t的值.
(3)直接写出P、Q两点相距6cm时,t的值为
19.某校班级篮球联赛中,每场比赛都要分胜负,每队胜1场得3分,负1场得1分,如果某班在第一轮的28场比赛中得48分,那么这个班胜了多少场?
20.某市收取水费规定如下:每月每户用水若不超过20立方米,则每立方米水价为2.5元;若超过20立方米,则超过部分每立方米按4.0元收费.某户居民在某月所交水费的平均水价为每立方米3.0元,那么这户居民这个月共用了多少立方米的水?
21.某学校计划今年国庆期间组织部分教师到外地进行学习,预订宾馆住宿时,有住宿条件完全一样的甲、乙两家宾馆可供选择,其收费标准均为每人每天120元,并且各自推出不同的优惠方案.
【问题信息】外出学习教师不超过100人.甲宾馆是35人以内(含35人)按标准收费,超过35人的,超出部分按九折收费;乙宾馆是45人以内(含45人)的按标准收费,超过45人的,超出部分按八折收费.
【问题设计】如果你是这个学校负责人,你会怎样选择宾馆?请你给出你的设计方案和理由.
答案解析部分
1.A
2.A
3.B
4.B
5.D
6.
7.1
8.
9.2
10.
11.90
12.77
13.30
14.50里/分钟
15.(1)解:去括号,得:,移项、合并同类项,得:,
系数化为1,得:
(2)解:去分母,得:,
去括号,得:,移项、合并同类项,得:,系数化为1,得:.
16.解:根据题意得,解得,满足条件的的值为.
17.解:由题意,得 ,
去分母得:
合并同类项得:
解得a=5.
18.(1)3t;5t
(2)解:由题意得:3t+5t=30,
解得t=
答: 当P、Q两点相遇时,求t的值为
(3)t=3或t=4.5
19.解:设这个班胜了x场,则负(28﹣x)场,根据题意得:3x+(28﹣x)=48,解得:x=10.答:这个班胜了10场
20.解:设这户居民这个月共用水x立方米,则20×2.5+(x-20)×4=3x,解得x=30.
21.解:解:设共有x(x≤100)名教师到外地进行学习.
当x≤35时,选择甲宾馆所需费用为120x元,选择乙宾馆所需费用为120x元,
∵120x=120x,
∴此时选择两宾馆所需费用相同,即可以任意选择甲、乙两家宾馆;
当35<x≤45时,选择甲宾馆所需费用为120×35+120×0.9(x-35)=(108x+420)元,选择乙宾馆所需费用为120x元,
∵108x+420<120x,
∴此时选择甲宾馆所需费用较少;
当45<x≤100时,选择甲宾馆所需费用为120×35+120×0.9(x-35)=(108x+420)元,选择乙宾馆所需费用为120×45+120×0.8(x-45)=(96x+1080)元,
若108x+420<96x+1080,则x<55,此时选择甲宾馆所需费用较少;
若108x+420=96x+1080,则x=55,此时选择两宾馆所需费用相同;
若108x+420>96x+1080,则x>55,此时选择乙宾馆所需费用较少.
综上所述,方案设计为:当x≤35或x=55时,选择两宾馆所需费用相同;当35<x<55时,选择甲宾馆更实惠;当55<x≤100时,选择乙宾馆更实惠.
