北师大版数学二上 有多少点子 教学设计
文档属性
| 名称 | 北师大版数学二上 有多少点子 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 582.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览




文档简介
《有多少点子》教学设计
教材分析
《有多少点子》是北师大版小学数学三册第三单元,数一数与乘法中第三课时的内容。乘法意义的学习是学生学习乘法的开始,是学习乘法口诀的直接基础,也是进一步学习较复杂的乘法计算及其应用的重要基础。为了让学生更好地掌握这一重要知识,新教材增加了《有多少点子》这一内容。在学习本课之前,学生已经明白了学习乘法的必要性;初步认识了乘法的意义;知道了乘法各部分的名称。本课的学习旨在:通过点子图这一直观模型加强学生对乘法意义进一步的理解,帮助学生在头脑中建立乘法的模型。
教学目标
1、理解一个加法算式能写出两个乘法算式,一个乘法算式对应两个不同的加法算式和两个不同的意义。
2、用两种不同的方法(横着数或竖着数)数排列整齐的点子的个数,并列出乘法算式。
3、通过计算点子的数量,进一步体会加法和乘法之间的联系,初步学习用乘法解决问题。
教学重难点
重点
理解图示、算式及算式所对应的意义三者之间的关系。
难点
理解一个加法算式能写出两个乘法算式,一个乘法算式对应两个不同的加法算式和两个不同的意义。
教学过程
【回顾旧知,深化理解】
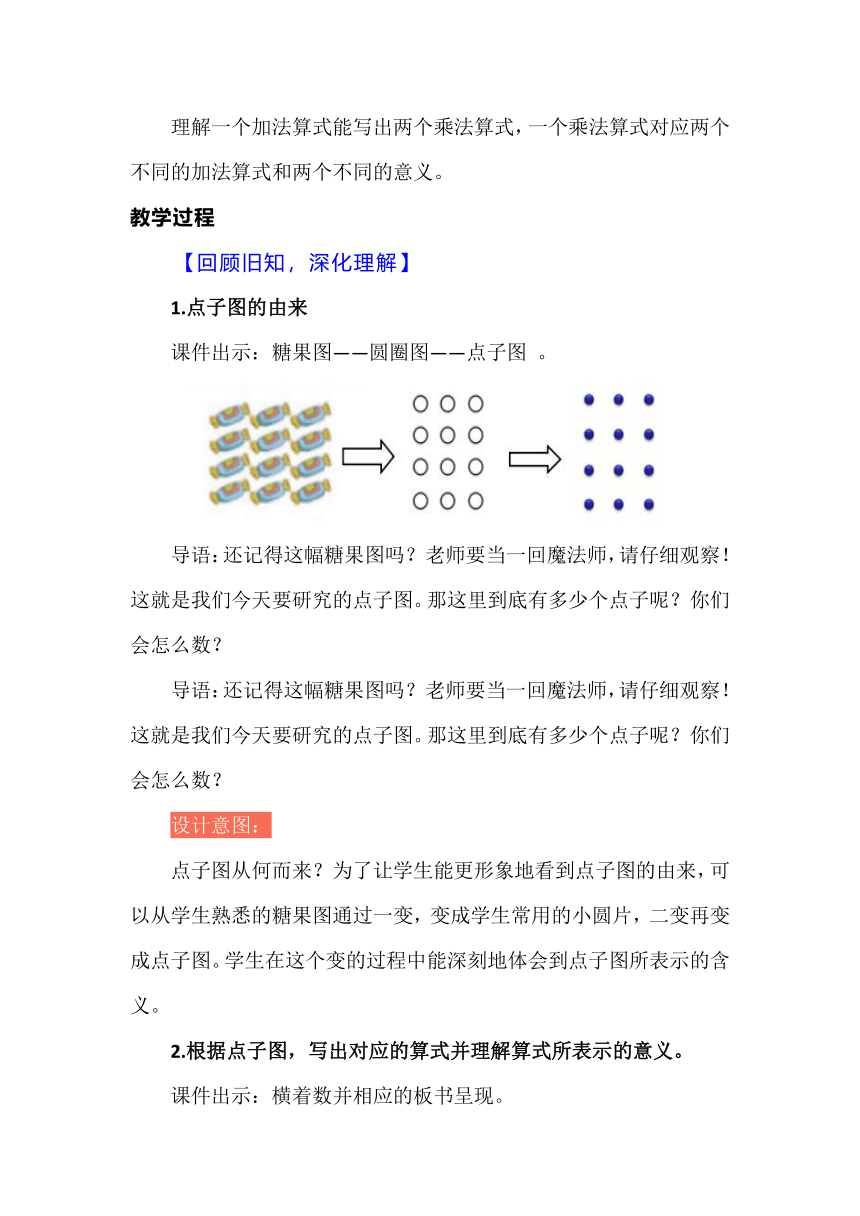
1.点子图的由来
课件出示:糖果图——圆圈图——点子图 。
导语:还记得这幅糖果图吗?老师要当一回魔法师,请仔细观察!这就是我们今天要研究的点子图。那这里到底有多少个点子呢?你们会怎么数?
导语:还记得这幅糖果图吗?老师要当一回魔法师,请仔细观察!这就是我们今天要研究的点子图。那这里到底有多少个点子呢?你们会怎么数?
设计意图:
点子图从何而来?为了让学生能更形象地看到点子图的由来,可以从学生熟悉的糖果图通过一变,变成学生常用的小圆片,二变再变成点子图。学生在这个变的过程中能深刻地体会到点子图所表示的含义。
2.根据点子图,写出对应的算式并理解算式所表示的意义。
课件出示:横着数并相应的板书呈现。
(横着数:引导学生一边数,一边做动作:唰一行,1个3;唰两行,2个3;唰三行,3个3,唰四行,4个3)
提问:我们来看看横着数,我们数出了4行(电脑出示:4行)你能列出哪些算式呢?
(根据学生的回答相机板书。)
3+3+3+3=12, 3×4=12, 4×3=12
追问1:这个加法算式表示什么意思?
表示4个3相加的和是多少?
追问2:4×3=12表示什么?3×4=12呢?
4×3=12表示4个3相加的和是多少?3×4=12也表示4个3相加的和是多少?
追问2:仔细观察,你发现了什么?
(三个算式都表示4个3相加的和是多少?)
课件出示:
(竖着数:引导学生一边数,一边做动作:唰一列,1个4;唰两列,2个4;唰三列,3个4)
提问:仔细观察,竖着数我们数出了3列,可以列出几个算式?分别是哪几个?
4+4+4=12, 3×4=12, 4×3=12
追问:这几个算式都表示什么意思?
(三个算式都表示3个4相加的和是多少?)
设计意图:
从不同的角度数点子,发现横着数可以得到一个加法算式,两个乘法算式以及三个算式对应同一个意义;竖着数同样可以得到相同的结果。这既是对旧知的回顾,又是一次提升式的小结。
3.观察、比较、类推、迁移
过渡:刚刚我们通过两种角度观察同一幅图:横着圈数出4行;竖着圈数出3列,那我们就把这样的点子图叫做4行3列的点子图。
提问:那像这样4行3列的点子图,你们一共可以列出几个算式呢?(6个)
追问:仔细观察(或手势辅助)你有什么发现?
①学生发现重复算式。
②一个乘法可以对应两个加法算式,两个意义。一个加法只能对应一个意义。
提问:4×3为什么可以表示两个加法算式,加法算式不一样,又说明了什么?
(4×3表示4个3相加的和是多少,又表示3个4相加的和是多少;不同的加法算式意义也不同。)
③两个不同的加法算式可以用同一个乘法算式来表示。
课件变颜色,提问:既然这两个算式相同,那能重叠吗?
开放式追问:这样一重叠,刚才我们发现的秘密是不是更加清楚了呢,你们能再说一说自己的发现吗?
(观察的角度不同,列出的加法算式也是不同的,一个加法算式只能表示一个意义。所以一个乘法表示出的两个加法算式就有两种不同的意义。但计算结果都相同。)
过渡:这样一个4行3列的点子图,通过横看和竖看发现一共可以列出6个算式,其中两个乘法算式是相同的。那老师变个魔术,看看你们又有什么新发现?
提问:这个点子图现在变成了几行几列了呢?你能像刚刚我们研究4行3列的点子图一样来说一说这幅图身上藏着的知识吗?(学生说,教师板书)
结论:一般情况下,同一幅点子图,观察角度不同,表示的意义就不同,列出的加法算式就不同(相同加数不同,相同加数的个数也不同),但却可以用同一个乘法算式来表示。
设计意图:
通过计算点子的数量,进一步体会加法和乘法之间的联系 。同时引导学生感悟知识的内在联系,通过观察,比较,类推和迁移进一步理解乘法的含义。
02活动一:
根据点子图写算式,说意义
1.说一说,摆一摆
过渡:小朋友们真是会思考,研究出了这么多知识,让我们看看课件老师是不是也是这么研究的。(播放课件)看来到最后同一幅点子图可以有两种观察角度,列出4个算式。同一个乘法算式又可以有两种点子图的摆法,研究来研究去原来我们就是在研究有多少个点子。(揭题板书:有多少点子)其实淘气和笑笑也和你们一样在研究点子图,请看书上第20页的绿点一。
提问:淘气和笑笑在研究怎样的点子图?你看懂了什么 (请大家在自己准备的点子图上也学着摆一摆,然后说一说你的发现。)
预设:这是一个3行2列的点子图
预设2:根据这幅点子图,淘气和笑笑列出了一个加法算式,两个乘法算式。
追问:你们觉得淘气和笑笑是从哪个角度来怎么研究的?(横着数)。
追问2:老师猜你们还知道这三个算式的意义。(三个算式都表示3个2相加的和是多少?)
2.设疑补充
过渡:笑笑和淘气只研究了一种角度,知道的还没有你们的多,你们能把他们没有研究出来的补充一下吗?
课件出示,合并两个乘法算式。
提问:你们补的和电脑老师一样吗?旋转以后的点子图是不是也一样呢?(如下图所示)
3.独自补充图2的相关知识
提问:像刚才这样补,这样看,你们会补了吗?请同学们自己将图2进行补充。
设计意图:
在此活动中引导学生做一做,说一说,不仅使学生在自己的操作过程中体验说的道理,领悟乘法的意义,由能使学生感受到,由于观察的角度不同,看成的相同加数以及相同加数的个数也不同,但所列的乘法算式计算结果相同。在后面出示 5×5 的点子时,学生能很自然的得出自己的发现。
03活动二:
根据乘法算式摆点子图
提问:刚刚两种不同的摆法都可以表示同一个乘法算式,那么如果给你一个乘法算式4×7,你会想到怎样的点子图呢?看看绿点2,淘气和笑笑摆出了怎样的两幅点子图?和你摆的一样吗?
追问:4×7在图1中可以表示几个意义?图2呢?
结论:一个乘法算式可以摆出两幅点子图,表示两种意义。
追问3:绿点2告诉我们一个乘法可以有两种摆法,板书中也发现一个乘法有两种摆法,那现在没有了遮挡板,读绿点三,你能用在下面这么多的点子里面用一个大圈圈出3×8吗?让我们动手试一试吧。
设计意图:
学生经过“活动一”理解了乘法的意义,这在“活动二”中带来的直接效果就是,学生能自己进行摸索着看乘法算式摆点子图,也就是能通过反向思维,进一步理解乘法的意义。在总结时,不少学生能根据自己的活动经验,将操作方法表达出来。而且学生还能发现,虽然摆的方法不一样,数的方法也不一样,但是都可以用两个乘法算式来表示,而且点子数都相同。
04【总结与拓展】
总结:学完本节课,你有什么收获呢?
拓展:那是不是所有的点子图都能表示出4个算式呢?请小朋友想一想。
结论:当加数和加数个数相同的况下,一个乘法只对应一个点子图和一个意义。比如5×5=25,只能摆出5行5列的点子图,也只能表示5个5。
05板书设计:
教材分析
《有多少点子》是北师大版小学数学三册第三单元,数一数与乘法中第三课时的内容。乘法意义的学习是学生学习乘法的开始,是学习乘法口诀的直接基础,也是进一步学习较复杂的乘法计算及其应用的重要基础。为了让学生更好地掌握这一重要知识,新教材增加了《有多少点子》这一内容。在学习本课之前,学生已经明白了学习乘法的必要性;初步认识了乘法的意义;知道了乘法各部分的名称。本课的学习旨在:通过点子图这一直观模型加强学生对乘法意义进一步的理解,帮助学生在头脑中建立乘法的模型。
教学目标
1、理解一个加法算式能写出两个乘法算式,一个乘法算式对应两个不同的加法算式和两个不同的意义。
2、用两种不同的方法(横着数或竖着数)数排列整齐的点子的个数,并列出乘法算式。
3、通过计算点子的数量,进一步体会加法和乘法之间的联系,初步学习用乘法解决问题。
教学重难点
重点
理解图示、算式及算式所对应的意义三者之间的关系。
难点
理解一个加法算式能写出两个乘法算式,一个乘法算式对应两个不同的加法算式和两个不同的意义。
教学过程
【回顾旧知,深化理解】
1.点子图的由来
课件出示:糖果图——圆圈图——点子图 。
导语:还记得这幅糖果图吗?老师要当一回魔法师,请仔细观察!这就是我们今天要研究的点子图。那这里到底有多少个点子呢?你们会怎么数?
导语:还记得这幅糖果图吗?老师要当一回魔法师,请仔细观察!这就是我们今天要研究的点子图。那这里到底有多少个点子呢?你们会怎么数?
设计意图:
点子图从何而来?为了让学生能更形象地看到点子图的由来,可以从学生熟悉的糖果图通过一变,变成学生常用的小圆片,二变再变成点子图。学生在这个变的过程中能深刻地体会到点子图所表示的含义。
2.根据点子图,写出对应的算式并理解算式所表示的意义。
课件出示:横着数并相应的板书呈现。
(横着数:引导学生一边数,一边做动作:唰一行,1个3;唰两行,2个3;唰三行,3个3,唰四行,4个3)
提问:我们来看看横着数,我们数出了4行(电脑出示:4行)你能列出哪些算式呢?
(根据学生的回答相机板书。)
3+3+3+3=12, 3×4=12, 4×3=12
追问1:这个加法算式表示什么意思?
表示4个3相加的和是多少?
追问2:4×3=12表示什么?3×4=12呢?
4×3=12表示4个3相加的和是多少?3×4=12也表示4个3相加的和是多少?
追问2:仔细观察,你发现了什么?
(三个算式都表示4个3相加的和是多少?)
课件出示:
(竖着数:引导学生一边数,一边做动作:唰一列,1个4;唰两列,2个4;唰三列,3个4)
提问:仔细观察,竖着数我们数出了3列,可以列出几个算式?分别是哪几个?
4+4+4=12, 3×4=12, 4×3=12
追问:这几个算式都表示什么意思?
(三个算式都表示3个4相加的和是多少?)
设计意图:
从不同的角度数点子,发现横着数可以得到一个加法算式,两个乘法算式以及三个算式对应同一个意义;竖着数同样可以得到相同的结果。这既是对旧知的回顾,又是一次提升式的小结。
3.观察、比较、类推、迁移
过渡:刚刚我们通过两种角度观察同一幅图:横着圈数出4行;竖着圈数出3列,那我们就把这样的点子图叫做4行3列的点子图。
提问:那像这样4行3列的点子图,你们一共可以列出几个算式呢?(6个)
追问:仔细观察(或手势辅助)你有什么发现?
①学生发现重复算式。
②一个乘法可以对应两个加法算式,两个意义。一个加法只能对应一个意义。
提问:4×3为什么可以表示两个加法算式,加法算式不一样,又说明了什么?
(4×3表示4个3相加的和是多少,又表示3个4相加的和是多少;不同的加法算式意义也不同。)
③两个不同的加法算式可以用同一个乘法算式来表示。
课件变颜色,提问:既然这两个算式相同,那能重叠吗?
开放式追问:这样一重叠,刚才我们发现的秘密是不是更加清楚了呢,你们能再说一说自己的发现吗?
(观察的角度不同,列出的加法算式也是不同的,一个加法算式只能表示一个意义。所以一个乘法表示出的两个加法算式就有两种不同的意义。但计算结果都相同。)
过渡:这样一个4行3列的点子图,通过横看和竖看发现一共可以列出6个算式,其中两个乘法算式是相同的。那老师变个魔术,看看你们又有什么新发现?
提问:这个点子图现在变成了几行几列了呢?你能像刚刚我们研究4行3列的点子图一样来说一说这幅图身上藏着的知识吗?(学生说,教师板书)
结论:一般情况下,同一幅点子图,观察角度不同,表示的意义就不同,列出的加法算式就不同(相同加数不同,相同加数的个数也不同),但却可以用同一个乘法算式来表示。
设计意图:
通过计算点子的数量,进一步体会加法和乘法之间的联系 。同时引导学生感悟知识的内在联系,通过观察,比较,类推和迁移进一步理解乘法的含义。
02活动一:
根据点子图写算式,说意义
1.说一说,摆一摆
过渡:小朋友们真是会思考,研究出了这么多知识,让我们看看课件老师是不是也是这么研究的。(播放课件)看来到最后同一幅点子图可以有两种观察角度,列出4个算式。同一个乘法算式又可以有两种点子图的摆法,研究来研究去原来我们就是在研究有多少个点子。(揭题板书:有多少点子)其实淘气和笑笑也和你们一样在研究点子图,请看书上第20页的绿点一。
提问:淘气和笑笑在研究怎样的点子图?你看懂了什么 (请大家在自己准备的点子图上也学着摆一摆,然后说一说你的发现。)
预设:这是一个3行2列的点子图
预设2:根据这幅点子图,淘气和笑笑列出了一个加法算式,两个乘法算式。
追问:你们觉得淘气和笑笑是从哪个角度来怎么研究的?(横着数)。
追问2:老师猜你们还知道这三个算式的意义。(三个算式都表示3个2相加的和是多少?)
2.设疑补充
过渡:笑笑和淘气只研究了一种角度,知道的还没有你们的多,你们能把他们没有研究出来的补充一下吗?
课件出示,合并两个乘法算式。
提问:你们补的和电脑老师一样吗?旋转以后的点子图是不是也一样呢?(如下图所示)
3.独自补充图2的相关知识
提问:像刚才这样补,这样看,你们会补了吗?请同学们自己将图2进行补充。
设计意图:
在此活动中引导学生做一做,说一说,不仅使学生在自己的操作过程中体验说的道理,领悟乘法的意义,由能使学生感受到,由于观察的角度不同,看成的相同加数以及相同加数的个数也不同,但所列的乘法算式计算结果相同。在后面出示 5×5 的点子时,学生能很自然的得出自己的发现。
03活动二:
根据乘法算式摆点子图
提问:刚刚两种不同的摆法都可以表示同一个乘法算式,那么如果给你一个乘法算式4×7,你会想到怎样的点子图呢?看看绿点2,淘气和笑笑摆出了怎样的两幅点子图?和你摆的一样吗?
追问:4×7在图1中可以表示几个意义?图2呢?
结论:一个乘法算式可以摆出两幅点子图,表示两种意义。
追问3:绿点2告诉我们一个乘法可以有两种摆法,板书中也发现一个乘法有两种摆法,那现在没有了遮挡板,读绿点三,你能用在下面这么多的点子里面用一个大圈圈出3×8吗?让我们动手试一试吧。
设计意图:
学生经过“活动一”理解了乘法的意义,这在“活动二”中带来的直接效果就是,学生能自己进行摸索着看乘法算式摆点子图,也就是能通过反向思维,进一步理解乘法的意义。在总结时,不少学生能根据自己的活动经验,将操作方法表达出来。而且学生还能发现,虽然摆的方法不一样,数的方法也不一样,但是都可以用两个乘法算式来表示,而且点子数都相同。
04【总结与拓展】
总结:学完本节课,你有什么收获呢?
拓展:那是不是所有的点子图都能表示出4个算式呢?请小朋友想一想。
结论:当加数和加数个数相同的况下,一个乘法只对应一个点子图和一个意义。比如5×5=25,只能摆出5行5列的点子图,也只能表示5个5。
05板书设计:
