第六章 图形的相似 复习课件(共36张PPT)
文档属性
| 名称 | 第六章 图形的相似 复习课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 05:27:20 | ||
图片预览








文档简介
(共36张PPT)
图形的相似
苏教版九年级下册
图形的相似
制作:没烦恼
6.6 图形的位似
6.7 用相似三角形解决问题
6.1 图上距离与实际距离
6.2 黄金分割
6.3 相似图形
6.4 探索三角形相似的条件
6.5 相似三角形的性质
CONTENTS
目录
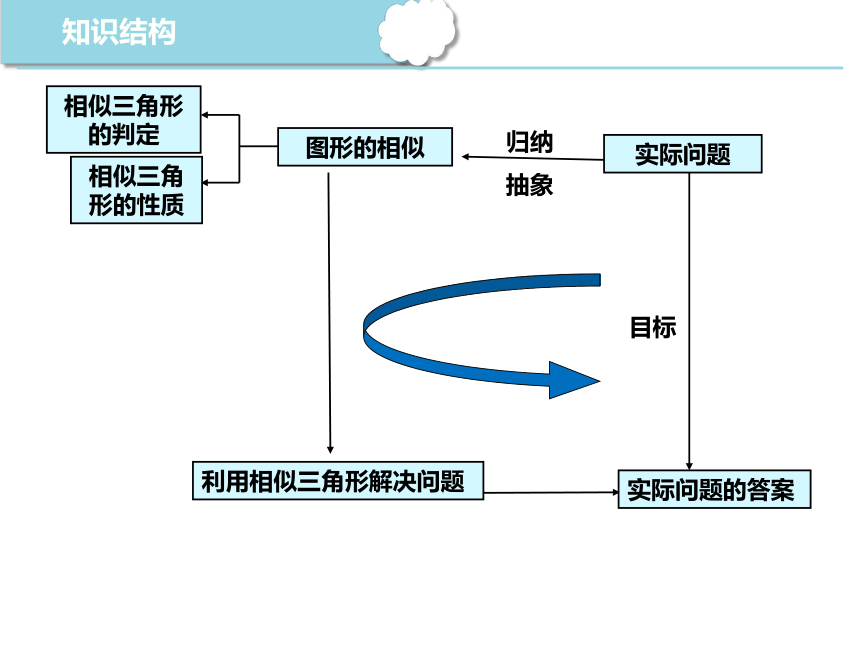
知识结构
归纳
抽象
图形的相似
利用相似三角形解决问题
实际问题
实际问题的答案
目标
相似三角形的判定
相似三角形的性质
6.1 图上距离与实际距离
一、比例的项:
在比例式a:b=c:d (即= )中,a,d称为比例外项,b,c称为比例内项.
特别地,在比例式(即)中,b称为a,c的比例中项,满足.
二、比例线段:
若 a、b、c、d 为四条线段 ,如果 = (或a:b=c:d),那么这四条线段a、b、 c 、 d 叫做成比例的线段,简称比例线段.
6.1 图上距离与实际距离
三、比的性质:
1.基本性质:若= ,那么
2.合比性质:若= ,那么=
3.分比性质:若= ,那么=
练习
1.已知,则( )
A. B. C. D.
答案:B
2.某机器零件在图纸上的长度是21mm,它的实际长度是630mm,则图纸的比例尺是( )
A.1∶20 B.1∶30
C.1∶40 D.1∶50
答案:B
6.2 黄金分割
黄金分割
若线段AB上一点C,把线段AB分成两条线段AC和BC(),且使AC是AB和BC的比例中项(即),则称线段AB被点C黄金分割,点C叫线段AB的黄金分割点.
其中, ,AC与AB的比叫做黄金比.
A
B
C
6.3 相似图形
一、相似三角形
定义:对应角相等、对应边成比例的三角形。
相似比:相似三角形的对应边的比,叫做相似三角形的相似比
二、相似多边形:
定义:对应角相等,对应边成比例的两个边数相等的多边形.
相似比:相似多边形对应边的比叫做相似比
6.4 探索三角形相似的条件
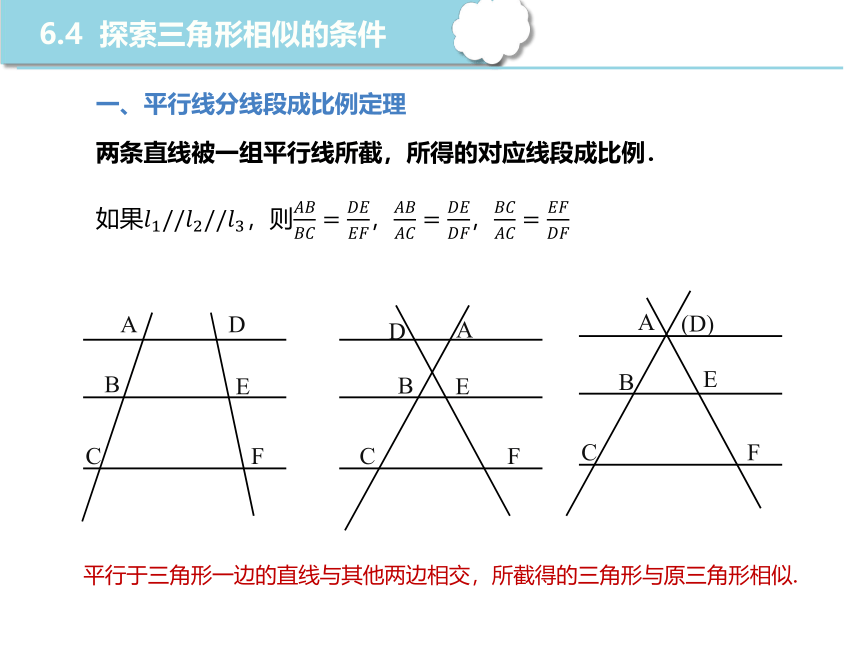
一、平行线分线段成比例定理
两条直线被一组平行线所截,所得的对应线段成比例.
如果,则,,
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
(D)
E
F
平行于三角形一边的直线与其他两边相交,所截得的三角形与原三角形相似.
6.4 探索三角形相似的条件
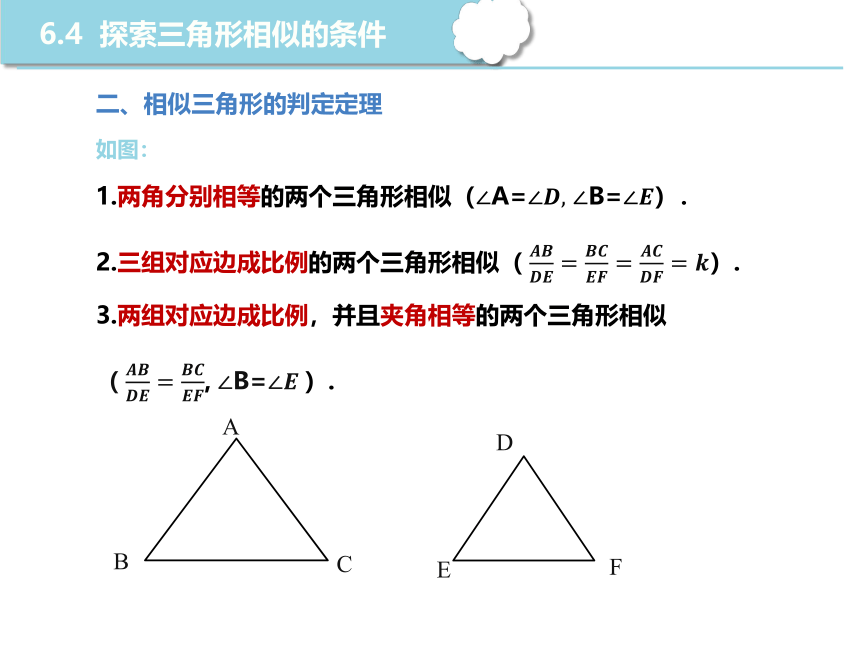
二、相似三角形的判定定理
如图:
1.两角分别相等的两个三角形相似(A= B=).
2.三组对应边成比例的两个三角形相似( ).
3.两组对应边成比例,并且夹角相等的两个三角形相似
( , B=).
A
B
C
D
E
F
练习
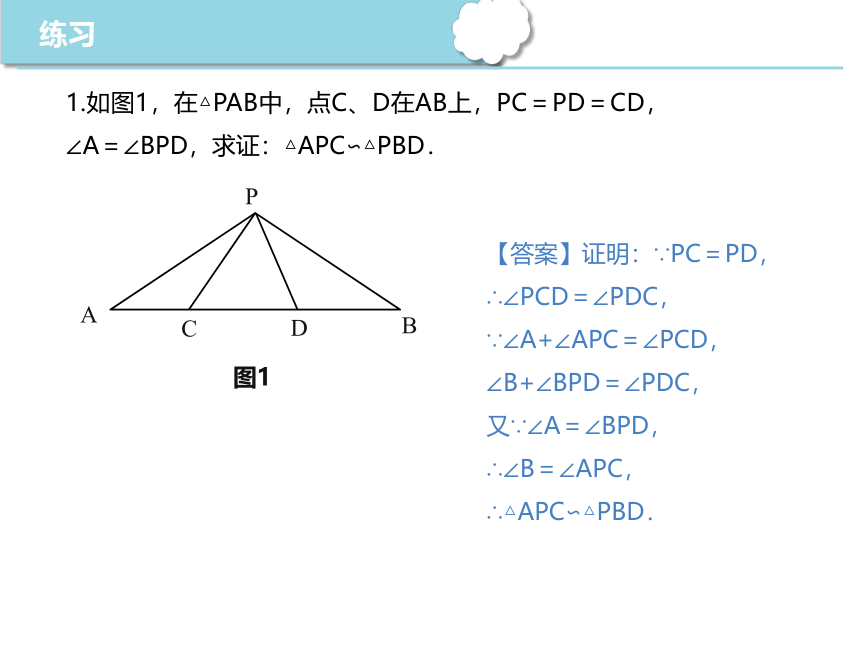
1.如图1,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△PBD.
P
A
C
D
B
图1
【答案】证明:∵PC=PD,
∴∠PCD=∠PDC,
∵∠A+∠APC=∠PCD,
∠B+∠BPD=∠PDC,
又∵∠A=∠BPD,
∴∠B=∠APC,
∴△APC∽△PBD.
练习
2.如图2,在矩形ABCD中,点E是BC边上的点,AC⊥DE,垂足为F.求证:△ABC∽△ECD.
D
C
B
A
F
图2
【答案】
证明:∵四边形ABCD是矩形,
∴∠B=∠BCD=90°.
∴∠ACB+∠ACD=90°.
又∵AC⊥DE,
∴∠CDE+∠ACD=90°.
∴∠ACB=∠CDE.
∴△ABC∽△ECD.
练习
3.如图,在和中,分别是上一点,.当时,判断与是否相似,并说明理由.
练习
【答案】解:相似,理由如下:
∵.
∴,
又∵,
∴,
∴△ADC∽△A′D′C′,
∴∠A=∠A′,
又∵,
∴△ABC∽△A′B′C′.
练习
4.如图,在△ABC中,点D、E分别在AB、AC上,DE、BC的延长线相交于点F,且EF DF=CF BF.求证:△CAB∽△DAE.
E
F
C
B
D
A
【答案】
证明:∵EF DF=CF BF.
∴,
∵∠EFC=∠BFD,
∴△EFC∽△BFD,
∴∠CEF=∠B,
∴∠B=∠AED,
∵∠CAB=∠DAE,
∴△CAB∽△DAE.
6.5 相似三角形的性质
相似三角形的性质
1.相似三角形的对应角相等.
(A= B=,)
2.相似三角形的对应边成比例
().
A
B
C
D
E
F
6.5 相似三角形的性质
相似三角形的性质
3.相似三角形的对应边上的中线,高线和对应角的平分线成比例,都等于相似比.
为中线,
C
M
L
L
6.5 相似三角形的性质
相似三角形的性质
4.相似三角形周长的比等于相似比.
6.5 相似三角形的性质
相似三角形的性质
4.相似三角形面积的比等于相似比的平方.
L
L
练习
1.图1,已知CD是Rt△ABC斜边上的高,则下列各式中不正确的是( )
A.BC2=BD AB B.CD2=BD AD
C.AC2=AD AB D.BC AD=AC BD
【答案】D
2.如图2,在矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F.若AB=4,BC=6,则DF的长为 .
L
图1
E
A
B
C
D
F
L
L
图2
3.如图,△OAB∽△OCD,OA:OC=3:2.△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2.则下列说法正确的是( )A. B. C. D.
【答案】C
∵△OAB∽△OCD,OA:OC=3:2,
∴,()2
选项C正确,选项D错误
练习
A
B
C
D
O
一、位似多边形
如果两个相似多边形任意一组对应顶点所在的直线都经过同一个点O,且每组对应点与点O 点的距离之比都等于一个定值k,如下图,OA′=k·OA(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.
6.6 图形的位似
二、位似图形的性质:
位似图形的对应点相交于同一点,此点就是位似中心;
位似图形的对应点到位似中心的距离之比等于相似比;
位似图形中不经过位似中心的对应线段平行.
6.6 图形的位似
三、作位似图形的步骤:
1.在原图上找若干个关键点,并任取一点作为位似中心;
2.作位似中心与各关键点连线;
3.在连线上取关键点的对应点,使之满足放缩比例;
4.顺次连接各对应点.
6.6 图形的位似
1.如图, △ABC 与 △DEF是位似图形,点 P和点 P是对应点,则 △ABC内的点 P(m,n)的对应点 P的坐标为( )
A.(2m,2n) B. (-2m,-2n) C.(2m,-2n) D.(-2m,2n)
【答案】B
练习
·
·
P
P
B
A
C
D
E
F
2.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且面积比为1:9,点A、B、E点在x轴上,若点D的坐标为(1,2),则点G的坐标为( )
A.(3,6) B.(4,8) C.(6,12) D.(6,10)
【答案】A
练习
一、平行投影
1.平行光的照射下,物体所产生的影.
(1)等高的物体垂直地面放置,在太阳光下,它们的影子一样长(图1).
(2)等长的物体平行于地面放置时,在太阳光下的影子一样长
且影长=物体本身的长度(图2 ).
6.7 用相似三角形解决问题
2.物高与影长的关系
(1)在不同时刻,同一物体的影子的方向和大小可能不同.
(2)在同一时刻,不同物体的物高与影长成正比例:
=.
注意:利用影长计算物高时,要注意的是测量两物体在同一时刻的影长.
6.7 用相似三角形解决问题
二、中心投影
在点光源的照射下,物体所产生的影称为中心投影.
(1)等高的物体垂直地面放置时,离点光源近的物体它的影子短,离点光源远的物体它的影子长(图1).
(2)等长的物体平行于地面放置时,一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短(图2).
6.7 用相似三角形解决问题
三、相似三角形的应用
1.测量高度
测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.
6.7 用相似三角形解决问题
三、相似三角形的应用
2.测量距离
1.如甲图所示,通常可先测量图中的线段DC、BD、CE的距离(长度),根据相似三角形的性质,求出AB的长.
2.如乙图所示,可先测AC、DC及DE的长,再根据相似三角形的性质计算AB的长.
6.7 用相似三角形解决问题
1.如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m,已知小明的身高是1.6 m,他的影长是2 m.
(1)图中△ABC与△ADE是否相似 为什么
(2)求古塔的高度
【答案】(1)△ABC∽△ADE.
∵BC⊥AE,DE⊥AE,∴∠ACB=∠AED=90°
∵∠A=∠A,∴△ABC∽△ADE
(2)由(1)得△ABC∽△ADE
∴ =
∵AC=2m,AE=2+18=20m,BC=1.6m,
∴ = ∴DE=16m
6.7 用相似三角形解决问题
2.某同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立 米长的标杆测得其影厂为 米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为 米和 米,则学校旗杆的高度为( )米.
8 B. 11.6 C. 1.2 D. 10
【答案】D
6.7 用相似三角形解决问题
3.如图,路灯灯柱OP的长为9米,身高1.8米的小明从距离路灯的底部(点O)20米的点A处,沿AO所在的直线行走14米到点B处时,人影的长度( )
A.变长了1.5米 B.变短了2.5米
C.变长了3.5米 D.变短了3.5米
【答案】D
6.7 用相似三角形解决问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
图形的相似
苏教版九年级下册
图形的相似
制作:没烦恼
6.6 图形的位似
6.7 用相似三角形解决问题
6.1 图上距离与实际距离
6.2 黄金分割
6.3 相似图形
6.4 探索三角形相似的条件
6.5 相似三角形的性质
CONTENTS
目录
知识结构
归纳
抽象
图形的相似
利用相似三角形解决问题
实际问题
实际问题的答案
目标
相似三角形的判定
相似三角形的性质
6.1 图上距离与实际距离
一、比例的项:
在比例式a:b=c:d (即= )中,a,d称为比例外项,b,c称为比例内项.
特别地,在比例式(即)中,b称为a,c的比例中项,满足.
二、比例线段:
若 a、b、c、d 为四条线段 ,如果 = (或a:b=c:d),那么这四条线段a、b、 c 、 d 叫做成比例的线段,简称比例线段.
6.1 图上距离与实际距离
三、比的性质:
1.基本性质:若= ,那么
2.合比性质:若= ,那么=
3.分比性质:若= ,那么=
练习
1.已知,则( )
A. B. C. D.
答案:B
2.某机器零件在图纸上的长度是21mm,它的实际长度是630mm,则图纸的比例尺是( )
A.1∶20 B.1∶30
C.1∶40 D.1∶50
答案:B
6.2 黄金分割
黄金分割
若线段AB上一点C,把线段AB分成两条线段AC和BC(),且使AC是AB和BC的比例中项(即),则称线段AB被点C黄金分割,点C叫线段AB的黄金分割点.
其中, ,AC与AB的比叫做黄金比.
A
B
C
6.3 相似图形
一、相似三角形
定义:对应角相等、对应边成比例的三角形。
相似比:相似三角形的对应边的比,叫做相似三角形的相似比
二、相似多边形:
定义:对应角相等,对应边成比例的两个边数相等的多边形.
相似比:相似多边形对应边的比叫做相似比
6.4 探索三角形相似的条件
一、平行线分线段成比例定理
两条直线被一组平行线所截,所得的对应线段成比例.
如果,则,,
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
(D)
E
F
平行于三角形一边的直线与其他两边相交,所截得的三角形与原三角形相似.
6.4 探索三角形相似的条件
二、相似三角形的判定定理
如图:
1.两角分别相等的两个三角形相似(A= B=).
2.三组对应边成比例的两个三角形相似( ).
3.两组对应边成比例,并且夹角相等的两个三角形相似
( , B=).
A
B
C
D
E
F
练习
1.如图1,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△PBD.
P
A
C
D
B
图1
【答案】证明:∵PC=PD,
∴∠PCD=∠PDC,
∵∠A+∠APC=∠PCD,
∠B+∠BPD=∠PDC,
又∵∠A=∠BPD,
∴∠B=∠APC,
∴△APC∽△PBD.
练习
2.如图2,在矩形ABCD中,点E是BC边上的点,AC⊥DE,垂足为F.求证:△ABC∽△ECD.
D
C
B
A
F
图2
【答案】
证明:∵四边形ABCD是矩形,
∴∠B=∠BCD=90°.
∴∠ACB+∠ACD=90°.
又∵AC⊥DE,
∴∠CDE+∠ACD=90°.
∴∠ACB=∠CDE.
∴△ABC∽△ECD.
练习
3.如图,在和中,分别是上一点,.当时,判断与是否相似,并说明理由.
练习
【答案】解:相似,理由如下:
∵.
∴,
又∵,
∴,
∴△ADC∽△A′D′C′,
∴∠A=∠A′,
又∵,
∴△ABC∽△A′B′C′.
练习
4.如图,在△ABC中,点D、E分别在AB、AC上,DE、BC的延长线相交于点F,且EF DF=CF BF.求证:△CAB∽△DAE.
E
F
C
B
D
A
【答案】
证明:∵EF DF=CF BF.
∴,
∵∠EFC=∠BFD,
∴△EFC∽△BFD,
∴∠CEF=∠B,
∴∠B=∠AED,
∵∠CAB=∠DAE,
∴△CAB∽△DAE.
6.5 相似三角形的性质
相似三角形的性质
1.相似三角形的对应角相等.
(A= B=,)
2.相似三角形的对应边成比例
().
A
B
C
D
E
F
6.5 相似三角形的性质
相似三角形的性质
3.相似三角形的对应边上的中线,高线和对应角的平分线成比例,都等于相似比.
为中线,
C
M
L
L
6.5 相似三角形的性质
相似三角形的性质
4.相似三角形周长的比等于相似比.
6.5 相似三角形的性质
相似三角形的性质
4.相似三角形面积的比等于相似比的平方.
L
L
练习
1.图1,已知CD是Rt△ABC斜边上的高,则下列各式中不正确的是( )
A.BC2=BD AB B.CD2=BD AD
C.AC2=AD AB D.BC AD=AC BD
【答案】D
2.如图2,在矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F.若AB=4,BC=6,则DF的长为 .
L
图1
E
A
B
C
D
F
L
L
图2
3.如图,△OAB∽△OCD,OA:OC=3:2.△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2.则下列说法正确的是( )A. B. C. D.
【答案】C
∵△OAB∽△OCD,OA:OC=3:2,
∴,()2
选项C正确,选项D错误
练习
A
B
C
D
O
一、位似多边形
如果两个相似多边形任意一组对应顶点所在的直线都经过同一个点O,且每组对应点与点O 点的距离之比都等于一个定值k,如下图,OA′=k·OA(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.
6.6 图形的位似
二、位似图形的性质:
位似图形的对应点相交于同一点,此点就是位似中心;
位似图形的对应点到位似中心的距离之比等于相似比;
位似图形中不经过位似中心的对应线段平行.
6.6 图形的位似
三、作位似图形的步骤:
1.在原图上找若干个关键点,并任取一点作为位似中心;
2.作位似中心与各关键点连线;
3.在连线上取关键点的对应点,使之满足放缩比例;
4.顺次连接各对应点.
6.6 图形的位似
1.如图, △ABC 与 △DEF是位似图形,点 P和点 P是对应点,则 △ABC内的点 P(m,n)的对应点 P的坐标为( )
A.(2m,2n) B. (-2m,-2n) C.(2m,-2n) D.(-2m,2n)
【答案】B
练习
·
·
P
P
B
A
C
D
E
F
2.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且面积比为1:9,点A、B、E点在x轴上,若点D的坐标为(1,2),则点G的坐标为( )
A.(3,6) B.(4,8) C.(6,12) D.(6,10)
【答案】A
练习
一、平行投影
1.平行光的照射下,物体所产生的影.
(1)等高的物体垂直地面放置,在太阳光下,它们的影子一样长(图1).
(2)等长的物体平行于地面放置时,在太阳光下的影子一样长
且影长=物体本身的长度(图2 ).
6.7 用相似三角形解决问题
2.物高与影长的关系
(1)在不同时刻,同一物体的影子的方向和大小可能不同.
(2)在同一时刻,不同物体的物高与影长成正比例:
=.
注意:利用影长计算物高时,要注意的是测量两物体在同一时刻的影长.
6.7 用相似三角形解决问题
二、中心投影
在点光源的照射下,物体所产生的影称为中心投影.
(1)等高的物体垂直地面放置时,离点光源近的物体它的影子短,离点光源远的物体它的影子长(图1).
(2)等长的物体平行于地面放置时,一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短(图2).
6.7 用相似三角形解决问题
三、相似三角形的应用
1.测量高度
测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.
6.7 用相似三角形解决问题
三、相似三角形的应用
2.测量距离
1.如甲图所示,通常可先测量图中的线段DC、BD、CE的距离(长度),根据相似三角形的性质,求出AB的长.
2.如乙图所示,可先测AC、DC及DE的长,再根据相似三角形的性质计算AB的长.
6.7 用相似三角形解决问题
1.如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m,已知小明的身高是1.6 m,他的影长是2 m.
(1)图中△ABC与△ADE是否相似 为什么
(2)求古塔的高度
【答案】(1)△ABC∽△ADE.
∵BC⊥AE,DE⊥AE,∴∠ACB=∠AED=90°
∵∠A=∠A,∴△ABC∽△ADE
(2)由(1)得△ABC∽△ADE
∴ =
∵AC=2m,AE=2+18=20m,BC=1.6m,
∴ = ∴DE=16m
6.7 用相似三角形解决问题
2.某同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立 米长的标杆测得其影厂为 米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为 米和 米,则学校旗杆的高度为( )米.
8 B. 11.6 C. 1.2 D. 10
【答案】D
6.7 用相似三角形解决问题
3.如图,路灯灯柱OP的长为9米,身高1.8米的小明从距离路灯的底部(点O)20米的点A处,沿AO所在的直线行走14米到点B处时,人影的长度( )
A.变长了1.5米 B.变短了2.5米
C.变长了3.5米 D.变短了3.5米
【答案】D
6.7 用相似三角形解决问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
