2023-2024学年高中物理人教版(2019)必修第一册课后习题 第4章 习题课:用牛顿运动定律解决几类问题(含答案)
文档属性
| 名称 | 2023-2024学年高中物理人教版(2019)必修第一册课后习题 第4章 习题课:用牛顿运动定律解决几类问题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 353.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览

文档简介
习题课:用牛顿运动定律解决几类问题
必备知识基础练
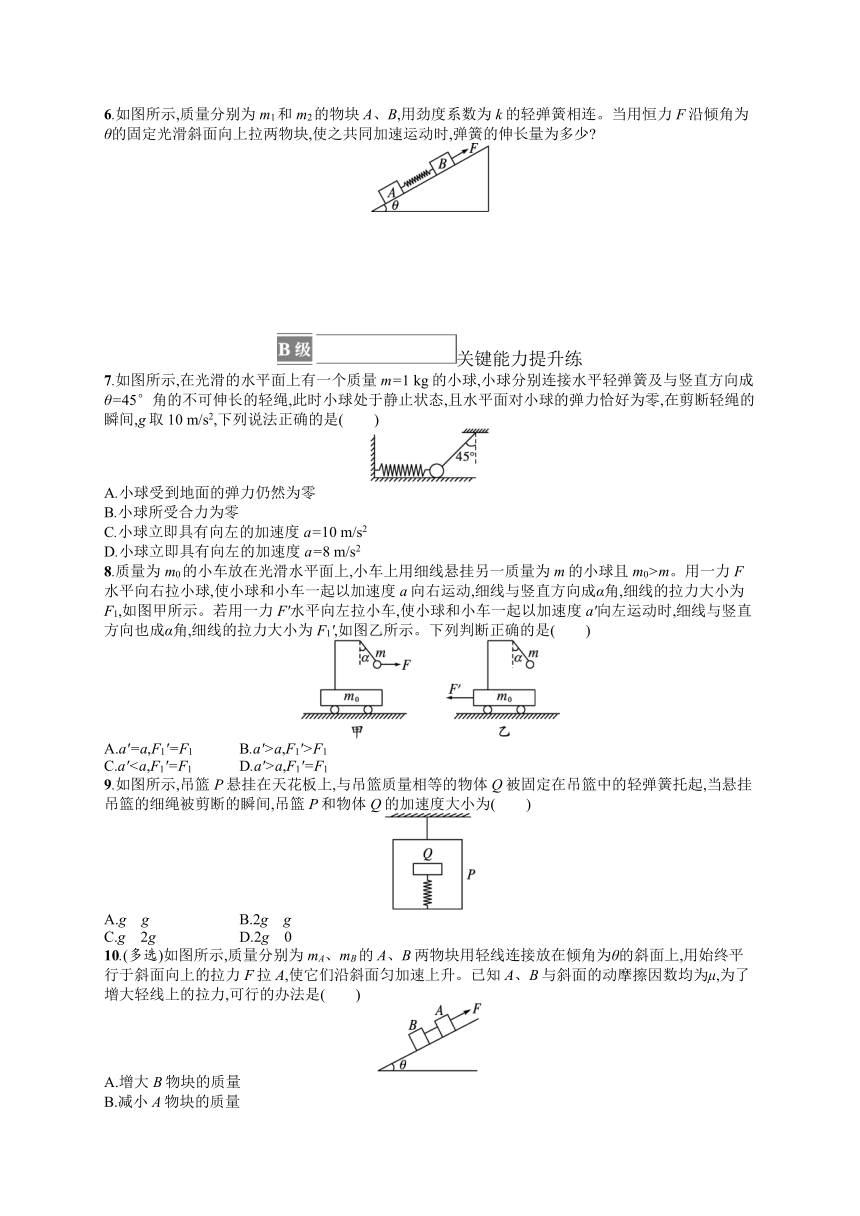
1.(多选)(2022湖北武汉高一期末)如图所示,质量为m的开孔小球,套在与水平面成45°角、固定的光滑杆OA上,小球被水平绳拉着处于静止状态。现剪断绳子,下列说法正确的是(已知重力加速度为g)( )
A.剪断绳子前绳子拉力大小为mg
B.剪断绳子后OA杆对球的作用力大小为mg
C.剪断绳子后球的加速度大小为g
D.剪断绳子后球的加速度大小为g
2.(多选)如图所示,铁球A和铁块B之间由弹簧相连,并用细线OA挂在天花板上,A、B的质量分别为m和2m,弹簧的劲度系数为k,整个系统静止,下述说法正确的是( )
A.细线对铁球A的拉力大小为mg
B.弹簧的长度为
C.弹簧的弹力大小为2mg
D.某时刻烧断细绳OA,该时刻铁球A的加速度大小为3g
3.在太空中可以采用动力学方法测量物体的质量,其原理如图所示。在太空舱中将质量为m1的标准物体A与质量为m2的待测物体B紧靠在一起,施加一水平推力F=200 N后,在观测时间Δt=0.02 s内,标准物体A和待测物体B的速度变化是0.4 m/s,若已知标准物体A的质量为2.0 kg,则待测物体B的质量为( )
A.3.0 kg B.8.0 kg
C.10.0 kg D.98.0 kg
4.如图所示,质量为2m的物块A与水平地面间的动摩擦因数为μ,质量为m的物块B与水平地面的摩擦不计,在大小为F的水平推力作用下,A、B一起向右做加速运动,则A和B之间的作用力大小为( )
A. B.
C. D.
5.如图所示,A、B两物块的质量分别为m和m0,使它们一起从光滑斜面的顶端由静止开始下滑;已知斜面的倾角为θ,斜面始终保持静止。则在此过程中物块B对物块A的压力为( )
A.m0gsin θ B.m0gcos θ
C.0 D.(m0+m)gsin θ
6.如图所示,质量分别为m1和m2的物块A、B,用劲度系数为k的轻弹簧相连。当用恒力F沿倾角为θ的固定光滑斜面向上拉两物块,使之共同加速运动时,弹簧的伸长量为多少
关键能力提升练
7.如图所示,在光滑的水平面上有一个质量m=1 kg的小球,小球分别连接水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳,此时小球处于静止状态,且水平面对小球的弹力恰好为零,在剪断轻绳的瞬间,g取10 m/s2,下列说法正确的是( )
A.小球受到地面的弹力仍然为零
B.小球所受合力为零
C.小球立即具有向左的加速度a=10 m/s2
D.小球立即具有向左的加速度a=8 m/s2
8.质量为m0的小车放在光滑水平面上,小车上用细线悬挂另一质量为m的小球且m0>m。用一力F水平向右拉小球,使小球和小车一起以加速度a向右运动,细线与竖直方向成α角,细线的拉力大小为F1,如图甲所示。若用一力F'水平向左拉小车,使小球和小车一起以加速度a'向左运动时,细线与竖直方向也成α角,细线的拉力大小为F1',如图乙所示。下列判断正确的是( )
A.a'=a,F1'=F1 B.a'>a,F1'>F1
C.a'a,F1'=F1
9.如图所示,吊篮P悬挂在天花板上,与吊篮质量相等的物体Q被固定在吊篮中的轻弹簧托起,当悬挂吊篮的细绳被剪断的瞬间,吊篮P和物体Q的加速度大小为( )
A.g g B.2g g
C.g 2g D.2g 0
10.(多选)如图所示,质量分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的拉力F拉A,使它们沿斜面匀加速上升。已知A、B与斜面的动摩擦因数均为μ,为了增大轻线上的拉力,可行的办法是( )
A.增大B物块的质量
B.减小A物块的质量
C.增大倾角θ
D.增大动摩擦因数μ
11.如图所示,滑块m和质量为2 kg的木板m0叠在一起,静止在光滑的水平地面上,两者间的动摩擦因数μ=0.2。现给木板施加水平向右的恒力F=8 N,为使木板与滑块在其后的运动中始终保持相对静止,滑块m的质量可能为( )
A.2.2 kg B.1.8 kg
C.1.2 kg D.0.6 kg
12.如图所示,质量均为3 kg的物块A与物块B紧挨着并排放在光滑水平面上,A、B间接触面垂直于纸面且与水平面的夹角θ=45°,A、B接触面光滑无摩擦,开始时A、B都静止,现施加一水平推力F,使A、B一起向右加速运动,g取10 m/s2,试求:
(1)若F=12 N,使A、B一起向右加速且不发生相对滑动,A、B共同运动的加速度大小;
(2)要使A、B发生相对滑动,水平推力至少为多大以及此时的加速度大小。
13.如图所示,一同学用长为l=1.5 m的细绳AB拉质量m=15.6 kg的箱子,当B端距地面高度h=0.9 m,绳间拉力F=60 N时,箱子刚好沿水平地面做匀速直线运动。已知=1.08,重力加速度g取10 m/s2。
(1)求箱子与地面间的动摩擦因数μ;
(2)若要以最小的力拉B端,使箱子以0.5 m/s2的加速度向右做匀加速直线运动,求拉力的最小值。
习题课:用牛顿运动定律解决几类问题
1.AD 对小球受力分析如图所示,剪断绳子前绳子拉力大小为F=mgtan 45°=mg,选项A正确;剪断绳子后OA杆对球的作用力大小为FN=mgcos 45°=mg,选项B错误;剪断绳子后球的加速度大小为a=g,选项C错误,D正确。
2.CD 将A、B看成整体,根据平衡条件可知FT=(m+2m)g=3mg,故选项A错误;设弹簧的伸长量为x,则对B物块根据胡克定律可知kx=2mg,则x=,弹簧的长度为原长与伸长量之和,故选项B错误,C正确;某时刻烧断细线OA,则细线对A的拉力立刻为零,则A受到本身的重力以及弹簧的弹力作用,根据牛顿第二定律有,mg+kx=ma,kx=2mg,联立可以得到a=3g,故选项D正确。
3.B 整体运动的加速度为a= m/s2=20 m/s2,由牛顿第二定律F=(m1+m2)a,解得m2=8.0 kg,故选B。
4.D 以A、B组成的系统为研究对象,由牛顿第二定律得系统的加速度a=,以B为研究对象,由牛顿第二定律得A对B的作用力:FAB=ma=,D正确。
5.C 对A、B组成的系统整体受力分析可知,整体受重力、支持力而做匀加速直线运动;由牛顿第二定律可知,a==gsin θ,再对A受力分析,设B对A的压力为F,由牛顿第二定律可知mgsin θ+F=ma,解得F=0,说明A、B间没有作用力,则C正确。
6.解析 对整体分析得:F-(m1+m2)gsin θ=(m1+m2)a ①
隔离A得:kx-m1gsin θ=m1a ②
联立①②得x=。
答案
7.C 剪断细线前,小球在重力、细线的拉力和弹簧拉力作用下处于静止状态,三力的合力为零,由此可知弹簧的弹力大小等于小球的重力大小。剪断细线的瞬间,弹簧的弹力不变,细线的拉力消失,此时小球和地面之间的弹力瞬间增加,大小等于竖直方向的重力的大小,小球受到的合力为弹簧的弹力,即方向向左、大小为mg,故小球的加速度向左,且a=10 m/s2。
8.D 先对题图甲中的整体受力分析,受重力、支持力和拉力,根据牛顿第二定律,有F=(m0+m)a,再隔离题图甲中的小球受力分析,如图(a)所示。
根据牛顿第二定律,有F-F1 sin α=ma,F1cos α-mg=0,联立以上三式解得F1=,a=。再隔离题图乙中小球受力分析,如图(b)所示。由几何关系得F合=mgtan α,F1'=,由牛顿第二定律,得a'=gtan α,由于m0>m,故a'>a,F1'=F1,故D正确。
9.D 剪断细线前,对P、Q整体受力分析,受到总重力和细线的拉力而平衡,故FT=2mg;再对物体Q受力分析,受到重力、弹簧的支持力;剪断细线后,重力和弹簧的弹力不变,细线的拉力减为零,故物体P受到的力的合力等于2mg,方向向下,所以aP=2g,物体Q受到的力不变,合力为零,所以aQ=0,故选项D正确,A、B、C错误。
10.AB 设轻线的张力为FT,则对B分析有FT-mBgsin θ-μmBgcos θ=mBa
对整体分析:F-(mB+mA)gsin θ-μ(mB+mA)gcos θ=(mB+mA)a
解得FT=。增大B物块的质量,由上式可知,拉力FT增大,A正确;
减小A物块的质量,拉力FT增大,B正确;拉力FT与倾角θ无关,C错误;拉力FT与动摩擦因数μ无关,D错误。
11.A 设滑块的最大加速度为a,对滑块由牛顿第二定律有μmg=ma
可得a=2 m/s2,木板与滑块在运动中始终保持相对静止,对系统有F≤(m0+m)a
解得m≥2 kg,故选A。
12.解析 (1)A、B一起向右加速且不发生相对滑动,以A、B为整体受力分析可得
F=2ma
得A、B共同运动的加速度大小a=2 m/s2。
(2)设A、B间的弹力为FN,推力F越大,则A越可能相对于B向上滑,当F最大时,A刚要相对B向上滑,A不受水平面的支持力,设此时A、B共同以加速度a1沿水平面加速前进,对A由牛顿第二定律得F-FNsin 45°=ma1,FNcos 45°=mg
对B由牛顿第二定律得FNsin 45°=ma1,联立上式解得F=60 N,a1=10 m/s2
即A、B刚发生相对滑动的水平推力至少为60 N,加速度大小为10 m/s2。
答案 (1)2 m/s2 (2)60 N 10 m/s2
13.解析 (1)对箱子受力分析,如图所示
因箱子做匀速直线运动,故箱子受力平衡,
所以FTcos θ=μ(mg-FTsin θ)
由几何关系可知sin θ=0.6,cos θ=0.8
代入数据解得μ=0.4。
(2)箱子向右做匀加速直线运动,
所以FTcos θ-μ(mg-FTsin θ)=ma
化简得FT=
令tan β=μ
整理得FT=
所以θ=β时,FT取最小值
即FTmin==65 N。
必备知识基础练
1.(多选)(2022湖北武汉高一期末)如图所示,质量为m的开孔小球,套在与水平面成45°角、固定的光滑杆OA上,小球被水平绳拉着处于静止状态。现剪断绳子,下列说法正确的是(已知重力加速度为g)( )
A.剪断绳子前绳子拉力大小为mg
B.剪断绳子后OA杆对球的作用力大小为mg
C.剪断绳子后球的加速度大小为g
D.剪断绳子后球的加速度大小为g
2.(多选)如图所示,铁球A和铁块B之间由弹簧相连,并用细线OA挂在天花板上,A、B的质量分别为m和2m,弹簧的劲度系数为k,整个系统静止,下述说法正确的是( )
A.细线对铁球A的拉力大小为mg
B.弹簧的长度为
C.弹簧的弹力大小为2mg
D.某时刻烧断细绳OA,该时刻铁球A的加速度大小为3g
3.在太空中可以采用动力学方法测量物体的质量,其原理如图所示。在太空舱中将质量为m1的标准物体A与质量为m2的待测物体B紧靠在一起,施加一水平推力F=200 N后,在观测时间Δt=0.02 s内,标准物体A和待测物体B的速度变化是0.4 m/s,若已知标准物体A的质量为2.0 kg,则待测物体B的质量为( )
A.3.0 kg B.8.0 kg
C.10.0 kg D.98.0 kg
4.如图所示,质量为2m的物块A与水平地面间的动摩擦因数为μ,质量为m的物块B与水平地面的摩擦不计,在大小为F的水平推力作用下,A、B一起向右做加速运动,则A和B之间的作用力大小为( )
A. B.
C. D.
5.如图所示,A、B两物块的质量分别为m和m0,使它们一起从光滑斜面的顶端由静止开始下滑;已知斜面的倾角为θ,斜面始终保持静止。则在此过程中物块B对物块A的压力为( )
A.m0gsin θ B.m0gcos θ
C.0 D.(m0+m)gsin θ
6.如图所示,质量分别为m1和m2的物块A、B,用劲度系数为k的轻弹簧相连。当用恒力F沿倾角为θ的固定光滑斜面向上拉两物块,使之共同加速运动时,弹簧的伸长量为多少
关键能力提升练
7.如图所示,在光滑的水平面上有一个质量m=1 kg的小球,小球分别连接水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳,此时小球处于静止状态,且水平面对小球的弹力恰好为零,在剪断轻绳的瞬间,g取10 m/s2,下列说法正确的是( )
A.小球受到地面的弹力仍然为零
B.小球所受合力为零
C.小球立即具有向左的加速度a=10 m/s2
D.小球立即具有向左的加速度a=8 m/s2
8.质量为m0的小车放在光滑水平面上,小车上用细线悬挂另一质量为m的小球且m0>m。用一力F水平向右拉小球,使小球和小车一起以加速度a向右运动,细线与竖直方向成α角,细线的拉力大小为F1,如图甲所示。若用一力F'水平向左拉小车,使小球和小车一起以加速度a'向左运动时,细线与竖直方向也成α角,细线的拉力大小为F1',如图乙所示。下列判断正确的是( )
A.a'=a,F1'=F1 B.a'>a,F1'>F1
C.a'
9.如图所示,吊篮P悬挂在天花板上,与吊篮质量相等的物体Q被固定在吊篮中的轻弹簧托起,当悬挂吊篮的细绳被剪断的瞬间,吊篮P和物体Q的加速度大小为( )
A.g g B.2g g
C.g 2g D.2g 0
10.(多选)如图所示,质量分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的拉力F拉A,使它们沿斜面匀加速上升。已知A、B与斜面的动摩擦因数均为μ,为了增大轻线上的拉力,可行的办法是( )
A.增大B物块的质量
B.减小A物块的质量
C.增大倾角θ
D.增大动摩擦因数μ
11.如图所示,滑块m和质量为2 kg的木板m0叠在一起,静止在光滑的水平地面上,两者间的动摩擦因数μ=0.2。现给木板施加水平向右的恒力F=8 N,为使木板与滑块在其后的运动中始终保持相对静止,滑块m的质量可能为( )
A.2.2 kg B.1.8 kg
C.1.2 kg D.0.6 kg
12.如图所示,质量均为3 kg的物块A与物块B紧挨着并排放在光滑水平面上,A、B间接触面垂直于纸面且与水平面的夹角θ=45°,A、B接触面光滑无摩擦,开始时A、B都静止,现施加一水平推力F,使A、B一起向右加速运动,g取10 m/s2,试求:
(1)若F=12 N,使A、B一起向右加速且不发生相对滑动,A、B共同运动的加速度大小;
(2)要使A、B发生相对滑动,水平推力至少为多大以及此时的加速度大小。
13.如图所示,一同学用长为l=1.5 m的细绳AB拉质量m=15.6 kg的箱子,当B端距地面高度h=0.9 m,绳间拉力F=60 N时,箱子刚好沿水平地面做匀速直线运动。已知=1.08,重力加速度g取10 m/s2。
(1)求箱子与地面间的动摩擦因数μ;
(2)若要以最小的力拉B端,使箱子以0.5 m/s2的加速度向右做匀加速直线运动,求拉力的最小值。
习题课:用牛顿运动定律解决几类问题
1.AD 对小球受力分析如图所示,剪断绳子前绳子拉力大小为F=mgtan 45°=mg,选项A正确;剪断绳子后OA杆对球的作用力大小为FN=mgcos 45°=mg,选项B错误;剪断绳子后球的加速度大小为a=g,选项C错误,D正确。
2.CD 将A、B看成整体,根据平衡条件可知FT=(m+2m)g=3mg,故选项A错误;设弹簧的伸长量为x,则对B物块根据胡克定律可知kx=2mg,则x=,弹簧的长度为原长与伸长量之和,故选项B错误,C正确;某时刻烧断细线OA,则细线对A的拉力立刻为零,则A受到本身的重力以及弹簧的弹力作用,根据牛顿第二定律有,mg+kx=ma,kx=2mg,联立可以得到a=3g,故选项D正确。
3.B 整体运动的加速度为a= m/s2=20 m/s2,由牛顿第二定律F=(m1+m2)a,解得m2=8.0 kg,故选B。
4.D 以A、B组成的系统为研究对象,由牛顿第二定律得系统的加速度a=,以B为研究对象,由牛顿第二定律得A对B的作用力:FAB=ma=,D正确。
5.C 对A、B组成的系统整体受力分析可知,整体受重力、支持力而做匀加速直线运动;由牛顿第二定律可知,a==gsin θ,再对A受力分析,设B对A的压力为F,由牛顿第二定律可知mgsin θ+F=ma,解得F=0,说明A、B间没有作用力,则C正确。
6.解析 对整体分析得:F-(m1+m2)gsin θ=(m1+m2)a ①
隔离A得:kx-m1gsin θ=m1a ②
联立①②得x=。
答案
7.C 剪断细线前,小球在重力、细线的拉力和弹簧拉力作用下处于静止状态,三力的合力为零,由此可知弹簧的弹力大小等于小球的重力大小。剪断细线的瞬间,弹簧的弹力不变,细线的拉力消失,此时小球和地面之间的弹力瞬间增加,大小等于竖直方向的重力的大小,小球受到的合力为弹簧的弹力,即方向向左、大小为mg,故小球的加速度向左,且a=10 m/s2。
8.D 先对题图甲中的整体受力分析,受重力、支持力和拉力,根据牛顿第二定律,有F=(m0+m)a,再隔离题图甲中的小球受力分析,如图(a)所示。
根据牛顿第二定律,有F-F1 sin α=ma,F1cos α-mg=0,联立以上三式解得F1=,a=。再隔离题图乙中小球受力分析,如图(b)所示。由几何关系得F合=mgtan α,F1'=,由牛顿第二定律,得a'=gtan α,由于m0>m,故a'>a,F1'=F1,故D正确。
9.D 剪断细线前,对P、Q整体受力分析,受到总重力和细线的拉力而平衡,故FT=2mg;再对物体Q受力分析,受到重力、弹簧的支持力;剪断细线后,重力和弹簧的弹力不变,细线的拉力减为零,故物体P受到的力的合力等于2mg,方向向下,所以aP=2g,物体Q受到的力不变,合力为零,所以aQ=0,故选项D正确,A、B、C错误。
10.AB 设轻线的张力为FT,则对B分析有FT-mBgsin θ-μmBgcos θ=mBa
对整体分析:F-(mB+mA)gsin θ-μ(mB+mA)gcos θ=(mB+mA)a
解得FT=。增大B物块的质量,由上式可知,拉力FT增大,A正确;
减小A物块的质量,拉力FT增大,B正确;拉力FT与倾角θ无关,C错误;拉力FT与动摩擦因数μ无关,D错误。
11.A 设滑块的最大加速度为a,对滑块由牛顿第二定律有μmg=ma
可得a=2 m/s2,木板与滑块在运动中始终保持相对静止,对系统有F≤(m0+m)a
解得m≥2 kg,故选A。
12.解析 (1)A、B一起向右加速且不发生相对滑动,以A、B为整体受力分析可得
F=2ma
得A、B共同运动的加速度大小a=2 m/s2。
(2)设A、B间的弹力为FN,推力F越大,则A越可能相对于B向上滑,当F最大时,A刚要相对B向上滑,A不受水平面的支持力,设此时A、B共同以加速度a1沿水平面加速前进,对A由牛顿第二定律得F-FNsin 45°=ma1,FNcos 45°=mg
对B由牛顿第二定律得FNsin 45°=ma1,联立上式解得F=60 N,a1=10 m/s2
即A、B刚发生相对滑动的水平推力至少为60 N,加速度大小为10 m/s2。
答案 (1)2 m/s2 (2)60 N 10 m/s2
13.解析 (1)对箱子受力分析,如图所示
因箱子做匀速直线运动,故箱子受力平衡,
所以FTcos θ=μ(mg-FTsin θ)
由几何关系可知sin θ=0.6,cos θ=0.8
代入数据解得μ=0.4。
(2)箱子向右做匀加速直线运动,
所以FTcos θ-μ(mg-FTsin θ)=ma
化简得FT=
令tan β=μ
整理得FT=
所以θ=β时,FT取最小值
即FTmin==65 N。
