期末复习-几何与统计五年级数学下册冀教版(含答案)
文档属性
| 名称 | 期末复习-几何与统计五年级数学下册冀教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 182.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 10:33:47 | ||
图片预览


文档简介
单专项复习素质评价
几何与统计
一、填空。(每空 1 分,共 20 分)
1.在括号里填上合适的单位或数。
一个学生大约每天喝水 1.2( )。
一个花盆的体积大约是 5( )。
680 dm3 =( )m3
0.4 L =( )mL
34 dm3 =( )cm3
1.5 L =( )dm3 =( )cm3
2.钟面上时针从数字 2 顺时针旋转 90°到达数字( ),然后再从这个位置顺时针旋转 90°到达数字( )。
3.把 60 升水倒入一个长 6 分米、宽 2.5 分米的长方体水箱内,正好倒满,这个水箱的高是( )分米。
4.有一个长方体玻璃缸,长 1 米,宽 8 分米,高 6 分米,里面水深 4.5 分米。如果在缸中投入一块棱长是 5 分米的正方体铁块,那么水将溢出( )升。
5.有一个长方体纸盒,从里面量得长 36 厘米、宽 12 厘米、高 5 厘米。把棱长为 5 厘米的正方体装入长方体纸盒内且正方体不能露出,最多能装( )个这样的正方体。
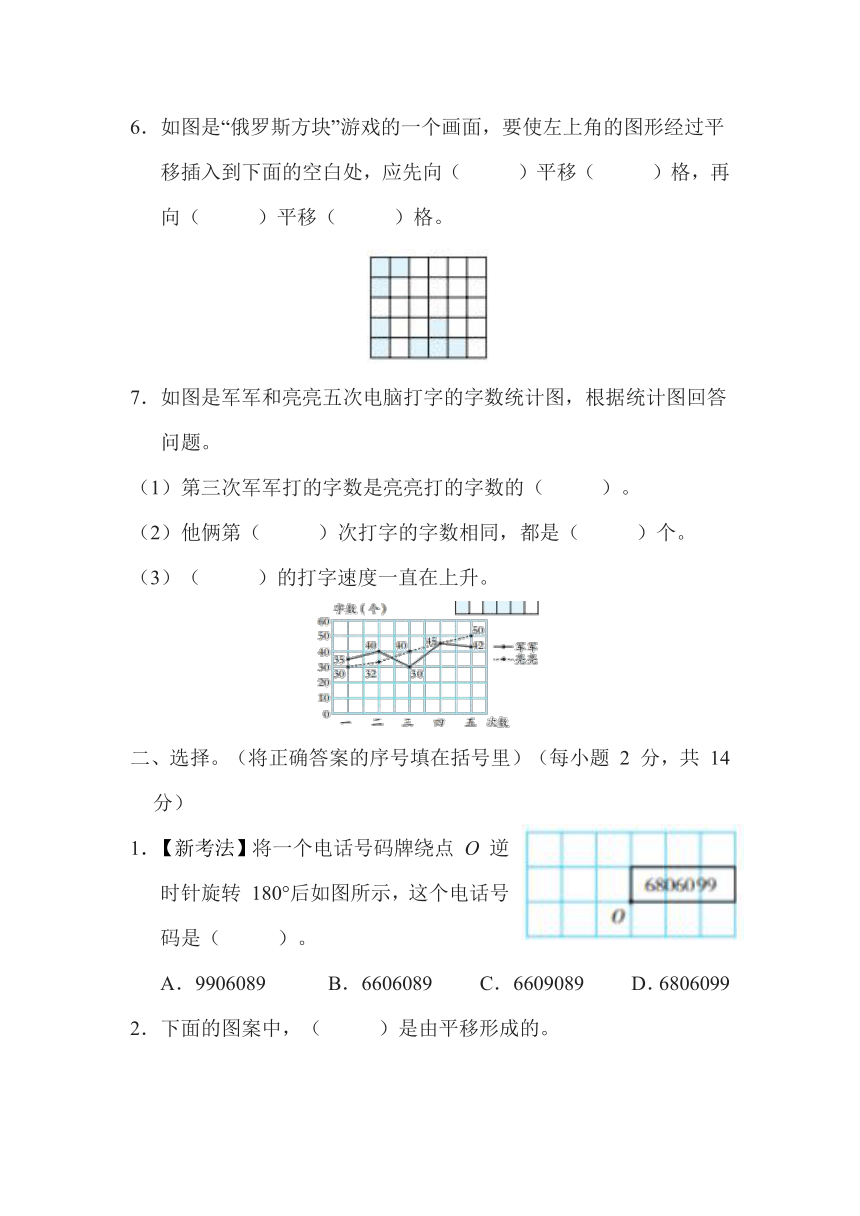
6.如图是“俄罗斯方块”游戏的一个画面,要使左上角的图形经过平移插入到下面的空白处,应先向( )平移( )格,再向( )平移( )格。
7.如图是军军和亮亮五次电脑打字的字数统计图,根据统计图回答问题。
(1)第三次军军打的字数是亮亮打的字数的( )。
(2)他俩第( )次打字的字数相同,都是( )个。
(3)( )的打字速度一直在上升。
二、选择。(将正确答案的序号填在括号里)(每小题 2 分,共 14 分)
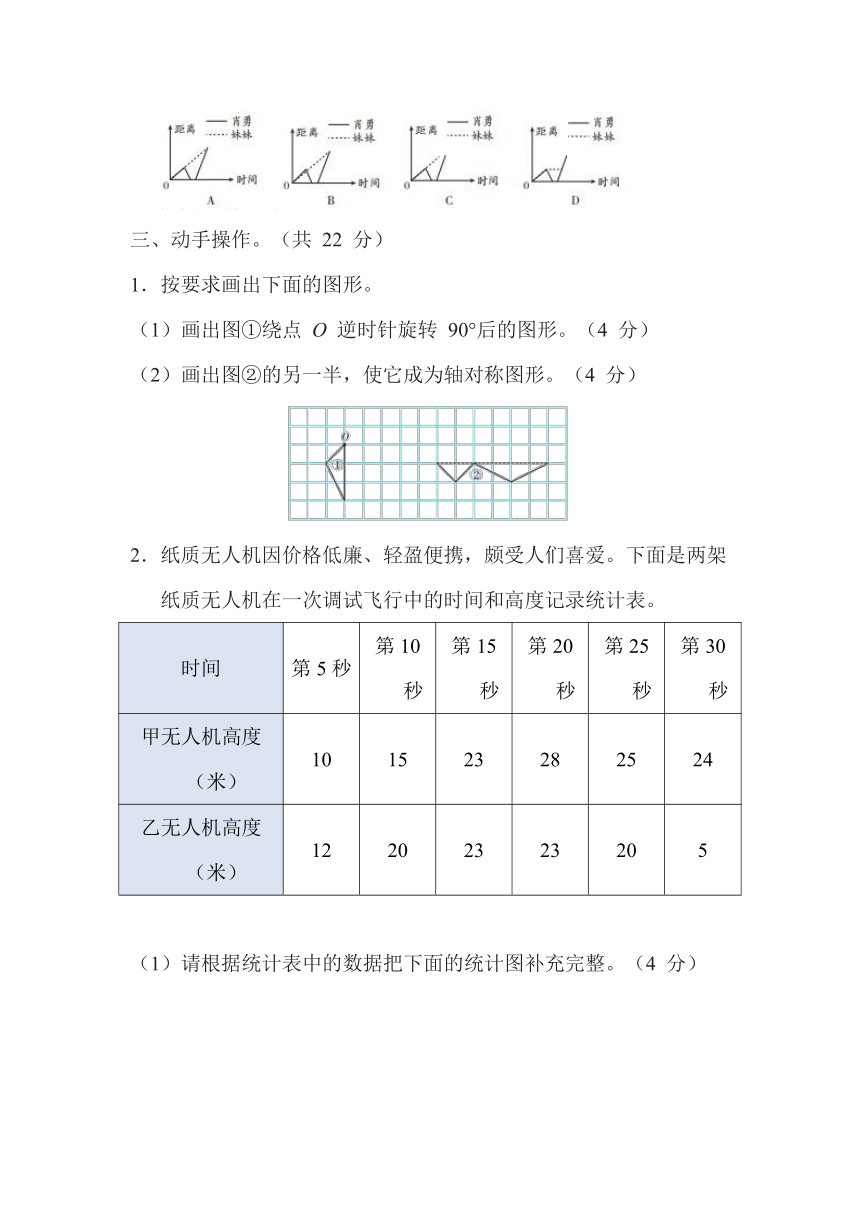
1.【新考法】将一个电话号码牌绕点 O 逆时针旋转 180°后如图所示,这个电话号码是( )。
A.9906089 B.6606089 C.6609089 D.6806099
2.下面的图案中,( )是由平移形成的。
3.同同想了解去年 12 月期间某市每天最高气温和最低气温的变化情况,她应该制作( )统计图。
A.单式条形 B.复式条形 C.单式折线 D.复式折线
4.下面的图形中,( )是轴对称图形。
5.一个大正方体的体积是小正方体的 8 倍,则这个大正方体的棱长之和是小正方体的棱长之和的( )倍。
A.2 B.4 C.6 D.8
6.【新题型】把10升水倒入一个长 2.5 分米、宽 20 厘米、高 5 分米的长方体水缸中。你能求出此时水面的高度吗?要解决这个问题,需要用到的信息有( )。
A.10 升、2.5 分米、20 厘米、5 分米
B.10 升、2.5 分米、20 厘米
C.2.5 分米、20 厘米、5 分米
D.10 升、20 厘米、5 分米
7.肖勇和妹妹一起去上学,途中肖勇发现忘带作业本了,于是他跑回家,拿上作业本, 马上向学校飞奔而去,刚好在学校门口追上了妹妹。下面四幅图中,( )描述的是肖勇和妹妹上学路上的情景。
三、动手操作。(共 22 分)
1.按要求画出下面的图形。
(1)画出图①绕点 O 逆时针旋转 90°后的图形。(4 分)
(2)画出图②的另一半,使它成为轴对称图形。(4 分)
2.纸质无人机因价格低廉、轻盈便携,颇受人们喜爱。下面是两架纸质无人机在一次调试飞行中的时间和高度记录统计表。
时间 第5秒 第10秒 第15秒 第20秒 第25秒 第30秒
甲无人机高度(米) 10 15 23 28 25 24
乙无人机高度(米) 12 20 23 23 20 5
(1)请根据统计表中的数据把下面的统计图补充完整。(4 分)
(2)从图上看,起飞后第( )秒两架无人机处于同一高度;起飞后第( )秒两架无人机的高度相差最大。(4 分)
(3)从起飞后第 15 秒至第 20 秒,甲无人机的飞行状态呈什么变化趋势?乙无人机的飞行状态呈什么变化趋势?(6 分)
四、解决问题。(共 44 分)
1.一件雕塑的底座是用混凝土浇筑成的长方体,它的高是 2.8 米,底面是边长为 2.5 米的正方形。这件雕塑的占地面积是多少平方米?浇筑这件雕塑的底座需要混凝土多少立方米?(8 分)
2.为了测出一块石头的体积,华华找来一个长 15 厘米、宽 10 厘米、足够高的长方体塑料盒子(如图),并倒入 10 厘米高的水,然后把石头浸没在水中,这时水面高 15 厘米。 这块石头的体积是多少立方厘米?(9 分)
3.挖一条长200米的水渠,水渠的横截面是一个梯形(如图)。一共要挖出多少立方米的土? (9 分)
4.【新情境】孔明灯,又叫天灯、许愿灯,是一种古老的手工艺品。在古代,孔明灯多用于军事方面;在现代,孔明灯多用来祈福。
(1)制作长方体孔明灯时,除了底面外,其他面都要糊上安全阻燃棉纸。制作一个如图所示的孔明灯,至少需要多少平方厘米的安全阻燃棉纸?(6 分)
(2)制作一个这样的孔明灯框架,至少需要多少厘米的竹条?(6 分)
(3)这个孔明灯的体积是多少立方厘米?(6 分)
★附加题:天才的你,试一试。(10 分)
一个长方体,如果长增加 2 厘米,宽和高不变,那么体积就增加 40 立方厘米;如果高增加 2 厘米,长和宽不变,那么体积就增加 60 立方厘米;如果宽增加 2 厘米,长和高不变,那么体积就增加 48 立方厘米。原来长方体的表面积是多少平方厘米?
答案
一、1.升 立方分米 0.68 400 34000
1.5 1500
2.5 8 3.4 4.5 5.14
6.右 1 下 3
7.(1)(2)四 45 (3)亮亮
二、1.C 2.A 3.D 4.B 5.A 6.B
7.A 【点拨】两人一开始一起去上学,所以速度一样,最后两人同时到校,所以 A 选项符合肖勇和妹妹上学路上的情景。
(2)15 30
(3)甲无人机一直上升,并在第 20 秒达到最大高度;乙无人机平稳飞行,高度没有发生变化。
四、1.2.5×2.5 = 6.25(平方米) 6.25×2.8 = 17.5(立方米)
答:这件雕塑的占地面积是 6.25 平方米。浇筑这件雕塑的底座需要混凝土 17.5 立方米。
2.15 - 10 = 5(厘米) 15×10×5 = 750(立方厘米)
答:这块石头的体积是 750 立方厘米。
3.(2 + 4)×2÷2×200 = 1200(立方米)
答:一共要挖出 1200 立方米的土。
4.(1)30×50×4 + 30×30 = 6900(平方厘米)
答:至少需要 6900 平方厘米的安全阻燃棉纸。
(2)(30 + 30 + 50)×4 = 440(厘米)
答:至少需要 440 厘米的竹条。
(3)30×30×50 = 45000(立方厘米)
答:这个孔明灯的体积是 45000 立方厘米。
附加题:宽 × 高 = 40÷2 = 20(平方厘米)
长 × 宽 = 60÷2 = 30(平方厘米)
长 × 高 = 48÷2 = 24(平方厘米)
(20 + 30 + 24)×2 = 148(平方厘米)
答:原来长方体的表面积是 148 平方厘米。
【点拨】首先根据长增加 2 厘米,宽和高不变, 体积就增加40立 方 厘米, 可得宽 ×高 = 40÷2 = 20(平方厘米);同理分别求出长×宽、长×高的值,然后把数据代入长方体的表面积计算公式解答即可。
几何与统计
一、填空。(每空 1 分,共 20 分)
1.在括号里填上合适的单位或数。
一个学生大约每天喝水 1.2( )。
一个花盆的体积大约是 5( )。
680 dm3 =( )m3
0.4 L =( )mL
34 dm3 =( )cm3
1.5 L =( )dm3 =( )cm3
2.钟面上时针从数字 2 顺时针旋转 90°到达数字( ),然后再从这个位置顺时针旋转 90°到达数字( )。
3.把 60 升水倒入一个长 6 分米、宽 2.5 分米的长方体水箱内,正好倒满,这个水箱的高是( )分米。
4.有一个长方体玻璃缸,长 1 米,宽 8 分米,高 6 分米,里面水深 4.5 分米。如果在缸中投入一块棱长是 5 分米的正方体铁块,那么水将溢出( )升。
5.有一个长方体纸盒,从里面量得长 36 厘米、宽 12 厘米、高 5 厘米。把棱长为 5 厘米的正方体装入长方体纸盒内且正方体不能露出,最多能装( )个这样的正方体。
6.如图是“俄罗斯方块”游戏的一个画面,要使左上角的图形经过平移插入到下面的空白处,应先向( )平移( )格,再向( )平移( )格。
7.如图是军军和亮亮五次电脑打字的字数统计图,根据统计图回答问题。
(1)第三次军军打的字数是亮亮打的字数的( )。
(2)他俩第( )次打字的字数相同,都是( )个。
(3)( )的打字速度一直在上升。
二、选择。(将正确答案的序号填在括号里)(每小题 2 分,共 14 分)
1.【新考法】将一个电话号码牌绕点 O 逆时针旋转 180°后如图所示,这个电话号码是( )。
A.9906089 B.6606089 C.6609089 D.6806099
2.下面的图案中,( )是由平移形成的。
3.同同想了解去年 12 月期间某市每天最高气温和最低气温的变化情况,她应该制作( )统计图。
A.单式条形 B.复式条形 C.单式折线 D.复式折线
4.下面的图形中,( )是轴对称图形。
5.一个大正方体的体积是小正方体的 8 倍,则这个大正方体的棱长之和是小正方体的棱长之和的( )倍。
A.2 B.4 C.6 D.8
6.【新题型】把10升水倒入一个长 2.5 分米、宽 20 厘米、高 5 分米的长方体水缸中。你能求出此时水面的高度吗?要解决这个问题,需要用到的信息有( )。
A.10 升、2.5 分米、20 厘米、5 分米
B.10 升、2.5 分米、20 厘米
C.2.5 分米、20 厘米、5 分米
D.10 升、20 厘米、5 分米
7.肖勇和妹妹一起去上学,途中肖勇发现忘带作业本了,于是他跑回家,拿上作业本, 马上向学校飞奔而去,刚好在学校门口追上了妹妹。下面四幅图中,( )描述的是肖勇和妹妹上学路上的情景。
三、动手操作。(共 22 分)
1.按要求画出下面的图形。
(1)画出图①绕点 O 逆时针旋转 90°后的图形。(4 分)
(2)画出图②的另一半,使它成为轴对称图形。(4 分)
2.纸质无人机因价格低廉、轻盈便携,颇受人们喜爱。下面是两架纸质无人机在一次调试飞行中的时间和高度记录统计表。
时间 第5秒 第10秒 第15秒 第20秒 第25秒 第30秒
甲无人机高度(米) 10 15 23 28 25 24
乙无人机高度(米) 12 20 23 23 20 5
(1)请根据统计表中的数据把下面的统计图补充完整。(4 分)
(2)从图上看,起飞后第( )秒两架无人机处于同一高度;起飞后第( )秒两架无人机的高度相差最大。(4 分)
(3)从起飞后第 15 秒至第 20 秒,甲无人机的飞行状态呈什么变化趋势?乙无人机的飞行状态呈什么变化趋势?(6 分)
四、解决问题。(共 44 分)
1.一件雕塑的底座是用混凝土浇筑成的长方体,它的高是 2.8 米,底面是边长为 2.5 米的正方形。这件雕塑的占地面积是多少平方米?浇筑这件雕塑的底座需要混凝土多少立方米?(8 分)
2.为了测出一块石头的体积,华华找来一个长 15 厘米、宽 10 厘米、足够高的长方体塑料盒子(如图),并倒入 10 厘米高的水,然后把石头浸没在水中,这时水面高 15 厘米。 这块石头的体积是多少立方厘米?(9 分)
3.挖一条长200米的水渠,水渠的横截面是一个梯形(如图)。一共要挖出多少立方米的土? (9 分)
4.【新情境】孔明灯,又叫天灯、许愿灯,是一种古老的手工艺品。在古代,孔明灯多用于军事方面;在现代,孔明灯多用来祈福。
(1)制作长方体孔明灯时,除了底面外,其他面都要糊上安全阻燃棉纸。制作一个如图所示的孔明灯,至少需要多少平方厘米的安全阻燃棉纸?(6 分)
(2)制作一个这样的孔明灯框架,至少需要多少厘米的竹条?(6 分)
(3)这个孔明灯的体积是多少立方厘米?(6 分)
★附加题:天才的你,试一试。(10 分)
一个长方体,如果长增加 2 厘米,宽和高不变,那么体积就增加 40 立方厘米;如果高增加 2 厘米,长和宽不变,那么体积就增加 60 立方厘米;如果宽增加 2 厘米,长和高不变,那么体积就增加 48 立方厘米。原来长方体的表面积是多少平方厘米?
答案
一、1.升 立方分米 0.68 400 34000
1.5 1500
2.5 8 3.4 4.5 5.14
6.右 1 下 3
7.(1)(2)四 45 (3)亮亮
二、1.C 2.A 3.D 4.B 5.A 6.B
7.A 【点拨】两人一开始一起去上学,所以速度一样,最后两人同时到校,所以 A 选项符合肖勇和妹妹上学路上的情景。
(2)15 30
(3)甲无人机一直上升,并在第 20 秒达到最大高度;乙无人机平稳飞行,高度没有发生变化。
四、1.2.5×2.5 = 6.25(平方米) 6.25×2.8 = 17.5(立方米)
答:这件雕塑的占地面积是 6.25 平方米。浇筑这件雕塑的底座需要混凝土 17.5 立方米。
2.15 - 10 = 5(厘米) 15×10×5 = 750(立方厘米)
答:这块石头的体积是 750 立方厘米。
3.(2 + 4)×2÷2×200 = 1200(立方米)
答:一共要挖出 1200 立方米的土。
4.(1)30×50×4 + 30×30 = 6900(平方厘米)
答:至少需要 6900 平方厘米的安全阻燃棉纸。
(2)(30 + 30 + 50)×4 = 440(厘米)
答:至少需要 440 厘米的竹条。
(3)30×30×50 = 45000(立方厘米)
答:这个孔明灯的体积是 45000 立方厘米。
附加题:宽 × 高 = 40÷2 = 20(平方厘米)
长 × 宽 = 60÷2 = 30(平方厘米)
长 × 高 = 48÷2 = 24(平方厘米)
(20 + 30 + 24)×2 = 148(平方厘米)
答:原来长方体的表面积是 148 平方厘米。
【点拨】首先根据长增加 2 厘米,宽和高不变, 体积就增加40立 方 厘米, 可得宽 ×高 = 40÷2 = 20(平方厘米);同理分别求出长×宽、长×高的值,然后把数据代入长方体的表面积计算公式解答即可。
同课章节目录
