人教版九年级上册第二十二章课件(共19张PPT) 二次函数与一元二次方程说课
文档属性
| 名称 | 人教版九年级上册第二十二章课件(共19张PPT) 二次函数与一元二次方程说课 |  | |
| 格式 | pptx | ||
| 文件大小 | 940.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-31 09:53:42 | ||
图片预览






文档简介
(共19张PPT)
二次函数与一元二次方程
(第一课时)
1、知识的获得是一个主动过程,数学教育要以有利于学生的全面发展为中心,以提供有价值的数学和倡导有意义的学习方式为基本点。
2、本节课的设计努力体现学生的主体地位,力求使学生经历“课前预习—自主学习----小组讨论—--成果展示—例题讲解—课后应用”的过程,提高学生的解题能力,培养学生运用数学的意识和能力。
一、设计理念
二、教材分析
承上:1、 用函数解决问题的进一步探讨。
2、一次函数与一元一次方程关系的延续。
3、把函数与研究方程的根联系起来。
启下:
1、为高中数学求一元二次不等式的解集奠定基础。
2、函数与方程在问题解决中互相转化是学生在今后必不可少的一个能力。
已形成的:
1、能理解二次函数的性质、图象,有一定看图识图能力,并能画一次函数、二次函数的草图。
2、能熟练求解一元二次方程的根 。
有待形成、提升的:
1、理解二次函数与一元二次方程的联系和研究时互相转化的数学思想及数形结合思想。
2、用函数的观点解决问题的应用意识。
三、学情分析
【教学重点】
1.掌握方程与函数之间的联系.
2. 掌握一元二次方程的实数根个数与二次函数与x轴公共点个数的对应关系,根据具体的函数图像解决有关问题;
3.掌握一元二次方程的根就是二次函数与y =m交点的横坐标.
【教学难点】
1、掌握二次函数与x 轴交点的个数与一元二次方程的根的个数之间的关系. 探索方程与函数之间的联系的过程.
2、熟练掌握由方程根来求求待定系数,或由待定系数的取值决定方程根的解题套路.
四、重点难点分析
2、学法分析
1、教法分析
学生对二次函数与一元二次方程之间的关系已经很清楚,主要是将知识能力转化为解题能力。采用“讲练法”的方式,引导学生经历“回顾旧知—课前练习----知识总结—例题讲解---方法归纳—课后应用”的过程,使学生掌握熟练解决有关问题。
教师引导启发 学生合作探索
五、教法、学法分析
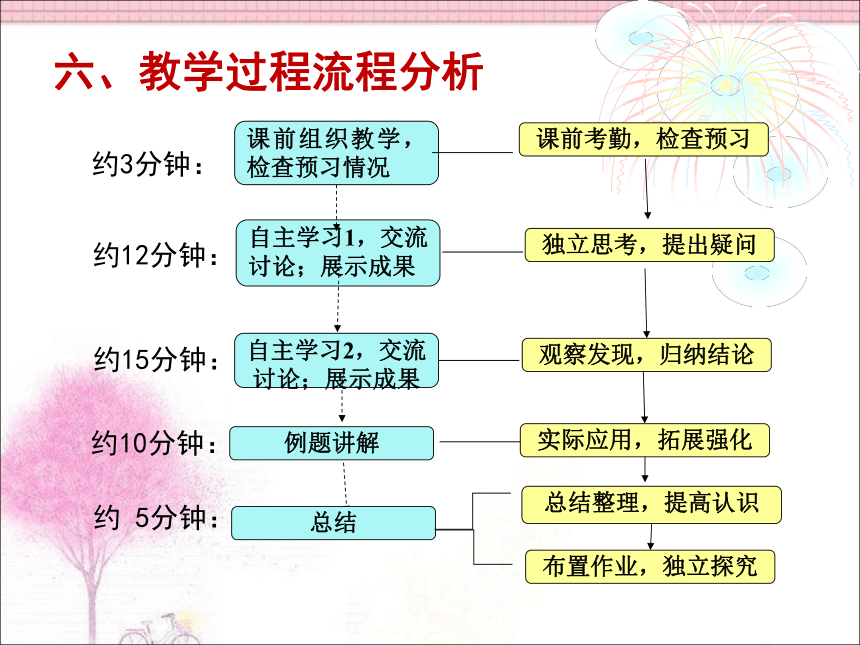
课前组织教学,检查预习情况
自主学习1,交流讨论;展示成果
课前考勤,检查预习
独立思考,提出疑问
观察发现,归纳结论
自主学习2,交流讨论;展示成果
实际应用,拓展强化
约3分钟:
约12分钟:
约15分钟:
约10分钟:
总结
例题讲解
约 5分钟:
总结整理,提高认识
布置作业,独立探究
六、教学过程流程分析
检查预习情况:
1.掌握抛物线y=ax2+bx+c和x轴的交点个数与
b2-4ac的符号之间的关系
(1)当b2-4ac>0时,抛物线与x轴有 个交点.
(2)当b2-4ac=0时,抛物线与x轴有 个交点.
(3)当b2-4ac<0时,抛物线与x轴 交点.
2.理解y=ax2+bx+c与ax2+bx+c=0的关系
如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标是x0,那么当x=x0时,函数值是 ,即x= 是方程ax2+bx+c=0的一个根.
两
一
没有
0
x0
问题 如图,以40m/s的速度将小球沿与地面成300角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行h(单位:m)与飞行时间t(单位:s)之间具有关系:h=20t-5t2,考虑以下问题:
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
自学学习1:
自学课本P43页-44页思考以上内容
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
你能结合图形指出:
为什么在两个时间
球的高度为15m?
O
h
t
15
1
3
讨论展示
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
你能结合图形指出:
为什么只在一个时间球的高度为20m?
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
O
h
t
你能结合图形指出:
为什么球不能达到20.5m的高度
20.5
讨论展示:
(4)球从飞出到落地要用多少时间?
你能结合图形指出:
为什么在两个时间球的高度为0m吗
例如,已知二次函数y=-X2+4x的值为3,求自变量x的值.
就是求方程3=-X2+4x的解,
例如,解方程X2-4x+3=0
就是已知二次函数y=X2-4x+3的值为0,求自变量x的值.
归纳小结:
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系
自主学习2
自学课本P44页思考至45页内容,思考下列问题:
判别式: b2-4ac 二次函数 y=ax2+bx+c (a≠0) 图象 一元二次方程ax2+bx+c=0
(a≠0)的根
x
y
O
与x轴有两个不同的交点
(x1,0)
(x2,0)
有两个不同的解
x=x1,x=x2
b2-4ac>0
x
y
O
与x轴有唯一个
交点
有两个相等的解
x1=x2=
b2-4ac=0
x
y
O
与x轴没有
交点
没有实数根
b2-4ac<0
讨论归纳:
课本47页 1、2、5
反思检测:
课外拓展:
已知二次函数y=x2+2x+m的图象与x轴有且只有一个公共点.
(1)求m的值;
(2)若P(n,y1),Q(2,y2)是二次函数y=x2+2x+m上的两点,且y1>y2,利用函数图像直接写出实数n的取值范围.
设计意图:本题考查了抛物线和x轴的交点问题,二次函数的性质以及二次函数图象上点的坐标特点。利用图像解决问题是关键。
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
(1)有两个交点
(2)有一个交点
(3)没有交点
b2 – 4ac > 0
b2 – 4ac= 0
b2 – 4ac< 0
若抛物线y=ax2+bx+c与x轴有交点,则
b2 – 4ac
≥0
课堂小结
1、必做题:
课本47页第 4、6题
课后作业:
1.已知二次函数y=-x +2x+k+2与x轴的公共点有两个,
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;观察图象,当x取何值时,y=0,y>0,y<0
2.已知:函数y=ax +(3a-1)x+2a+1 (a为常数).
若该函数图象是开口向上的抛物线,与x轴相交于点A(x1,0),B(x2,0)两点,
AB=2.求抛物线的解析式
2、选作题:
设计意图:
让学生既能体会到学数学的成功感,又能恰当的提高学生的兴趣,并与中考题型接轨。
二次函数与一元二次方程
(第一课时)
1、知识的获得是一个主动过程,数学教育要以有利于学生的全面发展为中心,以提供有价值的数学和倡导有意义的学习方式为基本点。
2、本节课的设计努力体现学生的主体地位,力求使学生经历“课前预习—自主学习----小组讨论—--成果展示—例题讲解—课后应用”的过程,提高学生的解题能力,培养学生运用数学的意识和能力。
一、设计理念
二、教材分析
承上:1、 用函数解决问题的进一步探讨。
2、一次函数与一元一次方程关系的延续。
3、把函数与研究方程的根联系起来。
启下:
1、为高中数学求一元二次不等式的解集奠定基础。
2、函数与方程在问题解决中互相转化是学生在今后必不可少的一个能力。
已形成的:
1、能理解二次函数的性质、图象,有一定看图识图能力,并能画一次函数、二次函数的草图。
2、能熟练求解一元二次方程的根 。
有待形成、提升的:
1、理解二次函数与一元二次方程的联系和研究时互相转化的数学思想及数形结合思想。
2、用函数的观点解决问题的应用意识。
三、学情分析
【教学重点】
1.掌握方程与函数之间的联系.
2. 掌握一元二次方程的实数根个数与二次函数与x轴公共点个数的对应关系,根据具体的函数图像解决有关问题;
3.掌握一元二次方程的根就是二次函数与y =m交点的横坐标.
【教学难点】
1、掌握二次函数与x 轴交点的个数与一元二次方程的根的个数之间的关系. 探索方程与函数之间的联系的过程.
2、熟练掌握由方程根来求求待定系数,或由待定系数的取值决定方程根的解题套路.
四、重点难点分析
2、学法分析
1、教法分析
学生对二次函数与一元二次方程之间的关系已经很清楚,主要是将知识能力转化为解题能力。采用“讲练法”的方式,引导学生经历“回顾旧知—课前练习----知识总结—例题讲解---方法归纳—课后应用”的过程,使学生掌握熟练解决有关问题。
教师引导启发 学生合作探索
五、教法、学法分析
课前组织教学,检查预习情况
自主学习1,交流讨论;展示成果
课前考勤,检查预习
独立思考,提出疑问
观察发现,归纳结论
自主学习2,交流讨论;展示成果
实际应用,拓展强化
约3分钟:
约12分钟:
约15分钟:
约10分钟:
总结
例题讲解
约 5分钟:
总结整理,提高认识
布置作业,独立探究
六、教学过程流程分析
检查预习情况:
1.掌握抛物线y=ax2+bx+c和x轴的交点个数与
b2-4ac的符号之间的关系
(1)当b2-4ac>0时,抛物线与x轴有 个交点.
(2)当b2-4ac=0时,抛物线与x轴有 个交点.
(3)当b2-4ac<0时,抛物线与x轴 交点.
2.理解y=ax2+bx+c与ax2+bx+c=0的关系
如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标是x0,那么当x=x0时,函数值是 ,即x= 是方程ax2+bx+c=0的一个根.
两
一
没有
0
x0
问题 如图,以40m/s的速度将小球沿与地面成300角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行h(单位:m)与飞行时间t(单位:s)之间具有关系:h=20t-5t2,考虑以下问题:
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
自学学习1:
自学课本P43页-44页思考以上内容
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
你能结合图形指出:
为什么在两个时间
球的高度为15m?
O
h
t
15
1
3
讨论展示
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
你能结合图形指出:
为什么只在一个时间球的高度为20m?
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
O
h
t
你能结合图形指出:
为什么球不能达到20.5m的高度
20.5
讨论展示:
(4)球从飞出到落地要用多少时间?
你能结合图形指出:
为什么在两个时间球的高度为0m吗
例如,已知二次函数y=-X2+4x的值为3,求自变量x的值.
就是求方程3=-X2+4x的解,
例如,解方程X2-4x+3=0
就是已知二次函数y=X2-4x+3的值为0,求自变量x的值.
归纳小结:
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系
自主学习2
自学课本P44页思考至45页内容,思考下列问题:
判别式: b2-4ac 二次函数 y=ax2+bx+c (a≠0) 图象 一元二次方程ax2+bx+c=0
(a≠0)的根
x
y
O
与x轴有两个不同的交点
(x1,0)
(x2,0)
有两个不同的解
x=x1,x=x2
b2-4ac>0
x
y
O
与x轴有唯一个
交点
有两个相等的解
x1=x2=
b2-4ac=0
x
y
O
与x轴没有
交点
没有实数根
b2-4ac<0
讨论归纳:
课本47页 1、2、5
反思检测:
课外拓展:
已知二次函数y=x2+2x+m的图象与x轴有且只有一个公共点.
(1)求m的值;
(2)若P(n,y1),Q(2,y2)是二次函数y=x2+2x+m上的两点,且y1>y2,利用函数图像直接写出实数n的取值范围.
设计意图:本题考查了抛物线和x轴的交点问题,二次函数的性质以及二次函数图象上点的坐标特点。利用图像解决问题是关键。
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
(1)有两个交点
(2)有一个交点
(3)没有交点
b2 – 4ac > 0
b2 – 4ac= 0
b2 – 4ac< 0
若抛物线y=ax2+bx+c与x轴有交点,则
b2 – 4ac
≥0
课堂小结
1、必做题:
课本47页第 4、6题
课后作业:
1.已知二次函数y=-x +2x+k+2与x轴的公共点有两个,
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;观察图象,当x取何值时,y=0,y>0,y<0
2.已知:函数y=ax +(3a-1)x+2a+1 (a为常数).
若该函数图象是开口向上的抛物线,与x轴相交于点A(x1,0),B(x2,0)两点,
AB=2.求抛物线的解析式
2、选作题:
设计意图:
让学生既能体会到学数学的成功感,又能恰当的提高学生的兴趣,并与中考题型接轨。
同课章节目录
