16.2 二次根式的乘除 第2课时 课件(共19张PPT) 人教版数学八年级下册
文档属性
| 名称 | 16.2 二次根式的乘除 第2课时 课件(共19张PPT) 人教版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 17:43:18 | ||
图片预览



文档简介
(共19张PPT)
16.2 二次根式的乘除
配套人教版
第2课时
4.经历探究、归纳和应用等数学活动,培养由特殊到一般的
归纳探究精神,提升逆向思维能力.
3.利用商的算术平方根的性质或分母有理化化简二次根式;
2.会进行二次根式的除法运算;
1.理解并掌握二次根式的除法法则和商的算术平方根的性质;
学习目标
二次根式
的乘除
(2)
难点
重点
难点
巩固新知
课堂小结
布置作业
应用新知
创设情境
探究新知
复习引入
1.二次根式的乘法法则是怎样的?
2.逆用二次根式的乘法法则可以得到什么?
一般地,二次根式的乘法法则是:
算术平方根的积等于被开方数的积的算术平方根.
反过来,可得积的算术平方根的性质:
积的算术平方根等于积中各因式的算术平方根的积.
这节课我们一起来研究这个问题.
二次根式的除法
法则是怎样的呢?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
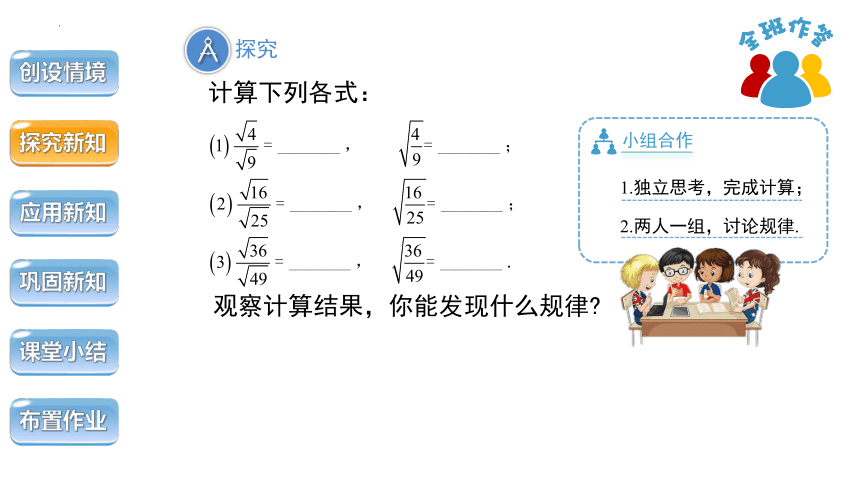
探究
小组合作
1.独立思考,完成计算;
2.两人一组,讨论规律.
计算下列各式:
观察计算结果,你能发现什么规律
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
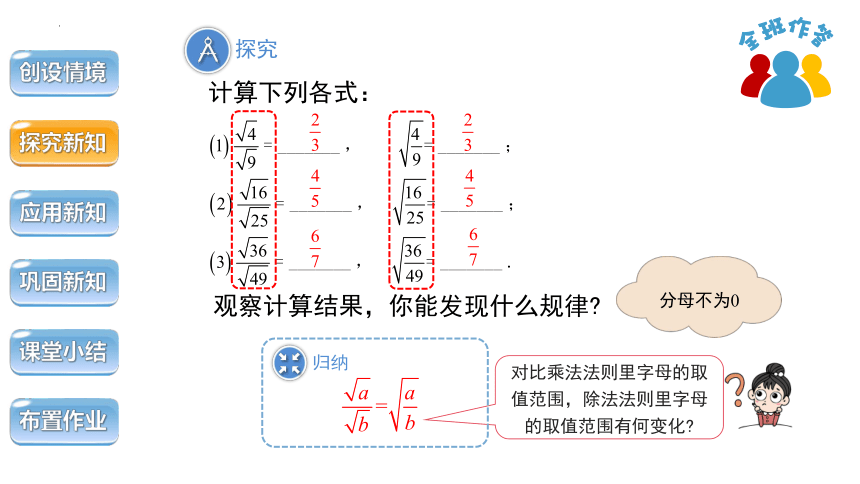
探究
计算下列各式:
对比乘法法则里字母的取值范围,除法法则里字母的取值范围有何变化
观察计算结果,你能发现什么规律
分母不为0
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
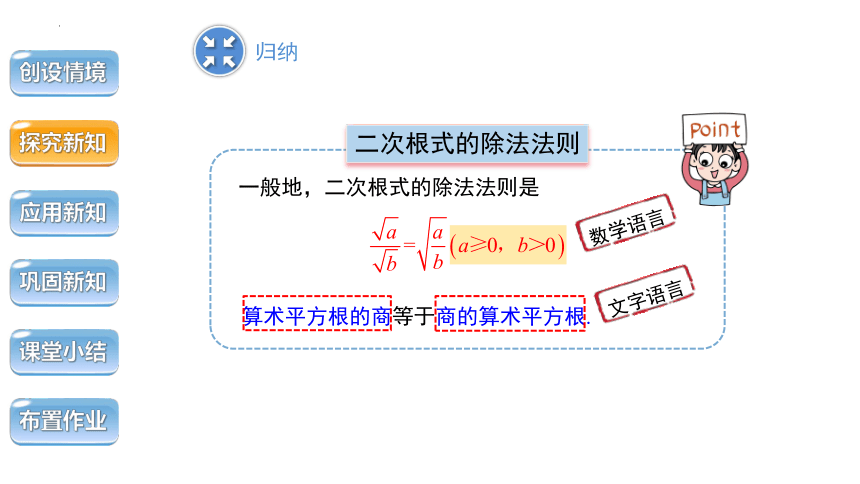
二次根式的除法法则
一般地,二次根式的除法法则是
算术平方根的商等于商的算术平方根.
数学语言
文字语言
归纳
巩固新知
课堂小结
布置作业
创设情境
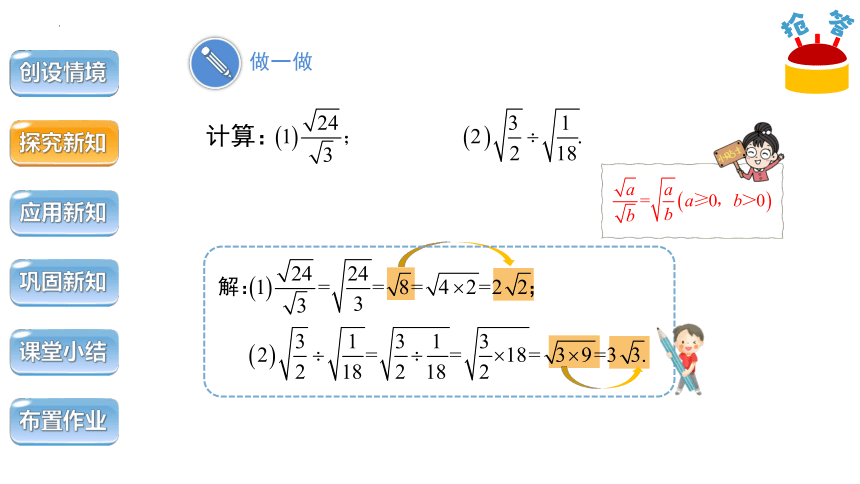
计算:
做一做
创设情境
探究新知
应用新知
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
商的算术平方根的性质
商的算术平方根等于算术平方根的商.
类比探究
利用商的算术平方根的性质可以进行二次根式的化简.
数学语言
文字语言
把 反过来,可得:
巩固新知
课堂小结
布置作业
创设情境
化简:
做一做
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
①被开方数不含分母;
②被开方数中不含能开得尽方的因数(或因式).
最简二次根式的概念
应用新知
探究新知
你能从上面的解答过程中,总结一下二次根式的运算结果有什么特征吗?
探究
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
典型例题
在解法2中,式子变形
是为了去掉分母中的根号.
【例1】计算:
当分母中含有被开方数时,我们可以利用分式的基本性质,分子、分母同乘一个适当的因式,化去分母中的根号,即进行分母有理化.
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
【例1】计算:
典型例题
在二次根式的运算中,一般
要把最后结果化成最简二次根式,并且分母中不含二次根式.
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
【例2】设长方形的面积为S,相邻两边长分别为a,b.
已知 ,求a.
典型例题
结果要写成
最简二次根式.
1.辨别下列二次根式是否是最简二次根式.
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
最简二次根式的概念:
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式.
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
2.把下列二次根式化成最简二次根式:
课堂小结
布置作业
探究新知
创设情境
3.计算:
随堂练习
应用新知
巩固新知
二次根式
的乘除
(2)
一般地,二次根式的除法法则是
算术平方根的商等于商的算术平方根.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
除法法则
商的算术平方根的性质
反过来,可得商的算术平方根的性质
商的算术平方根等于算术平方根的商.
最简二次根式
1.被开方数不含分母;
2.被开方数中不含能开得尽方的因数或因式.
布置作业
课本第10-11页
习题16.2:2,6.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
16.2 二次根式的乘除
配套人教版
第2课时
4.经历探究、归纳和应用等数学活动,培养由特殊到一般的
归纳探究精神,提升逆向思维能力.
3.利用商的算术平方根的性质或分母有理化化简二次根式;
2.会进行二次根式的除法运算;
1.理解并掌握二次根式的除法法则和商的算术平方根的性质;
学习目标
二次根式
的乘除
(2)
难点
重点
难点
巩固新知
课堂小结
布置作业
应用新知
创设情境
探究新知
复习引入
1.二次根式的乘法法则是怎样的?
2.逆用二次根式的乘法法则可以得到什么?
一般地,二次根式的乘法法则是:
算术平方根的积等于被开方数的积的算术平方根.
反过来,可得积的算术平方根的性质:
积的算术平方根等于积中各因式的算术平方根的积.
这节课我们一起来研究这个问题.
二次根式的除法
法则是怎样的呢?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
小组合作
1.独立思考,完成计算;
2.两人一组,讨论规律.
计算下列各式:
观察计算结果,你能发现什么规律
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
计算下列各式:
对比乘法法则里字母的取值范围,除法法则里字母的取值范围有何变化
观察计算结果,你能发现什么规律
分母不为0
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
二次根式的除法法则
一般地,二次根式的除法法则是
算术平方根的商等于商的算术平方根.
数学语言
文字语言
归纳
巩固新知
课堂小结
布置作业
创设情境
计算:
做一做
创设情境
探究新知
应用新知
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
商的算术平方根的性质
商的算术平方根等于算术平方根的商.
类比探究
利用商的算术平方根的性质可以进行二次根式的化简.
数学语言
文字语言
把 反过来,可得:
巩固新知
课堂小结
布置作业
创设情境
化简:
做一做
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
①被开方数不含分母;
②被开方数中不含能开得尽方的因数(或因式).
最简二次根式的概念
应用新知
探究新知
你能从上面的解答过程中,总结一下二次根式的运算结果有什么特征吗?
探究
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
典型例题
在解法2中,式子变形
是为了去掉分母中的根号.
【例1】计算:
当分母中含有被开方数时,我们可以利用分式的基本性质,分子、分母同乘一个适当的因式,化去分母中的根号,即进行分母有理化.
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
【例1】计算:
典型例题
在二次根式的运算中,一般
要把最后结果化成最简二次根式,并且分母中不含二次根式.
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
【例2】设长方形的面积为S,相邻两边长分别为a,b.
已知 ,求a.
典型例题
结果要写成
最简二次根式.
1.辨别下列二次根式是否是最简二次根式.
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
最简二次根式的概念:
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式.
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
2.把下列二次根式化成最简二次根式:
课堂小结
布置作业
探究新知
创设情境
3.计算:
随堂练习
应用新知
巩固新知
二次根式
的乘除
(2)
一般地,二次根式的除法法则是
算术平方根的商等于商的算术平方根.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
除法法则
商的算术平方根的性质
反过来,可得商的算术平方根的性质
商的算术平方根等于算术平方根的商.
最简二次根式
1.被开方数不含分母;
2.被开方数中不含能开得尽方的因数或因式.
布置作业
课本第10-11页
习题16.2:2,6.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
