2.5直线与圆的位置关系(2)课件(共17张PPT) 苏科版数学九年级上册
文档属性
| 名称 | 2.5直线与圆的位置关系(2)课件(共17张PPT) 苏科版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 230.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 17:53:30 | ||
图片预览


文档简介
(共17张PPT)
2.5直线与圆的位置关系(2)
【学习目标】
1、掌握圆的切线的性质定理;
2、能利用圆的性质去解决相关问题.
A
O
l
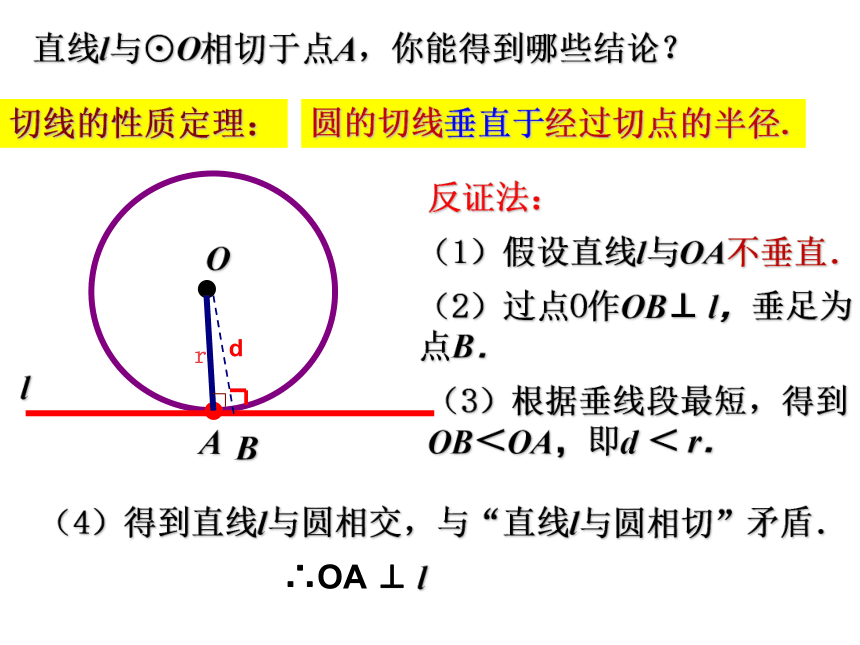
直线l与⊙O相切于点A,你能得到哪些结论?
圆的切线垂直于经过切点的半径.
切线的性质定理:
反证法:
(1)假设直线l与OA不垂直.
(2)过点O作OB⊥ l,垂足为点B.
(4)得到直线l与圆相交,与“直线l与圆相切”矛盾.
(3)根据垂线段最短,得到OB<OA,即d < r.
B
∟
r
∴OA ⊥ l
d
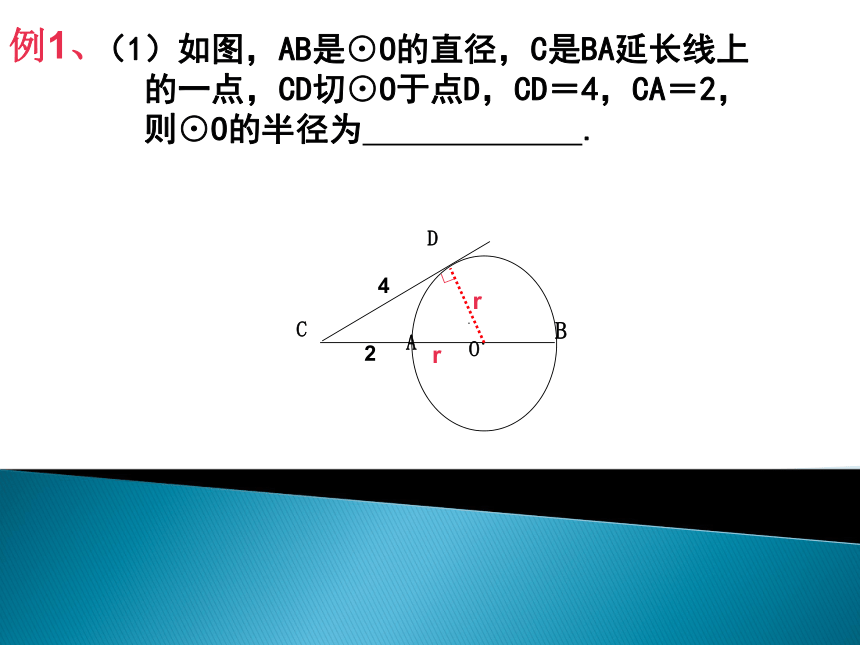
(1)如图,AB是⊙O的直径,C是BA延长线上
的一点,CD切⊙O于点D,CD=4,CA=2,
则⊙O的半径为 .
例1、
D
A
B
C
O
·
﹒
4
2
∟
r
r
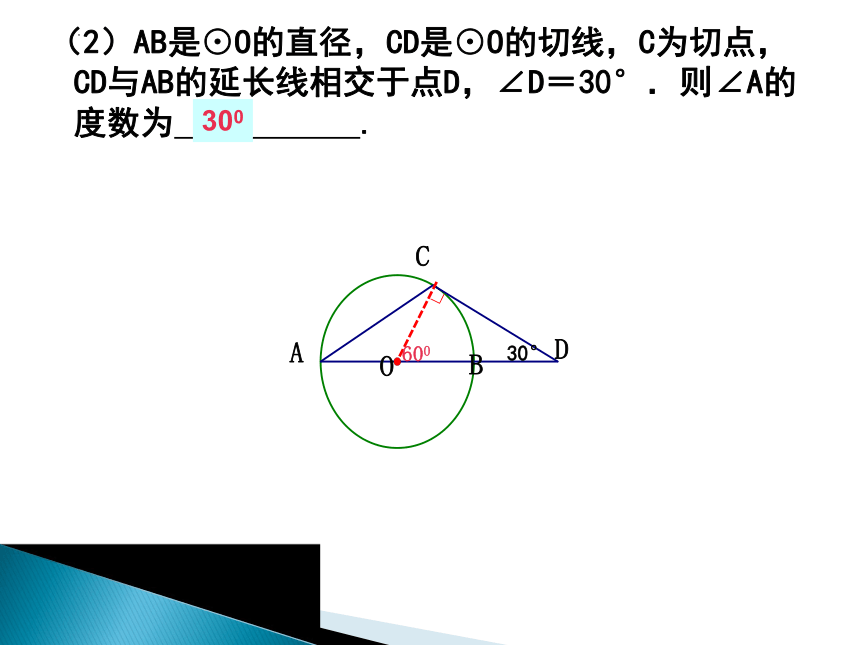
(2)AB是⊙O的直径,CD是⊙O的切线,C为切点,CD与AB的延长线相交于点D,∠D=30°.则∠A的度数为 .
A
O
B
D
C
30°
∟
600
300
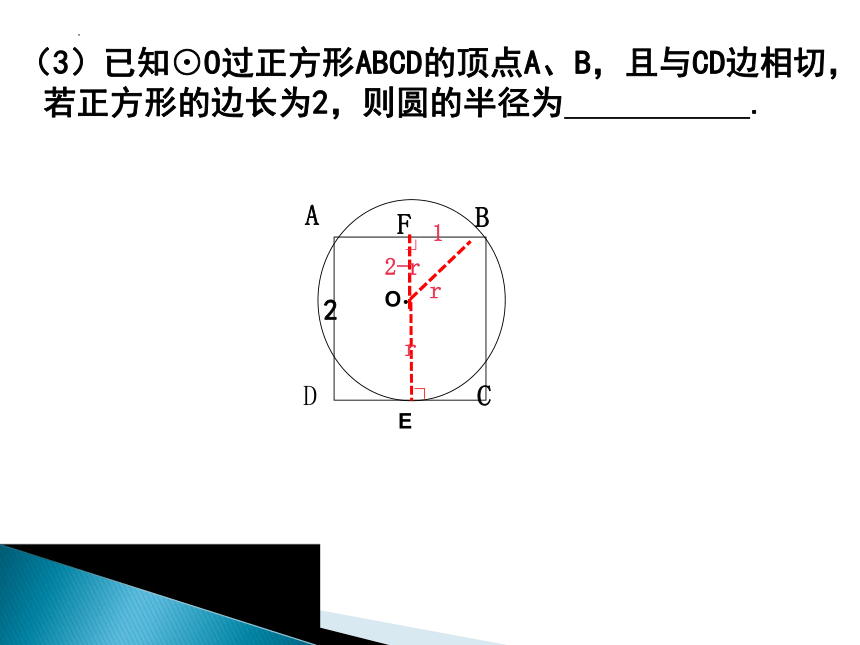
(3)已知⊙O过正方形ABCD的顶点A、B,且与CD边相切,若正方形的边长为2,则圆的半径为 .
A
B
D
C
﹒
O
E
∟
2
∟
F
r
r
2-r
1
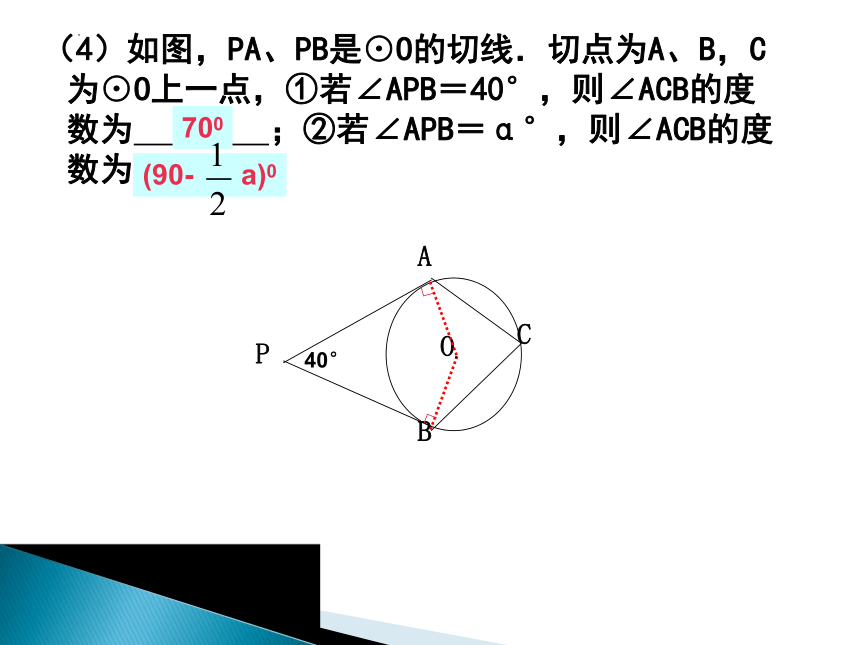
(4)如图,PA、PB是⊙O的切线.切点为A、B,C为⊙O上一点,①若∠APB=40°,则∠ACB的度数为 ;②若∠APB=α°,则∠ACB的度数为 .
A
P
B
C
O
∟
∟
40°
﹒
700
(90- a)0
例2、如图,在同心圆O中,大圆的弦AB切小圆点P,(1)试说明:PA=PB;(2)若AB=6,求圆环的面积.
B
O
A
P
∟
r
R
例3 如图,AB是⊙O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,DE与AC有怎样的位置关系?为什么?
1
2
∟
3
∟
例4、OC是∠AOB的角平分线,点M是OC上一点,⊙M 与OB相切,则直线OA与⊙M是怎样的位置关系?
A
C
B
M
O
1
2
∟
∟
r
D
E
d
1、如图,直线AC切半径为3cm的⊙O于点B,AB= cm,BC=3cm,则∠AOC的度数是 .
O
C
B
A
3
∟
3
1050
课堂练习
2、已知:如图,直线BC切⊙O于点C,PD是⊙O的直径,∠A=28°,∠B=26°,则∠PDC= °.
A
C
O
P
B
D
∟
28°
26°
36
3、以三角形的一边为直径的圆恰好与另一边相切,则此三角形是 .
4、等腰△ABC的腰AB=AC=4cm,若以A为圆心,2cm为半径的圆与BC相切,则∠BAC的度数为( )
A、30° B、60° C、90° D、120°
直角三角形
D
5、如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点D.图中互余的角有( )
A、1对 B、2对
C、3对 D、4对
B
C
D
A
O
D
∟
∟
1
2
3
4
6、如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,
AB=4,OM=1,则PA的长为 ( )
A、 B、 C、 D、
P
A
O
M
B
4
1
∟
∟
2
C
7、如图,AB是⊙O的直径,MN切⊙O于点C,且∠BCM=38°,求∠ABC的度数.
O
A
B
C
M
N
∟
38°
8、如图,PA、PB是⊙O的切线,切点分别为点A、B,AC是⊙O的直径,∠ACB=70°,求∠P的度数.
O
A
B
C
P
70°
∟
∟
1400
400
2.5直线与圆的位置关系(2)
【学习目标】
1、掌握圆的切线的性质定理;
2、能利用圆的性质去解决相关问题.
A
O
l
直线l与⊙O相切于点A,你能得到哪些结论?
圆的切线垂直于经过切点的半径.
切线的性质定理:
反证法:
(1)假设直线l与OA不垂直.
(2)过点O作OB⊥ l,垂足为点B.
(4)得到直线l与圆相交,与“直线l与圆相切”矛盾.
(3)根据垂线段最短,得到OB<OA,即d < r.
B
∟
r
∴OA ⊥ l
d
(1)如图,AB是⊙O的直径,C是BA延长线上
的一点,CD切⊙O于点D,CD=4,CA=2,
则⊙O的半径为 .
例1、
D
A
B
C
O
·
﹒
4
2
∟
r
r
(2)AB是⊙O的直径,CD是⊙O的切线,C为切点,CD与AB的延长线相交于点D,∠D=30°.则∠A的度数为 .
A
O
B
D
C
30°
∟
600
300
(3)已知⊙O过正方形ABCD的顶点A、B,且与CD边相切,若正方形的边长为2,则圆的半径为 .
A
B
D
C
﹒
O
E
∟
2
∟
F
r
r
2-r
1
(4)如图,PA、PB是⊙O的切线.切点为A、B,C为⊙O上一点,①若∠APB=40°,则∠ACB的度数为 ;②若∠APB=α°,则∠ACB的度数为 .
A
P
B
C
O
∟
∟
40°
﹒
700
(90- a)0
例2、如图,在同心圆O中,大圆的弦AB切小圆点P,(1)试说明:PA=PB;(2)若AB=6,求圆环的面积.
B
O
A
P
∟
r
R
例3 如图,AB是⊙O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,DE与AC有怎样的位置关系?为什么?
1
2
∟
3
∟
例4、OC是∠AOB的角平分线,点M是OC上一点,⊙M 与OB相切,则直线OA与⊙M是怎样的位置关系?
A
C
B
M
O
1
2
∟
∟
r
D
E
d
1、如图,直线AC切半径为3cm的⊙O于点B,AB= cm,BC=3cm,则∠AOC的度数是 .
O
C
B
A
3
∟
3
1050
课堂练习
2、已知:如图,直线BC切⊙O于点C,PD是⊙O的直径,∠A=28°,∠B=26°,则∠PDC= °.
A
C
O
P
B
D
∟
28°
26°
36
3、以三角形的一边为直径的圆恰好与另一边相切,则此三角形是 .
4、等腰△ABC的腰AB=AC=4cm,若以A为圆心,2cm为半径的圆与BC相切,则∠BAC的度数为( )
A、30° B、60° C、90° D、120°
直角三角形
D
5、如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点D.图中互余的角有( )
A、1对 B、2对
C、3对 D、4对
B
C
D
A
O
D
∟
∟
1
2
3
4
6、如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,
AB=4,OM=1,则PA的长为 ( )
A、 B、 C、 D、
P
A
O
M
B
4
1
∟
∟
2
C
7、如图,AB是⊙O的直径,MN切⊙O于点C,且∠BCM=38°,求∠ABC的度数.
O
A
B
C
M
N
∟
38°
8、如图,PA、PB是⊙O的切线,切点分别为点A、B,AC是⊙O的直径,∠ACB=70°,求∠P的度数.
O
A
B
C
P
70°
∟
∟
1400
400
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
