第六章 一次函数 复习课件 (共21张PPT) 苏科版数学八年级上册
文档属性
| 名称 | 第六章 一次函数 复习课件 (共21张PPT) 苏科版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 25.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 18:04:35 | ||
图片预览







文档简介
(共21张PPT)
第六章
一次函数 复习
学习目标:
1 、掌握函数及其相关概念,理解一次函数的定义、图像、性质以及它与正比例函数之间的关系;
2、能够利用一次函数模型解决生活中的实际问题,感受相关的数学思想方法。
3、能应用本章的基础知识熟练地解决数 学问题。
一次函数知识回顾:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。所以说正比例函数是一种特殊的一次函数
kx +b
≠0
=0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次;⑵比例系数 _____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点 (_____), 的_________。
一次函数y=kx+b(k≠0)的图象是过点(0, , 0)
的__________。
0,0
(1,k)
一条直线
b ),(
一条直线
3、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
一、三
增大
二、四
减小
4、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:
增大
减小
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
5.平移
(1)函数y=kx向上或向下平移|b ︱个单位长度得函数y=kx+b.
(2)函数y=kx向左或向右平移|m ︱个单位长度得函数y=k(x+m) =kx+km.
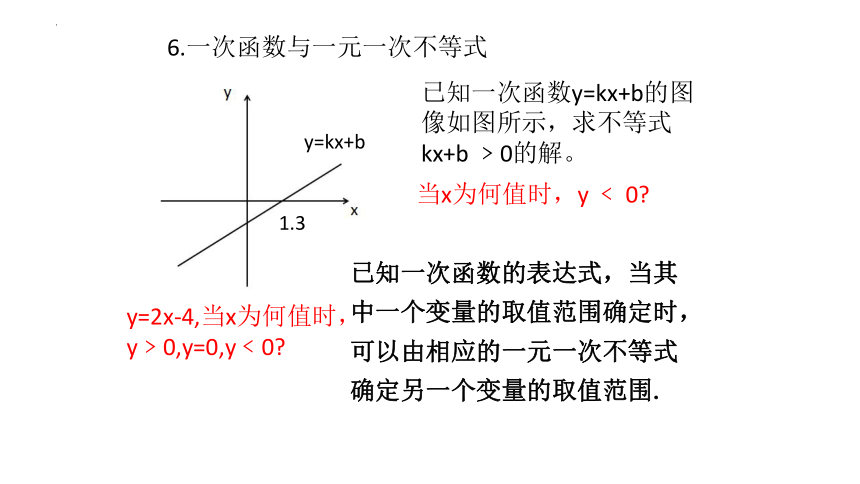
6.一次函数与一元一次不等式
y=kx+b
1.3
已知一次函数y=kx+b的图像如图所示,求不等式kx+b ﹥0的解。
当x为何值时,y ﹤ 0
已知一次函数的表达式,当其中一个变量的取值范围确定时,可以由相应的一元一次不等式确定另一个变量的取值范围.
y=2x-4,当x为何值时,
y﹥0,y=0,y﹤0
选一选
选一选:
C
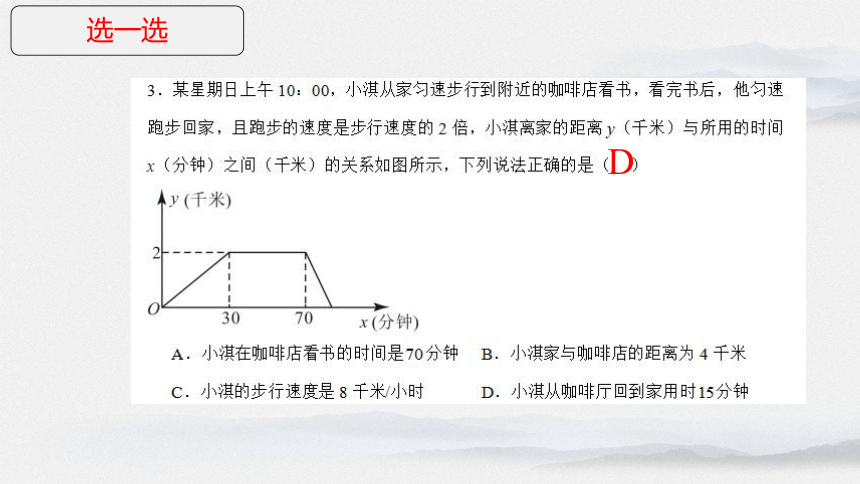
D
D
选一选
B
C
B
选一选
填一填:
-2
-2
y=2x-2
(3,0)
填一填:
填一填:
-2填一填:
填一填:
练一练:
拓展延伸:
课课堂检测
课课堂检测
6.小聪上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中。小聪离家的路程s(km)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)小聪去超市途中的速度是多少?回家途中的速度是多少?
0
(2)小聪在超市逗留了多少时间?
(3)用恰当的方式表示路程s与时间t之间的关系。
(4)小聪在来去途中,离家1km处的时间是几时几分?
本节课我们主要学习了函数图像在一次函数中的应用通过本节课的学习你有什么收获?
小结回顾
解决给出函数图像的问题时充分利用图像所反映的信息,尤其注意函数图像中关键点所反映的信息!注意数形结合思想的应用。
祝学有所获
第六章
一次函数 复习
学习目标:
1 、掌握函数及其相关概念,理解一次函数的定义、图像、性质以及它与正比例函数之间的关系;
2、能够利用一次函数模型解决生活中的实际问题,感受相关的数学思想方法。
3、能应用本章的基础知识熟练地解决数 学问题。
一次函数知识回顾:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。所以说正比例函数是一种特殊的一次函数
kx +b
≠0
=0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次;⑵比例系数 _____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点 (_____), 的_________。
一次函数y=kx+b(k≠0)的图象是过点(0, , 0)
的__________。
0,0
(1,k)
一条直线
b ),(
一条直线
3、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
一、三
增大
二、四
减小
4、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:
增大
减小
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
5.平移
(1)函数y=kx向上或向下平移|b ︱个单位长度得函数y=kx+b.
(2)函数y=kx向左或向右平移|m ︱个单位长度得函数y=k(x+m) =kx+km.
6.一次函数与一元一次不等式
y=kx+b
1.3
已知一次函数y=kx+b的图像如图所示,求不等式kx+b ﹥0的解。
当x为何值时,y ﹤ 0
已知一次函数的表达式,当其中一个变量的取值范围确定时,可以由相应的一元一次不等式确定另一个变量的取值范围.
y=2x-4,当x为何值时,
y﹥0,y=0,y﹤0
选一选
选一选:
C
D
D
选一选
B
C
B
选一选
填一填:
-2
-2
y=2x-2
(3,0)
填一填:
填一填:
-2
填一填:
练一练:
拓展延伸:
课课堂检测
课课堂检测
6.小聪上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中。小聪离家的路程s(km)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)小聪去超市途中的速度是多少?回家途中的速度是多少?
0
(2)小聪在超市逗留了多少时间?
(3)用恰当的方式表示路程s与时间t之间的关系。
(4)小聪在来去途中,离家1km处的时间是几时几分?
本节课我们主要学习了函数图像在一次函数中的应用通过本节课的学习你有什么收获?
小结回顾
解决给出函数图像的问题时充分利用图像所反映的信息,尤其注意函数图像中关键点所反映的信息!注意数形结合思想的应用。
祝学有所获
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
