浙教版九年级上册期末提升数学卷(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版九上期末提升卷(含解析)
一、单选题
1.已知二次函数,当时,y的最小值为( )
A. B. C. D.7
2.如图,在△ABC中,∠CAB=66°.在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'的度数为( )
A.70° B.50° C.40° D.48°
3.一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6个点)抛掷n次,若n次抛掷所出现的向上一面的点数之和大于n2,则算过关;否则,不算过关.能过第二关的概率是( ).
A. B. C. D.
4.在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )
A.M=N-1或M=N+1 B.M=N-1或M=N+2
C.M=N或M=N+1 D.M=N或M=N-1
5.如图,二次函数 的图象与x轴交于点A(-2,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线 .有下列结论:① ;② ;③ ;④ .其中正确的( )
A.①② B.①③ C.①④ D.③④
6.一个长8厘米,宽7厘米,高6厘米的长方体容器平放在桌面,里面盛有高2厘米的水(如图一); 将这个长方体沿着一条宽旋转90°,平放在桌面(如图二). 在旋转的过程中,水面的高度最高可以达到 ( )
A.厘米 B.4厘米 C.3厘米 D.厘米
7.如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若,.以下结论正确的个数是( )
①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为.
A.2个 B.3个 C.4个 D.5个
8. 如图,在矩形和矩形中,,且,连接交于点,连接交于点,交于点,则下列结论不正确的是( )
A.
B.当时,
C.当时,∽
D.当时,
9.如图,抛物线y= x2﹣1与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是( )
A. B. C.3 D.2
10.如图,在中,,,.动点从点出发,以的速度沿射线匀速运动,到点停止运动,同时动点从点出发,以的速度沿射线匀速运动.当点停止运动时,点也随之停止运动.在的右侧以为边作菱形,点在射线.设点的运动时间为,菱形与的重叠部分的面积为,则能大致反映与之间函数关系的图象是( )
A.B.C.D.
二、填空题
11.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 (结果保留π).
12.从位男同学和位女同学中任选人参加志愿者活动,所选人中恰好是一位男同学和一位女同学的概率是 .
13.已知函数y= ,若使y=k成立的x的值恰好有三个,则k的值为 .
14.二次函数y=x2+bx的对称轴为x=1,若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是 .
15.已知:如图,AD、CE分别是△ABC的角平分线和中线,AD⊥CE,AD=CE=4,则BC的长等于 .
16.在平面直角坐标系中,二次函数 (k为常数)与反比例函数 ( )的图象如图所示, , 是反比例函数图象上的两点,记P、Q两点间的部分为 ,
(1)当 时,二次函数的对称轴为 ;
(2) ;
(3)若二次函数的图象与 有两个公共点,则k的取值范围是 .
三、解答题
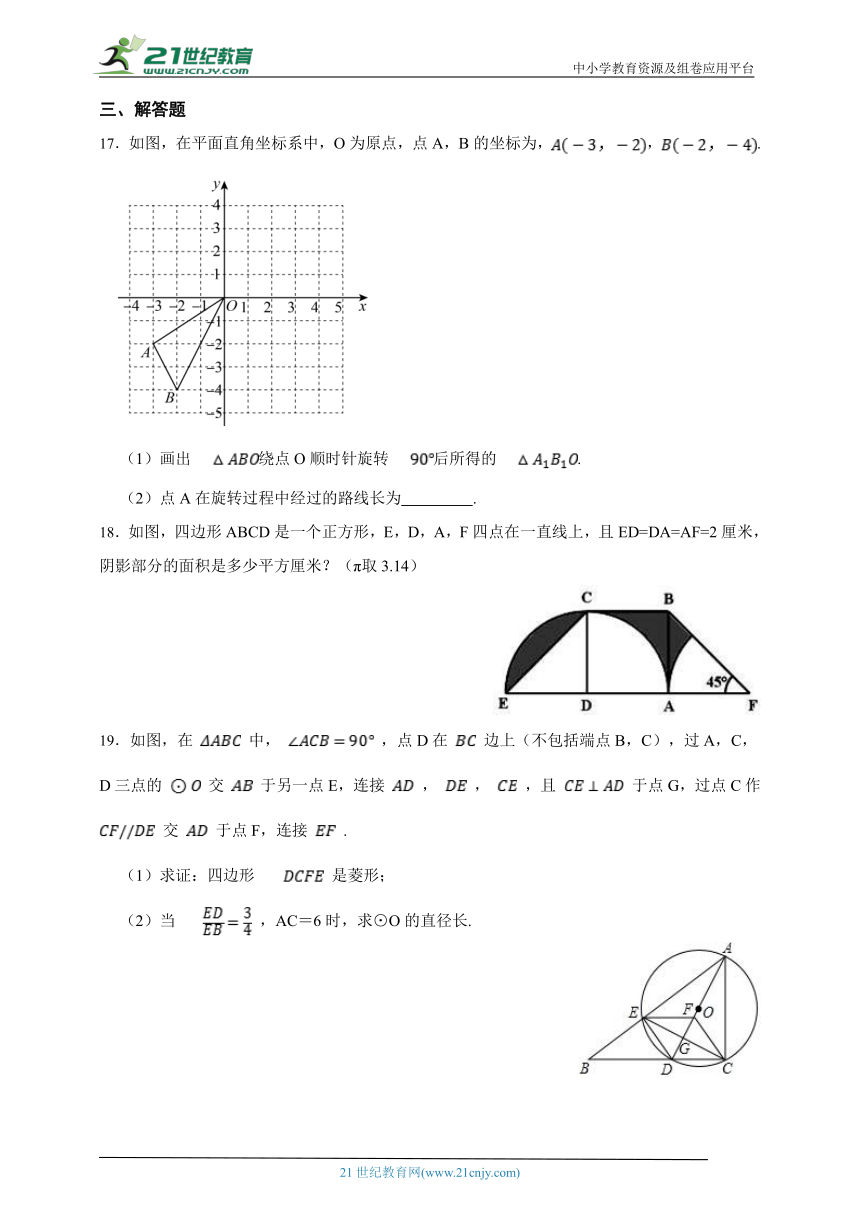
17.如图,在平面直角坐标系中,O为原点,点A,B的坐标为,,.
(1)画出绕点O顺时针旋转后所得的.
(2)点A在旋转过程中经过的路线长为 .
18.如图,四边形ABCD是一个正方形,E,D,A,F四点在一直线上,且ED=DA=AF=2厘米,阴影部分的面积是多少平方厘米?(π取3.14)
19.如图,在 中, ,点D在 边上(不包括端点B,C),过A,C,D三点的 交 于另一点E,连接 , , ,且 于点G,过点C作 交 于点F,连接 .
(1)求证:四边形 是菱形;
(2)当 ,AC=6时,求⊙O的直径长.
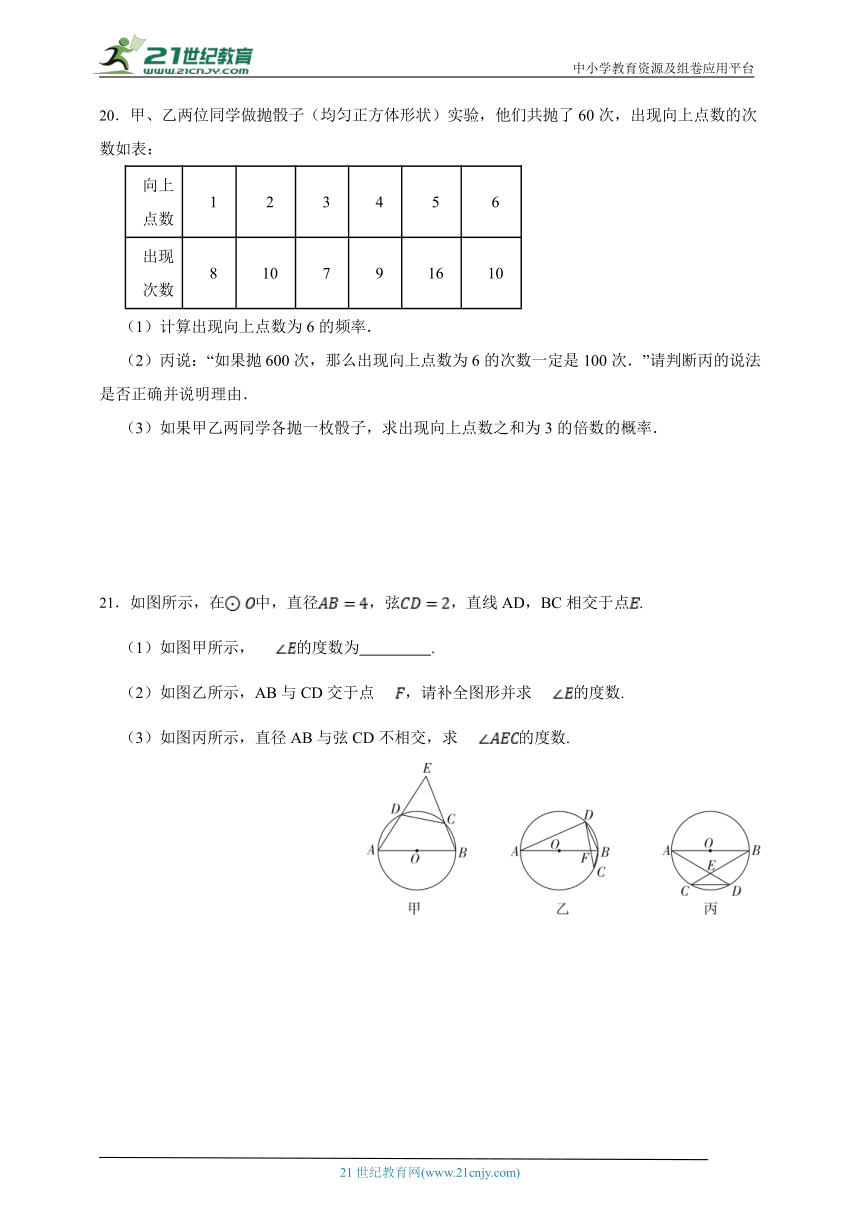
20.甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 1 2 3 4 5 6
出现次数 8 10 7 9 16 10
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
21.如图所示,在中,直径,弦,直线AD,BC相交于点.
(1)如图甲所示,的度数为 .
(2)如图乙所示,AB与CD交于点,请补全图形并求的度数.
(3)如图丙所示,直径AB与弦CD不相交,求的度数.
22.如图,在正方形中,点在对角线上,连接,,延长交于点,交的延长线于点.
(1)求证:.
(2)若,且,求正方形的边长.
(3)若,求的值.
2
3.如图,四边形ABCD是正方形,点M在BC上,点N在CD的延长线上,,连接AM,AN,点H在BC的延长线上,,点E在线段BH上,且,将线段EH绕点E逆时针旋转得到线段EG,使得,EG交AH于点
(1)线段AM与线段AN的关系是 .
(2)若,,求AH的长.
(3)求证:
24.如图,在直角坐标系中有,为坐标原点,,,将此三角形绕原点顺时针旋转,得到,二次函数的图象刚好经过,,三点.
(1)求二次函数的解析式及顶点的坐标;
(2)过定点的直线与二次函数图象相交于M,两点.
①若,求的值;
②证明:无论为何值,恒为直角三角形;
③当直线绕着定点旋转时,外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
答案解析部分
1.【答案】C
【解析】【解答】解:∵y=x2-4x+2=(x-2)2-2,
∴当-1≤x≤1时,y随x的增大而减小,
∴当x=1时,y取得最小值,最小值为-1.
故答案为:C.
【分析】根据二次函数的性质可得:当-1≤x≤1时,y随x的增大而减小,则函数在x=1处取得最小值,据此计算.
2.【答案】D
【解析】【解答】解:∵CC′∥AB,
∴∠ACC′=∠CAB=66°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,∠CAC′=∠BAB′
∴∠CAC′=180°-2∠ACC′=180°-2×66°=48°,
∴∠CAC′=∠BAB′=48°.
故答案为:D.
【分析】由平行线的性质可得∠ACC′=∠CAB=66°,由旋转的性质可得AC=AC′,∠CAC′=∠BAB′,利用等腰三角形的性质及三角形的内角和求出∠CAC′=48°,即得结论.
3.【答案】A
【解析】【解答】解: ∵在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,n次抛掷所出现的点数之和大于则算过关;
∴能过第二关的抛掷所出现的点数之和需要大于5,
列表得:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
∵共有36种等可能的结果,能过第二关的有26种情况,
∴能过第二关的概率是:
故选:A.
【分析】将n用2代入,求出能过第二关所出现的点数之和需要大于的值,再列出表格,得出所有可能的结果数和能过第二关的结果数,利用概率公式求解.
4.【答案】C
【解析】【解答】解:∵y=(x+a)(x+b),
∴函数图象与x轴交点坐标为 :(-a,0),(-b,0),
又∵y=(ax+1)(bx+1),
∴函数图象与x轴交点坐标为 :(- ,0),(- ,0),
∵a≠b,
∴M=N,或M=N+1.
故答案为:C.
【分析】根据函数解析式分别得出图像与x轴的交点坐标,根据题意a≠b分等于0和不等于0的情况即可得出两个交点个数之间的关系式,从而得出答案.
5.【答案】B
【解析】【解答】解:①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点在(0, 2)和(0, 1)之间,
∴a>0, =1, 2<c< 1,
∴b<0,abc>0,结论①正确;
②∵抛物线与x轴交于点A( 2,0),对称轴为直线x=1,
∴抛物线与x轴的另一交点坐标为(4,0),
∴当x=2时,y=4a+2b+c<0,结论②错误;
③当x= 2时,y=4a 2b+c=0,
∴4a 2b= c.
∵b= 2a,
∴8a= c.
又∵ 2<c< 1,
∴ ,结论③正确;
④∵当x= 1时,y=a b+c<0,a>0,
∴ b+c<0,
∴b>c,结论④错误.
综上所述:正确的结论有①③.
故答案为:B.
【分析】①由抛物线的开口方向、对称轴以及与y轴的交点,可得出a>0、b<0、c<0,进而可得出abc>0,即可判断①;
②由抛物线的对称轴及点A的坐标,可得出抛物线与x轴的另一交点坐标,结合抛物线的开口可得出当x=2时,y=4a+2b+c<0,即可判断②;
③由当x= 2时y=4a 2b+c=0,结合b= 2a可得出8a= c,再根据 2<c< 1,即可求出18<a<14;即可判断④;
④由a b+c<0、a>0,可得出 b+c<0,即b>c,即可判断④.
6.【答案】B
【解析】【解答】由题意知,水的体积为8×7×2=112(cm3)
如下图,过点E作EH⊥CD垂足为H,为使得在旋转过程,其水面高FH最大,水的体积应集中在该立方体左下角,其立体图形可视作四棱锥(以四边形ABCD为底面,高为EH);也可视作为三棱柱(以△CDE为底面,高为EF),
此时,EF保持不变,故将该立体图形视作三棱柱,即高EF=7保持不变,则,
设CE=a,DE=b,(a<7)则有
∴在Rt△CDE中,,
∴ab=32,.
∴当且仅当,a=b=时,.
故选:B
【分析】需分析在旋转,即立体图形斜放时,水体积在立体图形左下侧时最大, 画出示意图,易发现该图形试卷为三棱柱或三棱锥,当保持绕宽旋转时,此时分析其中的变量与不变量,进而将几何问题用代数表示出来,进而利用配方法求出该最大值.
7.【答案】C
【解析】【解答】解:∵AF⊥x轴,
∴∠AFE=∠BOE=90°,
∵∠OEB=∠AEF,
∴△AEF∽△BEO,
∴,∠EAF=∠OBE,
∴BO=3AF,
∵四边形ABCD是矩形,
∴AO=CO=BO=DO,
∴AO=3AF,∠OBA=∠OAB,故①正确;
∴∠OAB=∠EAF,
∴AE平分∠OAF,故②正确;
∵OE=3,EF=1,
∴OF=4,
∵OA2 AF2=OF2,
∴8AF2=16,
∴(取正值),
∴点A坐标为,
∵点A,点C关于原点对称,
∴点C,故③正确;
∵,OA=3AF,
∴,
∴,故④错误;
∵
∴矩形ABCD的面积,故⑤正确;
∴正确的个数有4个.
故答案为:C.
【分析】利用垂直的定义和对顶角相等,可证得∠AFE=∠BOE,∠OEB=∠AEF,可得到△AEF∽△BEO,利用相似三角形的性质可得到BO=3AF,∠EAF=∠OBE,利用矩形的性质可推出AO=CO=BO=DO,可对①作出判断;同时利用等腰三角形的性质可知∠OBA=∠OAB,可推出∠OAB=∠EAF,可对②作出判断;再利用勾股定理求出AF的长,可得到点A的坐标,利用关于原点对称点的坐标特点:横纵坐标都互为相反数,可得到点C的坐标,可对③作出判断;利用OA=3AF,可求出BD的长,可对④作出判断;然后求出BD的长,利用三角形的面积公式求出△ABD的面积,即可求出矩形ABCD的面积,可对⑤作出判断;综上所述,可得到正确结论的个数
8.【答案】C
【解析】【解答】解:、四边形和四边形是矩形,
,
,
.
又,
∽,
.
,,
,故A正确;
B、,
,
.
,
∽,
,
.
,
,
故B正确;
C、当时,
,
,
不能判定∽,
故C错误;
D、如图,过点分别作于点,交的延长线于点,设.
,
.
,
,
,
,
,
,
,
故D正确,
故选:.
【分析】利用相似三角形的判定方法证出∽,可得,再利用角的运算和等量代换可得,可证出A正确;再证出∽,可得,再利用等量代换证出即可判断B正确;根据无法判断∽,即可判断出C是否正确;过点分别作于点,交的延长线于点,先求出,,再求出即可判断D正确.
9.【答案】D
【解析】【解答】解:令y= x2﹣1=0,则x=±3,
故点B(3,0),
设圆的半径为r,则r=1,
当B、D、C三点共线,且点D在BC之间时,BD最小,
而点E、O分别为AD、AB的中点,故OE是△ABD的中位线,
则OE= BD= (BC﹣r)= ( ﹣1)=2,
故答案为:D.
【分析】当B、D、C三点共线,且点D在BC之间时,BD最小,而OE是△ABD的中位线,即可求解.
10.【答案】A
【解析】【解答】解:将菱形PQMN平移的过程,分几个过程:
(1)当菱形PQMN整个都在△ABC内部,即重叠部分面积为菱形PQMN的全部面积.
作PD⊥AC于D,QE⊥AB于E,
设AP=x,AQ=
∵∠A=30°,∴在Rt△ADP中,,
所以D为AQ的中点,即PD垂直平分AQ,即AQ=AP=x
而在Rt△AQE中,∵∠A=30°,
所以此时
因此第一段为一个抛物线函数,开口向上,B选项错误,排除;
特别地,当M点运动到BC上时,如图,
∵∠ABC=60°,在(1)的条件下,∵MN∥QP,∠QPN=60°,∴∠MNB=60°=∠MBN
∴△MNB为等边三角形,∴MN=NB,,
综上所述,当0<x≤1时,
(2)当菱形开始部分和△ABC有重叠时,形成五边形FGNPQ,
作GH⊥FM,如下图所示,
则S五边形FGNPQ=S菱形PNMQ-S△FGM
同理(1),∵△NGB和△FGM均为等边三角形,NB=AB-AP-PN=3-2x
∴NG=3-2x,MG=MN-NG=x-(3-2x)=3x-3=MF
∴
∴
∴
∴
∵a<0,所以此段抛物线开口向下,C、D选项不符合题意,排除;
特别地,当F、G分别和Q、N重合时,如图,
此时,AP+PN=AB,即2x=3,所以x=1.5,
∴综上所述,当1≤x≤1.5时,
(3)当1.5≤x≤3时,如图所示,
重叠部分为△PEB的面积,作EF⊥AB于点F.
∵PB=3-x,△PEB为等边三角形
则,∴
∴
因为a>0,所以这段抛物线开口向上,
综上所述,重叠部分面积y与x的函数关系式分别是三段抛物线组成,开口依次朝上,朝下,朝上,符合的只有A,故答案选A.
【分析】因为当P、Q运动过程中,菱形的不同位置,导致和△ABC的重叠图形形状不同,因此需要分类讨论作图:三类情况分别是重叠部分依次为(1)整个菱形,(2)五边形,(3)三角形.菱形的计算直接采用“底×高”的方法计算,五边形的计算采用“割补法”,用“菱形的面积减去未重叠的三角形面积”,三角形的面积直接用“底×高×0.5”计算.在计算过程中,要充分利用含(构造)30°的特殊三角形的三边比例关系,即,在计算过程中能简化计算过程.
11.【答案】
【解析】【解答】解:根据图示知,∠1+∠2=180°﹣90°﹣45°=45°,
∵∠ABC+∠ADC=180°,
∴图中阴影部分的圆心角的和是90°+90°﹣∠1﹣∠2=135°,
∴阴影部分的面积应为:S=.
故答案是:.
【分析】阴影部分可看成是圆心角为135°,半径为1是扇形.
12.【答案】
【解析】【解答】解:根据题意画树状图:
∵共有20种可能的结果,所选2人中恰好是一位男同学和一位女同学的情况有12种,
∴所选2人中恰好是一位男同学和一位女同学的概率为:= ,
故答案为
【分析】先利用树状图求出所有等可能的情况数,再利用概率公式求解即可。
13.【答案】1或2
【解析】【解答】解:函数y= 的图象如图:
根据图象知道当y=1或2时,对应成立的x值恰好有三个,
∴k=1或2.
故答案为1或2.
【分析】首先在坐标系中画出已知函数y= 的图像,利用数形结合的方法即可找到Y=K 成立的X值恰好有三个的k值。
14.【答案】﹣1≤t<8
【解析】【解答】解:对称轴为直线x=﹣ =1,
解得b=﹣2,
∴二次函数解析式为y=x2﹣2x,即y=(x﹣1)2﹣1,
x=﹣1时,y=1+2=3,
x=4时,y=16﹣2×4=8,
y=(x﹣1)2﹣1的最小值是﹣1,
∵x2+bx﹣t=0相当于y=x2+bx与直线y=t的交点的横坐标,如下图所示
∴当﹣1≤t<8时,在﹣1<x<4的范围内有解.
故答案为:﹣1≤t<8.
【分析】根据对称轴求出b的值,从而得到x=﹣1、4时的函数值,再根据一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解相当于y=x2+bx与y=t在x的范围内有交点解答.
15.【答案】
【解析】【解答】如下图,过点B作CE的垂线,交CE延长线于点F,AD与CE交于点H.
∵AD⊥EC,AD是∠EAC的角平分线
∴∠EAH=∠HAC
∴∠AEH=∠ACH,∴AE=AC,△AEC是等腰三角形
∵CE=4
∴EH=HC=2
∵CE是△ABC的中线,∴AE=EB
∵∠AEH=∠FEB,∠AHE=∠BFE=90°
∴△AEH≌△BEF
∴EF=2,FC=2+2+2=6,BF=AH
∵∠DCH=∠BCF,∠DHC=∠BFC=90°
∴△DCH∽△BCF
∴
∴3DH=BF,∴3DH=HA
∵AD=4
∴HD=1,FB=3
∴在Rt△CBF中,CB=
故答案为:
【分析】如下图,过点B作CE的垂线,交CE延长线于点F,先证△BFE≌△AHE,然后利用AD⊥CE可得FE、EH、HC的长,接着证△BFE∽△DHC,利用线段比的关系可求得BC的长.
16.【答案】(1)
(2)-3
(3)
【解析】【解答】解:(1)对于二次函数 ,
对称轴为 ,
当 时,二次函数的对称轴为 ;
故答案为: ;
(2)∵反比例函数 的图象过点P(2,y1),
∴ ,
故答案为: ;
(3)同(2)求得点P(2, ),Q(6, ),
如图,当二次函数的对称轴在P、Q两点之间时,二次函数的图象与PQ才有两个公共点,
∴ ,
当 时, ,
解方程: ,得 (舍去),
当 时, ,
解方程: ,得 (舍去),
则k的取值范围是 .
故答案为: .
【分析】(1)二次函数的对称轴为 ,代入数据即可求解;
(2)把点P(2,y1)代入 即可求解;
(3)根据题意知二次函数的对称轴在P、Q两点之间时,二次函数的图象与PQ才有两个公共点,当 或 时,二次函数的值应该小于或等于反比例函数的值,二次函数的图象与PQ才有两个公共点,据此求解即可.
17.【答案】(1)解:如图,即为所求作;
(2)
【解析】【解答】解:(2)如图,,
∴点A在旋转过程中经过的路线长为,
故答案为:.
【分析】(1)利用方格纸的特点及旋转的性质,结合旋转的方向和角度,分别作出但A、B绕点O顺时针旋转90°后的对应点A1、B1,再顺次连接A1、B1、O即可;
(2)利用勾股定理算出OA的长,进而根据弧长计算公式“”计算即可.
18.【答案】解:S阴=S正-S扇+S扇-S△+S△-S小扇
S阴=S正-S小扇
S阴=22-
答:阴影部分的面积是2.43平方厘米。
【解析】【分析】三角形CDE和三角形BAF是完全一样的等腰直角三角形,阴影部分的面积=正方形的面积-最右边扇形的面积;其中,正方形的面积=边长×边长,扇形的面积=π×半径2×45° ÷360°。
19.【答案】(1)证明:已知 ,
∴ 为直径,
∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴四边形 为平行四边形,
又∵ ,
∴四边形 是菱形;
(2)解:∵ , ,
∴ ,
∵四边形 内接于 ,
∴
∵ 四边形 是菱形,
∴ , ,
∵ ,
在 中,设 ,则 ,
∴ , ,
∵ ,
∴ ,
解得 或 (舍去),
∴ ,
∴在 中,
有 .
即 的直径长为 .
【解析】【分析】(1)由题意用角边角可证△DEG≌△FCG,则ED=FC,由一组对边平行且相等的四边形是平行四边形可得四边形DCFE为平行四边形,再根据对角线互相垂直的平行四边形是菱形可求解;
(2)在Rt△BED中,由已知的等式设DE=3a,则BE=4a,在Rt△ABC中用勾股定理可得关于a的方程,解方程即求得a的值;在Rt△ACD中用勾股定理求得AD的值即可.
20.【答案】解:(1)出现向上点数为6的频率=;
(2)丙的说法不正确,
理由:(1)因为实验次数较多时,向上点数为6的频率接近于概率,但不说明概率就等一定等于频率;
(2)从概率角度来说,向上点数为6的概率是的意义是指平均每6次出现1次;
(3)用表格列出所有等可能性结果:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
共有36种等可能性结果,其中点数之和为3的倍数可能性结果有12个
∴P(点数之和为3的倍数)==.
【解析】【分析】(1)直接利用概率公式求得概率即可;
(2)利用概率的意义分别分析后即可判断谁的说法正确;
(3)列表将所有等可能的结果列举出来,利用概率公式求解即可.
21.【答案】(1)
(2)解:连接OC、OD,
∵直径AB=4,CD=2,
∴OC=OD=CD=2,
∴△OCD是等边三角形,
∴∠COD=60°,
∴∠DAC=∠COD=30°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠E=90°-∠DAC=60°;
(3)解:如图,连接OC、OD、BD,
∵直径AB=4,CD=2,
∴OC=OD=CD=2,
∴△OCD是等边三角形,
∴∠COD=60°,
∴∠DBC=∠COD=30°,
∵AB是圆O的直径,
∴∠ADB=90°,
∴∠E=90°-∠DBC=60°.
【解析】【解答】解:(1)如图,连接OC、OD、BD,
∵直径AB=4,CD=2,
∴OC=OD=CD=2,
∴△OCD是等边三角形,
∴∠COD=60°,
∴∠DBC=∠COD=30°,
∵AB是圆O的直径,
∴∠ADB=90°=∠BDE,
∴∠E=90°-∠DBC=60°;
故答案为:60°;
【分析】(1)连接OC、OD、BD,由三边相等的三角形是等边三角形可得△OCD是等边三角形,由等边三角形的性质及同弧所对的圆周角等于圆心角的一半得∠DBC=∠COD=30°,由直径所对的圆周角是直角得∠ADB=90°=∠BDE,最后根据直角三角形的两锐角互余可算出∠E的度数;
(2)连接OC、OD,由三边相等的三角形是等边三角形可得△OCD是等边三角形,由等边三角形的性质及同弧所对的圆周角等于圆心角的一半得∠DAC=∠COD=30°,由直径所对的圆周角是直角得∠ACB=90°,最后根据直角三角形的两锐角互余可算出∠E的度数;
(3)连接OC、OD、BD,由三边相等的三角形是等边三角形可得△OCD是等边三角形,由等边三角形的性质及同弧所对的圆周角等于圆心角的一半得∠DBC=∠COD=30°,由直径所对的圆周角是直角得∠ADB=90°,最后根据直角三角形的两锐角互余可算出∠BED的度数,最后根据对顶角相等得出答案.
22.【答案】(1)证明:是正方形的对角线,
,,,
,
≌,
,
,
,
;
(2)解:,且,
,
由知,,
,
四边形是正方形,
,,,
,
,
,
≌,
,
,
,
,
,
设正方形的边长为,
,
,
在中,,
,
或舍去,
正方形的边长为;
(3)解:如图,过点作交于点,
由知,≌,
,,
,,
,
,
,
,
,,,
,
,
,
,
,,
,,
,
,
∽,
,
.
【解析】【分析】(1)通过边角边证明≌,得到,再利用两平行直线之间内错角相等得到,进而得到;
(2)根据等边对等角和三角形外角性质得,进而推得,再利用勾股定理和含角的性质求正方形的边长;
(3)过点作交于点,结合(1)知≌,利用等角对等边证明,,根据得到,由得到∽,进而求 的值.
23.【答案】(1)垂直且相等
(2)解:,,
∽,
,
线段EH绕点E逆时针旋转得到线段EG,
,
,
,
;
(3)证明:如图,
延长MB至X,连接AX,使BX=BM,作∠AMR=∠H,交AX于R,
,
,
,
,,
设∠XAB=∠BAM=,
,,
,
,
,
,
,,,
≌,
【解析】【解答】解:(1)∵四边形ABCD是正方形,
∴∠BAD=∠ADN=∠ADC=∠B=90°,AD=AB,
又∵BM=DN,
∴△ABM≌△ADN(SAS),
∴AM=AN,∠BAM=∠DAN,
∴∠MAN=∠DAN+∠MAD=∠BAM+∠MAD=∠BAD=90°,
∴AM⊥AN,
故答案为:垂直且相等;
【分析】(1)由正方形性质得∠BAD=∠ADN=∠ADC=∠B=90°,AD=AB,结合已知,由SAS判断出△ABM≌△ADN,由全等三角形的性质得AM=AN,∠BAM=∠DAN,进而根据角的和差及等量代换可得∠MAN=90°,从而可得结论;
(2)首先由有两组角对应相等的两个三角形相似得△HEF∽△HAM,由相似三角形的对应边成比例建立方程可求出AH的长;
(3)延长MB至X,连接AX,使BX=BM,作∠AMR=∠H,交AX于R,由线段垂直平分线的性质得AX=AM,由等腰三角形性质得∠XAB=∠BAM,∠X=∠AMB,设∠XAB=∠BAM=,根据已知、三角形的内角和定理、三角形外角和定理推出∠X=∠MRX,由等角对等边得RM=XM,然后用ASA判断出△HEF≌△MAR,由全等三角形的对应边相等可得结论.
24.【答案】(1)解:∵A(0,3),B(-1,0),
∴OA=3,OB=1,
根据旋转的性质得OC=OA=3,
∴C(3,0),
把A(0,3),B(-1,0),C(3,0),分别代入y=ax2+bx+c得
,
解得,
∴二次函数的解析式为:y=-x2+2x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点P的坐标为(1,4);
(2)解:①设,
直线:过定点,抛物线的顶点坐标为,
,
,
,
联立
得,
,
,
;
②证明:过点作轴,垂足为,分别过点,作的垂线,垂足分别为、,
设.
,在二次函数图象上,
,.
,
,,,,
,
,
由①可知,
,
,
,
,
,
,
,即,
无论为何值,恒为直角三角形;
③
【解析】【解答】解:(2)③∵恒为直角三角形,,
∴外接圆圆心是线段的中点;
设线段的中点,
∵,,.
∴
∴的中点为,
,
化简,得,
抛物线的表达式为.
【分析】(1)根据点A、B的坐标可得OA、OB的长,根据旋转的性质可得OC=OA,从而得出点C的坐标,然后利用待定系数法求抛物线的解析式,再将解析式配成顶点式可得点点P的坐标;
(2)①设M(x1,y1),N(x2,y2),易得定点Q为(1,3),则PQ=1,根据三角形面积公式得x2-x1=4,联立抛物线与直线的解析式得x2+(k-2)x-k=0,由根与系数的关系得x1+x2=2-k,x2x1=-k,再利用完全平方公式的恒等变形可得关于字母k的方程,求解即可;
② 过P作PG⊥x轴于G,过M,N作PG的垂线,垂足分别为E、F, 设M(x1,y1),N(x2,y2),根据两点间的距离公式表示出PE、ME、PF、NF,由正切函数的定义得tan∠PME=1-x1, , 然后根据根与系数的关系及等角的同名三角函数值相等证明∠PME=∠FPN,据此即可证得结论;
③根据圆周角定理得Rt△PMN外接圆的圆心是线段MN的中点;根据中点坐标公式计算即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九上期末提升卷(含解析)
一、单选题
1.已知二次函数,当时,y的最小值为( )
A. B. C. D.7
2.如图,在△ABC中,∠CAB=66°.在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'的度数为( )
A.70° B.50° C.40° D.48°
3.一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6个点)抛掷n次,若n次抛掷所出现的向上一面的点数之和大于n2,则算过关;否则,不算过关.能过第二关的概率是( ).
A. B. C. D.
4.在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )
A.M=N-1或M=N+1 B.M=N-1或M=N+2
C.M=N或M=N+1 D.M=N或M=N-1
5.如图,二次函数 的图象与x轴交于点A(-2,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线 .有下列结论:① ;② ;③ ;④ .其中正确的( )
A.①② B.①③ C.①④ D.③④
6.一个长8厘米,宽7厘米,高6厘米的长方体容器平放在桌面,里面盛有高2厘米的水(如图一); 将这个长方体沿着一条宽旋转90°,平放在桌面(如图二). 在旋转的过程中,水面的高度最高可以达到 ( )
A.厘米 B.4厘米 C.3厘米 D.厘米
7.如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若,.以下结论正确的个数是( )
①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为.
A.2个 B.3个 C.4个 D.5个
8. 如图,在矩形和矩形中,,且,连接交于点,连接交于点,交于点,则下列结论不正确的是( )
A.
B.当时,
C.当时,∽
D.当时,
9.如图,抛物线y= x2﹣1与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是( )
A. B. C.3 D.2
10.如图,在中,,,.动点从点出发,以的速度沿射线匀速运动,到点停止运动,同时动点从点出发,以的速度沿射线匀速运动.当点停止运动时,点也随之停止运动.在的右侧以为边作菱形,点在射线.设点的运动时间为,菱形与的重叠部分的面积为,则能大致反映与之间函数关系的图象是( )
A.B.C.D.
二、填空题
11.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 (结果保留π).
12.从位男同学和位女同学中任选人参加志愿者活动,所选人中恰好是一位男同学和一位女同学的概率是 .
13.已知函数y= ,若使y=k成立的x的值恰好有三个,则k的值为 .
14.二次函数y=x2+bx的对称轴为x=1,若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是 .
15.已知:如图,AD、CE分别是△ABC的角平分线和中线,AD⊥CE,AD=CE=4,则BC的长等于 .
16.在平面直角坐标系中,二次函数 (k为常数)与反比例函数 ( )的图象如图所示, , 是反比例函数图象上的两点,记P、Q两点间的部分为 ,
(1)当 时,二次函数的对称轴为 ;
(2) ;
(3)若二次函数的图象与 有两个公共点,则k的取值范围是 .
三、解答题
17.如图,在平面直角坐标系中,O为原点,点A,B的坐标为,,.
(1)画出绕点O顺时针旋转后所得的.
(2)点A在旋转过程中经过的路线长为 .
18.如图,四边形ABCD是一个正方形,E,D,A,F四点在一直线上,且ED=DA=AF=2厘米,阴影部分的面积是多少平方厘米?(π取3.14)
19.如图,在 中, ,点D在 边上(不包括端点B,C),过A,C,D三点的 交 于另一点E,连接 , , ,且 于点G,过点C作 交 于点F,连接 .
(1)求证:四边形 是菱形;
(2)当 ,AC=6时,求⊙O的直径长.
20.甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 1 2 3 4 5 6
出现次数 8 10 7 9 16 10
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
21.如图所示,在中,直径,弦,直线AD,BC相交于点.
(1)如图甲所示,的度数为 .
(2)如图乙所示,AB与CD交于点,请补全图形并求的度数.
(3)如图丙所示,直径AB与弦CD不相交,求的度数.
22.如图,在正方形中,点在对角线上,连接,,延长交于点,交的延长线于点.
(1)求证:.
(2)若,且,求正方形的边长.
(3)若,求的值.
2
3.如图,四边形ABCD是正方形,点M在BC上,点N在CD的延长线上,,连接AM,AN,点H在BC的延长线上,,点E在线段BH上,且,将线段EH绕点E逆时针旋转得到线段EG,使得,EG交AH于点
(1)线段AM与线段AN的关系是 .
(2)若,,求AH的长.
(3)求证:
24.如图,在直角坐标系中有,为坐标原点,,,将此三角形绕原点顺时针旋转,得到,二次函数的图象刚好经过,,三点.
(1)求二次函数的解析式及顶点的坐标;
(2)过定点的直线与二次函数图象相交于M,两点.
①若,求的值;
②证明:无论为何值,恒为直角三角形;
③当直线绕着定点旋转时,外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
答案解析部分
1.【答案】C
【解析】【解答】解:∵y=x2-4x+2=(x-2)2-2,
∴当-1≤x≤1时,y随x的增大而减小,
∴当x=1时,y取得最小值,最小值为-1.
故答案为:C.
【分析】根据二次函数的性质可得:当-1≤x≤1时,y随x的增大而减小,则函数在x=1处取得最小值,据此计算.
2.【答案】D
【解析】【解答】解:∵CC′∥AB,
∴∠ACC′=∠CAB=66°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,∠CAC′=∠BAB′
∴∠CAC′=180°-2∠ACC′=180°-2×66°=48°,
∴∠CAC′=∠BAB′=48°.
故答案为:D.
【分析】由平行线的性质可得∠ACC′=∠CAB=66°,由旋转的性质可得AC=AC′,∠CAC′=∠BAB′,利用等腰三角形的性质及三角形的内角和求出∠CAC′=48°,即得结论.
3.【答案】A
【解析】【解答】解: ∵在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,n次抛掷所出现的点数之和大于则算过关;
∴能过第二关的抛掷所出现的点数之和需要大于5,
列表得:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
∵共有36种等可能的结果,能过第二关的有26种情况,
∴能过第二关的概率是:
故选:A.
【分析】将n用2代入,求出能过第二关所出现的点数之和需要大于的值,再列出表格,得出所有可能的结果数和能过第二关的结果数,利用概率公式求解.
4.【答案】C
【解析】【解答】解:∵y=(x+a)(x+b),
∴函数图象与x轴交点坐标为 :(-a,0),(-b,0),
又∵y=(ax+1)(bx+1),
∴函数图象与x轴交点坐标为 :(- ,0),(- ,0),
∵a≠b,
∴M=N,或M=N+1.
故答案为:C.
【分析】根据函数解析式分别得出图像与x轴的交点坐标,根据题意a≠b分等于0和不等于0的情况即可得出两个交点个数之间的关系式,从而得出答案.
5.【答案】B
【解析】【解答】解:①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点在(0, 2)和(0, 1)之间,
∴a>0, =1, 2<c< 1,
∴b<0,abc>0,结论①正确;
②∵抛物线与x轴交于点A( 2,0),对称轴为直线x=1,
∴抛物线与x轴的另一交点坐标为(4,0),
∴当x=2时,y=4a+2b+c<0,结论②错误;
③当x= 2时,y=4a 2b+c=0,
∴4a 2b= c.
∵b= 2a,
∴8a= c.
又∵ 2<c< 1,
∴ ,结论③正确;
④∵当x= 1时,y=a b+c<0,a>0,
∴ b+c<0,
∴b>c,结论④错误.
综上所述:正确的结论有①③.
故答案为:B.
【分析】①由抛物线的开口方向、对称轴以及与y轴的交点,可得出a>0、b<0、c<0,进而可得出abc>0,即可判断①;
②由抛物线的对称轴及点A的坐标,可得出抛物线与x轴的另一交点坐标,结合抛物线的开口可得出当x=2时,y=4a+2b+c<0,即可判断②;
③由当x= 2时y=4a 2b+c=0,结合b= 2a可得出8a= c,再根据 2<c< 1,即可求出18<a<14;即可判断④;
④由a b+c<0、a>0,可得出 b+c<0,即b>c,即可判断④.
6.【答案】B
【解析】【解答】由题意知,水的体积为8×7×2=112(cm3)
如下图,过点E作EH⊥CD垂足为H,为使得在旋转过程,其水面高FH最大,水的体积应集中在该立方体左下角,其立体图形可视作四棱锥(以四边形ABCD为底面,高为EH);也可视作为三棱柱(以△CDE为底面,高为EF),
此时,EF保持不变,故将该立体图形视作三棱柱,即高EF=7保持不变,则,
设CE=a,DE=b,(a<7)则有
∴在Rt△CDE中,,
∴ab=32,.
∴当且仅当,a=b=时,.
故选:B
【分析】需分析在旋转,即立体图形斜放时,水体积在立体图形左下侧时最大, 画出示意图,易发现该图形试卷为三棱柱或三棱锥,当保持绕宽旋转时,此时分析其中的变量与不变量,进而将几何问题用代数表示出来,进而利用配方法求出该最大值.
7.【答案】C
【解析】【解答】解:∵AF⊥x轴,
∴∠AFE=∠BOE=90°,
∵∠OEB=∠AEF,
∴△AEF∽△BEO,
∴,∠EAF=∠OBE,
∴BO=3AF,
∵四边形ABCD是矩形,
∴AO=CO=BO=DO,
∴AO=3AF,∠OBA=∠OAB,故①正确;
∴∠OAB=∠EAF,
∴AE平分∠OAF,故②正确;
∵OE=3,EF=1,
∴OF=4,
∵OA2 AF2=OF2,
∴8AF2=16,
∴(取正值),
∴点A坐标为,
∵点A,点C关于原点对称,
∴点C,故③正确;
∵,OA=3AF,
∴,
∴,故④错误;
∵
∴矩形ABCD的面积,故⑤正确;
∴正确的个数有4个.
故答案为:C.
【分析】利用垂直的定义和对顶角相等,可证得∠AFE=∠BOE,∠OEB=∠AEF,可得到△AEF∽△BEO,利用相似三角形的性质可得到BO=3AF,∠EAF=∠OBE,利用矩形的性质可推出AO=CO=BO=DO,可对①作出判断;同时利用等腰三角形的性质可知∠OBA=∠OAB,可推出∠OAB=∠EAF,可对②作出判断;再利用勾股定理求出AF的长,可得到点A的坐标,利用关于原点对称点的坐标特点:横纵坐标都互为相反数,可得到点C的坐标,可对③作出判断;利用OA=3AF,可求出BD的长,可对④作出判断;然后求出BD的长,利用三角形的面积公式求出△ABD的面积,即可求出矩形ABCD的面积,可对⑤作出判断;综上所述,可得到正确结论的个数
8.【答案】C
【解析】【解答】解:、四边形和四边形是矩形,
,
,
.
又,
∽,
.
,,
,故A正确;
B、,
,
.
,
∽,
,
.
,
,
故B正确;
C、当时,
,
,
不能判定∽,
故C错误;
D、如图,过点分别作于点,交的延长线于点,设.
,
.
,
,
,
,
,
,
,
故D正确,
故选:.
【分析】利用相似三角形的判定方法证出∽,可得,再利用角的运算和等量代换可得,可证出A正确;再证出∽,可得,再利用等量代换证出即可判断B正确;根据无法判断∽,即可判断出C是否正确;过点分别作于点,交的延长线于点,先求出,,再求出即可判断D正确.
9.【答案】D
【解析】【解答】解:令y= x2﹣1=0,则x=±3,
故点B(3,0),
设圆的半径为r,则r=1,
当B、D、C三点共线,且点D在BC之间时,BD最小,
而点E、O分别为AD、AB的中点,故OE是△ABD的中位线,
则OE= BD= (BC﹣r)= ( ﹣1)=2,
故答案为:D.
【分析】当B、D、C三点共线,且点D在BC之间时,BD最小,而OE是△ABD的中位线,即可求解.
10.【答案】A
【解析】【解答】解:将菱形PQMN平移的过程,分几个过程:
(1)当菱形PQMN整个都在△ABC内部,即重叠部分面积为菱形PQMN的全部面积.
作PD⊥AC于D,QE⊥AB于E,
设AP=x,AQ=
∵∠A=30°,∴在Rt△ADP中,,
所以D为AQ的中点,即PD垂直平分AQ,即AQ=AP=x
而在Rt△AQE中,∵∠A=30°,
所以此时
因此第一段为一个抛物线函数,开口向上,B选项错误,排除;
特别地,当M点运动到BC上时,如图,
∵∠ABC=60°,在(1)的条件下,∵MN∥QP,∠QPN=60°,∴∠MNB=60°=∠MBN
∴△MNB为等边三角形,∴MN=NB,,
综上所述,当0<x≤1时,
(2)当菱形开始部分和△ABC有重叠时,形成五边形FGNPQ,
作GH⊥FM,如下图所示,
则S五边形FGNPQ=S菱形PNMQ-S△FGM
同理(1),∵△NGB和△FGM均为等边三角形,NB=AB-AP-PN=3-2x
∴NG=3-2x,MG=MN-NG=x-(3-2x)=3x-3=MF
∴
∴
∴
∴
∵a<0,所以此段抛物线开口向下,C、D选项不符合题意,排除;
特别地,当F、G分别和Q、N重合时,如图,
此时,AP+PN=AB,即2x=3,所以x=1.5,
∴综上所述,当1≤x≤1.5时,
(3)当1.5≤x≤3时,如图所示,
重叠部分为△PEB的面积,作EF⊥AB于点F.
∵PB=3-x,△PEB为等边三角形
则,∴
∴
因为a>0,所以这段抛物线开口向上,
综上所述,重叠部分面积y与x的函数关系式分别是三段抛物线组成,开口依次朝上,朝下,朝上,符合的只有A,故答案选A.
【分析】因为当P、Q运动过程中,菱形的不同位置,导致和△ABC的重叠图形形状不同,因此需要分类讨论作图:三类情况分别是重叠部分依次为(1)整个菱形,(2)五边形,(3)三角形.菱形的计算直接采用“底×高”的方法计算,五边形的计算采用“割补法”,用“菱形的面积减去未重叠的三角形面积”,三角形的面积直接用“底×高×0.5”计算.在计算过程中,要充分利用含(构造)30°的特殊三角形的三边比例关系,即,在计算过程中能简化计算过程.
11.【答案】
【解析】【解答】解:根据图示知,∠1+∠2=180°﹣90°﹣45°=45°,
∵∠ABC+∠ADC=180°,
∴图中阴影部分的圆心角的和是90°+90°﹣∠1﹣∠2=135°,
∴阴影部分的面积应为:S=.
故答案是:.
【分析】阴影部分可看成是圆心角为135°,半径为1是扇形.
12.【答案】
【解析】【解答】解:根据题意画树状图:
∵共有20种可能的结果,所选2人中恰好是一位男同学和一位女同学的情况有12种,
∴所选2人中恰好是一位男同学和一位女同学的概率为:= ,
故答案为
【分析】先利用树状图求出所有等可能的情况数,再利用概率公式求解即可。
13.【答案】1或2
【解析】【解答】解:函数y= 的图象如图:
根据图象知道当y=1或2时,对应成立的x值恰好有三个,
∴k=1或2.
故答案为1或2.
【分析】首先在坐标系中画出已知函数y= 的图像,利用数形结合的方法即可找到Y=K 成立的X值恰好有三个的k值。
14.【答案】﹣1≤t<8
【解析】【解答】解:对称轴为直线x=﹣ =1,
解得b=﹣2,
∴二次函数解析式为y=x2﹣2x,即y=(x﹣1)2﹣1,
x=﹣1时,y=1+2=3,
x=4时,y=16﹣2×4=8,
y=(x﹣1)2﹣1的最小值是﹣1,
∵x2+bx﹣t=0相当于y=x2+bx与直线y=t的交点的横坐标,如下图所示
∴当﹣1≤t<8时,在﹣1<x<4的范围内有解.
故答案为:﹣1≤t<8.
【分析】根据对称轴求出b的值,从而得到x=﹣1、4时的函数值,再根据一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解相当于y=x2+bx与y=t在x的范围内有交点解答.
15.【答案】
【解析】【解答】如下图,过点B作CE的垂线,交CE延长线于点F,AD与CE交于点H.
∵AD⊥EC,AD是∠EAC的角平分线
∴∠EAH=∠HAC
∴∠AEH=∠ACH,∴AE=AC,△AEC是等腰三角形
∵CE=4
∴EH=HC=2
∵CE是△ABC的中线,∴AE=EB
∵∠AEH=∠FEB,∠AHE=∠BFE=90°
∴△AEH≌△BEF
∴EF=2,FC=2+2+2=6,BF=AH
∵∠DCH=∠BCF,∠DHC=∠BFC=90°
∴△DCH∽△BCF
∴
∴3DH=BF,∴3DH=HA
∵AD=4
∴HD=1,FB=3
∴在Rt△CBF中,CB=
故答案为:
【分析】如下图,过点B作CE的垂线,交CE延长线于点F,先证△BFE≌△AHE,然后利用AD⊥CE可得FE、EH、HC的长,接着证△BFE∽△DHC,利用线段比的关系可求得BC的长.
16.【答案】(1)
(2)-3
(3)
【解析】【解答】解:(1)对于二次函数 ,
对称轴为 ,
当 时,二次函数的对称轴为 ;
故答案为: ;
(2)∵反比例函数 的图象过点P(2,y1),
∴ ,
故答案为: ;
(3)同(2)求得点P(2, ),Q(6, ),
如图,当二次函数的对称轴在P、Q两点之间时,二次函数的图象与PQ才有两个公共点,
∴ ,
当 时, ,
解方程: ,得 (舍去),
当 时, ,
解方程: ,得 (舍去),
则k的取值范围是 .
故答案为: .
【分析】(1)二次函数的对称轴为 ,代入数据即可求解;
(2)把点P(2,y1)代入 即可求解;
(3)根据题意知二次函数的对称轴在P、Q两点之间时,二次函数的图象与PQ才有两个公共点,当 或 时,二次函数的值应该小于或等于反比例函数的值,二次函数的图象与PQ才有两个公共点,据此求解即可.
17.【答案】(1)解:如图,即为所求作;
(2)
【解析】【解答】解:(2)如图,,
∴点A在旋转过程中经过的路线长为,
故答案为:.
【分析】(1)利用方格纸的特点及旋转的性质,结合旋转的方向和角度,分别作出但A、B绕点O顺时针旋转90°后的对应点A1、B1,再顺次连接A1、B1、O即可;
(2)利用勾股定理算出OA的长,进而根据弧长计算公式“”计算即可.
18.【答案】解:S阴=S正-S扇+S扇-S△+S△-S小扇
S阴=S正-S小扇
S阴=22-
答:阴影部分的面积是2.43平方厘米。
【解析】【分析】三角形CDE和三角形BAF是完全一样的等腰直角三角形,阴影部分的面积=正方形的面积-最右边扇形的面积;其中,正方形的面积=边长×边长,扇形的面积=π×半径2×45° ÷360°。
19.【答案】(1)证明:已知 ,
∴ 为直径,
∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴四边形 为平行四边形,
又∵ ,
∴四边形 是菱形;
(2)解:∵ , ,
∴ ,
∵四边形 内接于 ,
∴
∵ 四边形 是菱形,
∴ , ,
∵ ,
在 中,设 ,则 ,
∴ , ,
∵ ,
∴ ,
解得 或 (舍去),
∴ ,
∴在 中,
有 .
即 的直径长为 .
【解析】【分析】(1)由题意用角边角可证△DEG≌△FCG,则ED=FC,由一组对边平行且相等的四边形是平行四边形可得四边形DCFE为平行四边形,再根据对角线互相垂直的平行四边形是菱形可求解;
(2)在Rt△BED中,由已知的等式设DE=3a,则BE=4a,在Rt△ABC中用勾股定理可得关于a的方程,解方程即求得a的值;在Rt△ACD中用勾股定理求得AD的值即可.
20.【答案】解:(1)出现向上点数为6的频率=;
(2)丙的说法不正确,
理由:(1)因为实验次数较多时,向上点数为6的频率接近于概率,但不说明概率就等一定等于频率;
(2)从概率角度来说,向上点数为6的概率是的意义是指平均每6次出现1次;
(3)用表格列出所有等可能性结果:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
共有36种等可能性结果,其中点数之和为3的倍数可能性结果有12个
∴P(点数之和为3的倍数)==.
【解析】【分析】(1)直接利用概率公式求得概率即可;
(2)利用概率的意义分别分析后即可判断谁的说法正确;
(3)列表将所有等可能的结果列举出来,利用概率公式求解即可.
21.【答案】(1)
(2)解:连接OC、OD,
∵直径AB=4,CD=2,
∴OC=OD=CD=2,
∴△OCD是等边三角形,
∴∠COD=60°,
∴∠DAC=∠COD=30°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠E=90°-∠DAC=60°;
(3)解:如图,连接OC、OD、BD,
∵直径AB=4,CD=2,
∴OC=OD=CD=2,
∴△OCD是等边三角形,
∴∠COD=60°,
∴∠DBC=∠COD=30°,
∵AB是圆O的直径,
∴∠ADB=90°,
∴∠E=90°-∠DBC=60°.
【解析】【解答】解:(1)如图,连接OC、OD、BD,
∵直径AB=4,CD=2,
∴OC=OD=CD=2,
∴△OCD是等边三角形,
∴∠COD=60°,
∴∠DBC=∠COD=30°,
∵AB是圆O的直径,
∴∠ADB=90°=∠BDE,
∴∠E=90°-∠DBC=60°;
故答案为:60°;
【分析】(1)连接OC、OD、BD,由三边相等的三角形是等边三角形可得△OCD是等边三角形,由等边三角形的性质及同弧所对的圆周角等于圆心角的一半得∠DBC=∠COD=30°,由直径所对的圆周角是直角得∠ADB=90°=∠BDE,最后根据直角三角形的两锐角互余可算出∠E的度数;
(2)连接OC、OD,由三边相等的三角形是等边三角形可得△OCD是等边三角形,由等边三角形的性质及同弧所对的圆周角等于圆心角的一半得∠DAC=∠COD=30°,由直径所对的圆周角是直角得∠ACB=90°,最后根据直角三角形的两锐角互余可算出∠E的度数;
(3)连接OC、OD、BD,由三边相等的三角形是等边三角形可得△OCD是等边三角形,由等边三角形的性质及同弧所对的圆周角等于圆心角的一半得∠DBC=∠COD=30°,由直径所对的圆周角是直角得∠ADB=90°,最后根据直角三角形的两锐角互余可算出∠BED的度数,最后根据对顶角相等得出答案.
22.【答案】(1)证明:是正方形的对角线,
,,,
,
≌,
,
,
,
;
(2)解:,且,
,
由知,,
,
四边形是正方形,
,,,
,
,
,
≌,
,
,
,
,
,
设正方形的边长为,
,
,
在中,,
,
或舍去,
正方形的边长为;
(3)解:如图,过点作交于点,
由知,≌,
,,
,,
,
,
,
,
,,,
,
,
,
,
,,
,,
,
,
∽,
,
.
【解析】【分析】(1)通过边角边证明≌,得到,再利用两平行直线之间内错角相等得到,进而得到;
(2)根据等边对等角和三角形外角性质得,进而推得,再利用勾股定理和含角的性质求正方形的边长;
(3)过点作交于点,结合(1)知≌,利用等角对等边证明,,根据得到,由得到∽,进而求 的值.
23.【答案】(1)垂直且相等
(2)解:,,
∽,
,
线段EH绕点E逆时针旋转得到线段EG,
,
,
,
;
(3)证明:如图,
延长MB至X,连接AX,使BX=BM,作∠AMR=∠H,交AX于R,
,
,
,
,,
设∠XAB=∠BAM=,
,,
,
,
,
,
,,,
≌,
【解析】【解答】解:(1)∵四边形ABCD是正方形,
∴∠BAD=∠ADN=∠ADC=∠B=90°,AD=AB,
又∵BM=DN,
∴△ABM≌△ADN(SAS),
∴AM=AN,∠BAM=∠DAN,
∴∠MAN=∠DAN+∠MAD=∠BAM+∠MAD=∠BAD=90°,
∴AM⊥AN,
故答案为:垂直且相等;
【分析】(1)由正方形性质得∠BAD=∠ADN=∠ADC=∠B=90°,AD=AB,结合已知,由SAS判断出△ABM≌△ADN,由全等三角形的性质得AM=AN,∠BAM=∠DAN,进而根据角的和差及等量代换可得∠MAN=90°,从而可得结论;
(2)首先由有两组角对应相等的两个三角形相似得△HEF∽△HAM,由相似三角形的对应边成比例建立方程可求出AH的长;
(3)延长MB至X,连接AX,使BX=BM,作∠AMR=∠H,交AX于R,由线段垂直平分线的性质得AX=AM,由等腰三角形性质得∠XAB=∠BAM,∠X=∠AMB,设∠XAB=∠BAM=,根据已知、三角形的内角和定理、三角形外角和定理推出∠X=∠MRX,由等角对等边得RM=XM,然后用ASA判断出△HEF≌△MAR,由全等三角形的对应边相等可得结论.
24.【答案】(1)解:∵A(0,3),B(-1,0),
∴OA=3,OB=1,
根据旋转的性质得OC=OA=3,
∴C(3,0),
把A(0,3),B(-1,0),C(3,0),分别代入y=ax2+bx+c得
,
解得,
∴二次函数的解析式为:y=-x2+2x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点P的坐标为(1,4);
(2)解:①设,
直线:过定点,抛物线的顶点坐标为,
,
,
,
联立
得,
,
,
;
②证明:过点作轴,垂足为,分别过点,作的垂线,垂足分别为、,
设.
,在二次函数图象上,
,.
,
,,,,
,
,
由①可知,
,
,
,
,
,
,
,即,
无论为何值,恒为直角三角形;
③
【解析】【解答】解:(2)③∵恒为直角三角形,,
∴外接圆圆心是线段的中点;
设线段的中点,
∵,,.
∴
∴的中点为,
,
化简,得,
抛物线的表达式为.
【分析】(1)根据点A、B的坐标可得OA、OB的长,根据旋转的性质可得OC=OA,从而得出点C的坐标,然后利用待定系数法求抛物线的解析式,再将解析式配成顶点式可得点点P的坐标;
(2)①设M(x1,y1),N(x2,y2),易得定点Q为(1,3),则PQ=1,根据三角形面积公式得x2-x1=4,联立抛物线与直线的解析式得x2+(k-2)x-k=0,由根与系数的关系得x1+x2=2-k,x2x1=-k,再利用完全平方公式的恒等变形可得关于字母k的方程,求解即可;
② 过P作PG⊥x轴于G,过M,N作PG的垂线,垂足分别为E、F, 设M(x1,y1),N(x2,y2),根据两点间的距离公式表示出PE、ME、PF、NF,由正切函数的定义得tan∠PME=1-x1, , 然后根据根与系数的关系及等角的同名三角函数值相等证明∠PME=∠FPN,据此即可证得结论;
③根据圆周角定理得Rt△PMN外接圆的圆心是线段MN的中点;根据中点坐标公式计算即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
