二元一次不等式(组)表示的平面区域(辽宁省大连市中山区)
文档属性
| 名称 | 二元一次不等式(组)表示的平面区域(辽宁省大连市中山区) |

|
|
| 格式 | rar | ||
| 文件大小 | 136.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-25 00:00:00 | ||
图片预览




文档简介
课件11张PPT。二元一次不等式(组)
所表示的平面区域 1.二元一次不等式和二元一次不等式组的定义 :(1)二元一次不等式:含有两个未知数,并且未知数的最高次数是1的不等式叫做二元一次不等式。
(2)二元一次不等式组:有几个二元一次不等式组成的不等式组称为二元一次不等式组。
(3)二元一次不等式(组)的解集:满足二元一次不等式(组)的x和y的取值构成有序实数对(x,y),所有这样的有序实数对(x,y)构成的集合称为二元一次不等式(组)的解集。2.二元一次不等式 的形式:Ax+By+C>0
或Ax+By+C<0 (2)探究先研究具体的二元一次不等式x-y<6的解集所表示的图形
在平面直角坐标系内,x-y=6表示一条直线。平面内所有的点被直线分成三类:第一类:在直线x-y=6上的点;
第二类:在直线x-y=6左上方的区域内的点;
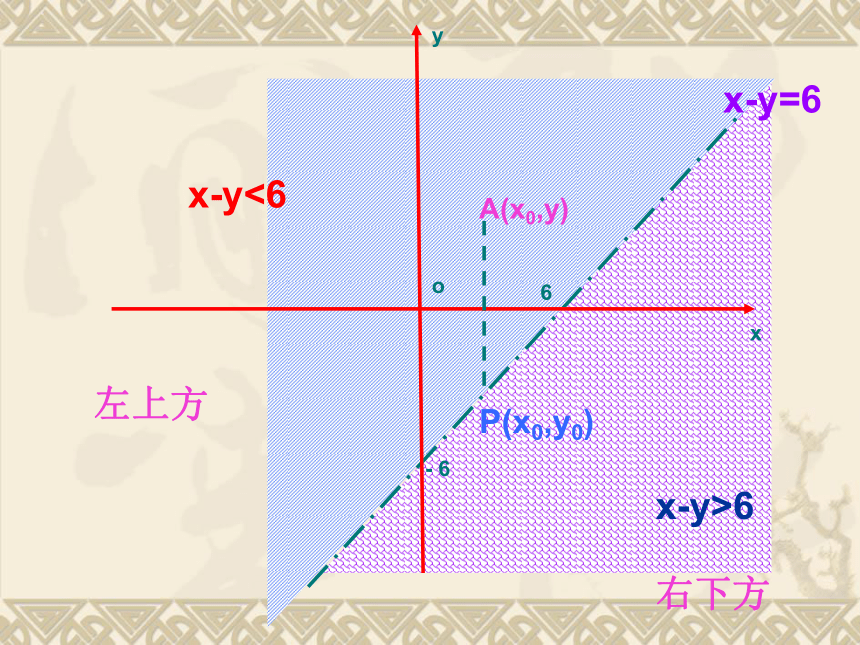
第三类:在直线x-y=6右下方的区域内的点。x-y=6x-y<6x-y>6左上方右下方A(x0,y)P(x0,y0)在平面直角坐标系中,
不等式x-y<6表示直线x-y=6左上方的平面区域;如图。
类似的:二元一次不等式x-y>6表示直线
x-y=6右下方的区域;如图。
直线叫做这两个区域的边界
3)结论:二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)4).二元一次不等式表示哪个平面区域的判断方法: (1)画直线Ax+By+C=0
(2)在直线Ax+By+C=0某一侧任取一特殊点,
把它的坐标代入Ax+By+C,所得到实数的符号,可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点)直线定界,特殊点定域 例1 画出 不等式表示的平面区域。解:先画直线(画成虚线) 取原点(0,0),代入 x+4y-4 ∵0+4×0-4=-4<0,∴原点在 表示的平面区域内, 不等式表示的区域如图: 例2 用平面区域表示.不等式组的解集。变式1、画出不等式表示的平面区域。变式2、由直线,和围成的三角形区域(包括边界)用不等
式可表示为 。
所表示的平面区域 1.二元一次不等式和二元一次不等式组的定义 :(1)二元一次不等式:含有两个未知数,并且未知数的最高次数是1的不等式叫做二元一次不等式。
(2)二元一次不等式组:有几个二元一次不等式组成的不等式组称为二元一次不等式组。
(3)二元一次不等式(组)的解集:满足二元一次不等式(组)的x和y的取值构成有序实数对(x,y),所有这样的有序实数对(x,y)构成的集合称为二元一次不等式(组)的解集。2.二元一次不等式 的形式:Ax+By+C>0
或Ax+By+C<0 (2)探究先研究具体的二元一次不等式x-y<6的解集所表示的图形
在平面直角坐标系内,x-y=6表示一条直线。平面内所有的点被直线分成三类:第一类:在直线x-y=6上的点;
第二类:在直线x-y=6左上方的区域内的点;
第三类:在直线x-y=6右下方的区域内的点。x-y=6x-y<6x-y>6左上方右下方A(x0,y)P(x0,y0)在平面直角坐标系中,
不等式x-y<6表示直线x-y=6左上方的平面区域;如图。
类似的:二元一次不等式x-y>6表示直线
x-y=6右下方的区域;如图。
直线叫做这两个区域的边界
3)结论:二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)4).二元一次不等式表示哪个平面区域的判断方法: (1)画直线Ax+By+C=0
(2)在直线Ax+By+C=0某一侧任取一特殊点,
把它的坐标代入Ax+By+C,所得到实数的符号,可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点)直线定界,特殊点定域 例1 画出 不等式表示的平面区域。解:先画直线(画成虚线) 取原点(0,0),代入 x+4y-4 ∵0+4×0-4=-4<0,∴原点在 表示的平面区域内, 不等式表示的区域如图: 例2 用平面区域表示.不等式组的解集。变式1、画出不等式表示的平面区域。变式2、由直线,和围成的三角形区域(包括边界)用不等
式可表示为 。
