高一数学必修一5.7《三角函数的应用》课时练习(含答案)
文档属性
| 名称 | 高一数学必修一5.7《三角函数的应用》课时练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览



文档简介
高一数学必修一5.7《三角函数的应用》课时练习
三角函数与几何
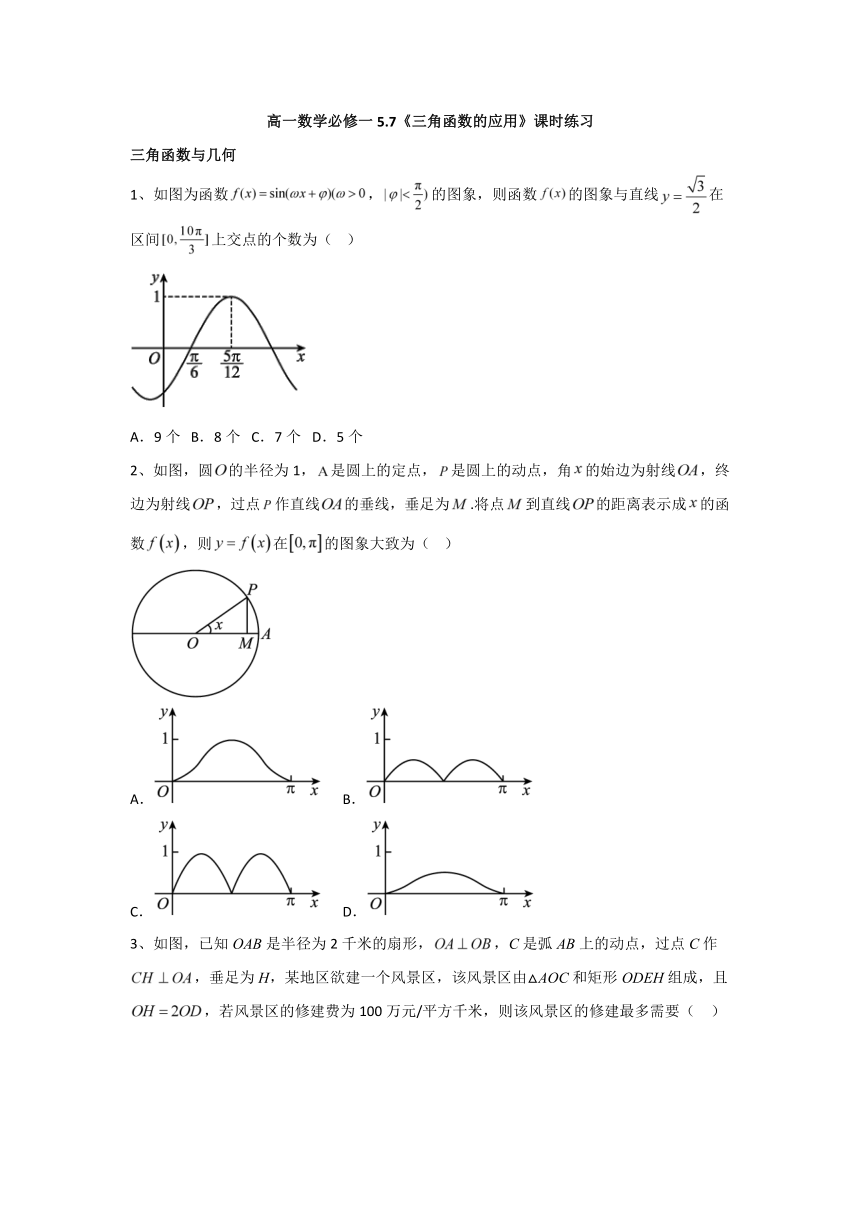
1、如图为函数,的图象,则函数的图象与直线在区间上交点的个数为( )
A.9个 B.8个 C.7个 D.5个
2、如图,圆的半径为1,是圆上的定点,是圆上的动点,角的始边为射线,终边为射线,过点作直线的垂线,垂足为.将点到直线的距离表示成的函数,则在的图象大致为( )
A. B.
C. D.
3、如图,已知OAB是半径为2千米的扇形,,C是弧AB上的动点,过点C作,垂足为H,某地区欲建一个风景区,该风景区由△AOC和矩形ODEH组成,且,若风景区的修建费为100万元/平方千米,则该风景区的修建最多需要( )
A.260万元 B.265万元 C.255万元 D.250万元
4、我国古代数学家赵爽在注解《周髀算经》一书时介绍了“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的大正方形如图所示,记直角三角形较小的锐角为,大正方形的面积为,小正方形的面积为,若,则的值为( )
A. B. C. D.
5、已知正方形边长为两点分别为边上动点,,则的周长为 .
6、在校园美化、改造活动中,要在半径为、圆心角为的扇形空地的内部修建一矩形观赛场地,如图所示.取的中点M,记.
(1)写出矩形的面积S与角的函数关系式;
(2)求当角为何值时,矩形的面积最大?并求出最大面积.
三角函数与物理
7、声音是由物体的振动产生的声波,一个声音可以是纯音或复合音,复合音由纯音合成,纯音的函数解析式为.设声音的函数为,音的响度与的最大值有关,最大值越大,响度越大;音调与的最小正周期有关,最小正周期越大声音越低沉.假设复合音甲的函数解析式是,纯音乙的函数解析式是,则下列说法正确的有( )
A.纯音乙的响度与ω无关
B.纯音乙的音调与ω无关
C.若复合音甲的音调比纯音乙的音调低沉,则ω<1
D.复合音甲的响度与纯音乙的响度一样大
8、如图,一台发电机产生的电流是正弦式电流,即电压U(单位:V)和时间t(单位:s)满足.在一个周期内,电压的绝对值超过的时间为( ).
s B. 1S C. S D. S
9、如图,弹簧挂着的小球做上下振动,它在t秒时相对于平衡位置(即静止时的位置)的高度h厘米满足下列关系:,,则每秒钟小球能振动( ).
次 B. 次 C. 次 D. 次
10、如图,是一种碳原子簇,它是由60个碳原子构成的,其结构是以正五边形和正六边形面组成的凸32面体,这60个原子在空间进行排列时,形成一个化学键最稳定的空间排列位置,恰好与足球表面格的排列一致,因此也叫足球烯.根据杂化轨道的正交归一条件,两个等性杂化轨道的最大值之间的夹角满足:,式中分别为杂化轨道中轨道所占的百分数.中的杂化轨道为等性杂化轨道,且无轨道参与杂化,碳原子杂化轨道理论计算值为,它表示参与杂化的轨道数之比为,由此可计算得一个中的凸32面体结构中两个等性杂化轨道的最大值之间的夹角的余弦值为( )
A. B. C. D.
11、如图,一根绝对刚性且长度不变 质量可忽略不计的线,一端固定,另一端悬挂一个沙漏.让沙漏在偏离平衡位置一定角度(最大偏角)后在重力作用下在铅垂面内做周期摆动,沙漏摆动时离开平衡位置的位移(单位:)与时间t(单位:s)满足函数关系,若函数在区间上的最大值为,最小值为,则的最小值为 .
三角函数与生活
12、记某时钟的中心点为,分针针尖对应的端点为.已知分针长,且分针从12点位置开始绕中心点顺时针匀速转动.若以中心点为原点,3点和12点方向分别为轴和轴正方向建立平面直角坐标系,则点到轴的距离(单位:)与时间t(单位:min)的函数解析式为( )
A. B.
C. D.
13、水车是古老黄河的文化符号,是我国劳动人民智慧的结晶,是最早的自动灌溉系统.黄河边上的一架水车直径为16米,入水深度4米,为了计算水车的旋转速度,某人给刚出水面的一个水斗(图中点A)做上记号,经过60秒该水斗到达水车最顶端(图中点B),再经过11分20秒,做记号的水斗与水面的距离为n米,则n所在的范围是( )
A. B. C. D.
14、健康成年人的收缩压和舒张压一般为90~139mmhg和60~89mmhg,心脏跳动时,血压在增加或减小,血压的最大值、最小值分别为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数为120/80mmhg为标准值.设某人的血压满足函数式,其中为血压(mmhg),t为时间(min).给出以下结论:
①此人的血压在血压计上的读数为140/90mmhg ②此人的血压在健康范围内
③此人的血压已超过标准值 ④此人的心跳为80次/分
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
15、如图,水利灌溉工具筒车的转轮中心到水面的距离为,筒车的半径是,盛水筒的初始位置为与水平正方向的夹角为.若筒车以角速度沿逆时针方向转动,t为筒车转动后盛水筒第一次到达入水点所需的时间(单位:),则( )
A. B. C. D.
16、如图,某公园有一块扇形人工湖OAB,其中,千米,为了增加人工湖的观赏性,政府计划在人工湖上建造两个观景区,其中荷花池观景区的形状为矩形,喷泉观景区的形状为,且C在OB上,D在OA上,P在上,记.
(1)试用θ分别表示矩形和的面积;
(2)若在PD的位置架起一座观景桥,已知建造观景桥的费用为每千米8万元(包含桥的宽度费用),建造喷泉观景区的费用为每平方千米16万元,建造荷花池的总费用为6万元.求当θ为多少时,建造该观景区总费用最低,并求出其最低费用.
17、我国核电建设占全球在建核电机组的40%以上,是全球核电在建规模最大的国家.核电抗飞防爆结构是保障核电工程安全的重要基础设施,为此国家制定了一系列核电钢筋混凝土施工强制规范,连接技术全面采用HRB500高强钢筋替代HRB400及以下钢筋.某项目课题组针对HRB500高强钢筋的现场加工难题,对螺纹滚道几何成形机理进行了深入研究,研究中发现某S型螺纹丝杠旋铣的滚道径向残留高度y(单位:mm)关于滚道径向方位角x(单位:rad)的函数近似地满足,其图象的一部分如图所示.
(1)求函数的解析式;
(2)为制造一批特殊钢筋混凝土,现需一批滚道径向残留高度不低于0.015mm且不高于0.02mm的钢筋,若这批钢筋由题中这种S型螺纹丝杠旋铣制作,求这种S型螺纹丝杠旋铣能制作出符合要求的钢筋的比例.
参考答案:
1、C 2、 B 3、D 4、A 5、4
6、 (1)S,.
(2)故当时,矩形的面积最大,最大值为.
7、A 8、A 9、C 10、C
11、
12、 D 13、B 14、 C 15、C
16、(1)矩形的面积为;
的面积为:
(2),万元
17、(1)
(2)
三角函数与几何
1、如图为函数,的图象,则函数的图象与直线在区间上交点的个数为( )
A.9个 B.8个 C.7个 D.5个
2、如图,圆的半径为1,是圆上的定点,是圆上的动点,角的始边为射线,终边为射线,过点作直线的垂线,垂足为.将点到直线的距离表示成的函数,则在的图象大致为( )
A. B.
C. D.
3、如图,已知OAB是半径为2千米的扇形,,C是弧AB上的动点,过点C作,垂足为H,某地区欲建一个风景区,该风景区由△AOC和矩形ODEH组成,且,若风景区的修建费为100万元/平方千米,则该风景区的修建最多需要( )
A.260万元 B.265万元 C.255万元 D.250万元
4、我国古代数学家赵爽在注解《周髀算经》一书时介绍了“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的大正方形如图所示,记直角三角形较小的锐角为,大正方形的面积为,小正方形的面积为,若,则的值为( )
A. B. C. D.
5、已知正方形边长为两点分别为边上动点,,则的周长为 .
6、在校园美化、改造活动中,要在半径为、圆心角为的扇形空地的内部修建一矩形观赛场地,如图所示.取的中点M,记.
(1)写出矩形的面积S与角的函数关系式;
(2)求当角为何值时,矩形的面积最大?并求出最大面积.
三角函数与物理
7、声音是由物体的振动产生的声波,一个声音可以是纯音或复合音,复合音由纯音合成,纯音的函数解析式为.设声音的函数为,音的响度与的最大值有关,最大值越大,响度越大;音调与的最小正周期有关,最小正周期越大声音越低沉.假设复合音甲的函数解析式是,纯音乙的函数解析式是,则下列说法正确的有( )
A.纯音乙的响度与ω无关
B.纯音乙的音调与ω无关
C.若复合音甲的音调比纯音乙的音调低沉,则ω<1
D.复合音甲的响度与纯音乙的响度一样大
8、如图,一台发电机产生的电流是正弦式电流,即电压U(单位:V)和时间t(单位:s)满足.在一个周期内,电压的绝对值超过的时间为( ).
s B. 1S C. S D. S
9、如图,弹簧挂着的小球做上下振动,它在t秒时相对于平衡位置(即静止时的位置)的高度h厘米满足下列关系:,,则每秒钟小球能振动( ).
次 B. 次 C. 次 D. 次
10、如图,是一种碳原子簇,它是由60个碳原子构成的,其结构是以正五边形和正六边形面组成的凸32面体,这60个原子在空间进行排列时,形成一个化学键最稳定的空间排列位置,恰好与足球表面格的排列一致,因此也叫足球烯.根据杂化轨道的正交归一条件,两个等性杂化轨道的最大值之间的夹角满足:,式中分别为杂化轨道中轨道所占的百分数.中的杂化轨道为等性杂化轨道,且无轨道参与杂化,碳原子杂化轨道理论计算值为,它表示参与杂化的轨道数之比为,由此可计算得一个中的凸32面体结构中两个等性杂化轨道的最大值之间的夹角的余弦值为( )
A. B. C. D.
11、如图,一根绝对刚性且长度不变 质量可忽略不计的线,一端固定,另一端悬挂一个沙漏.让沙漏在偏离平衡位置一定角度(最大偏角)后在重力作用下在铅垂面内做周期摆动,沙漏摆动时离开平衡位置的位移(单位:)与时间t(单位:s)满足函数关系,若函数在区间上的最大值为,最小值为,则的最小值为 .
三角函数与生活
12、记某时钟的中心点为,分针针尖对应的端点为.已知分针长,且分针从12点位置开始绕中心点顺时针匀速转动.若以中心点为原点,3点和12点方向分别为轴和轴正方向建立平面直角坐标系,则点到轴的距离(单位:)与时间t(单位:min)的函数解析式为( )
A. B.
C. D.
13、水车是古老黄河的文化符号,是我国劳动人民智慧的结晶,是最早的自动灌溉系统.黄河边上的一架水车直径为16米,入水深度4米,为了计算水车的旋转速度,某人给刚出水面的一个水斗(图中点A)做上记号,经过60秒该水斗到达水车最顶端(图中点B),再经过11分20秒,做记号的水斗与水面的距离为n米,则n所在的范围是( )
A. B. C. D.
14、健康成年人的收缩压和舒张压一般为90~139mmhg和60~89mmhg,心脏跳动时,血压在增加或减小,血压的最大值、最小值分别为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数为120/80mmhg为标准值.设某人的血压满足函数式,其中为血压(mmhg),t为时间(min).给出以下结论:
①此人的血压在血压计上的读数为140/90mmhg ②此人的血压在健康范围内
③此人的血压已超过标准值 ④此人的心跳为80次/分
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
15、如图,水利灌溉工具筒车的转轮中心到水面的距离为,筒车的半径是,盛水筒的初始位置为与水平正方向的夹角为.若筒车以角速度沿逆时针方向转动,t为筒车转动后盛水筒第一次到达入水点所需的时间(单位:),则( )
A. B. C. D.
16、如图,某公园有一块扇形人工湖OAB,其中,千米,为了增加人工湖的观赏性,政府计划在人工湖上建造两个观景区,其中荷花池观景区的形状为矩形,喷泉观景区的形状为,且C在OB上,D在OA上,P在上,记.
(1)试用θ分别表示矩形和的面积;
(2)若在PD的位置架起一座观景桥,已知建造观景桥的费用为每千米8万元(包含桥的宽度费用),建造喷泉观景区的费用为每平方千米16万元,建造荷花池的总费用为6万元.求当θ为多少时,建造该观景区总费用最低,并求出其最低费用.
17、我国核电建设占全球在建核电机组的40%以上,是全球核电在建规模最大的国家.核电抗飞防爆结构是保障核电工程安全的重要基础设施,为此国家制定了一系列核电钢筋混凝土施工强制规范,连接技术全面采用HRB500高强钢筋替代HRB400及以下钢筋.某项目课题组针对HRB500高强钢筋的现场加工难题,对螺纹滚道几何成形机理进行了深入研究,研究中发现某S型螺纹丝杠旋铣的滚道径向残留高度y(单位:mm)关于滚道径向方位角x(单位:rad)的函数近似地满足,其图象的一部分如图所示.
(1)求函数的解析式;
(2)为制造一批特殊钢筋混凝土,现需一批滚道径向残留高度不低于0.015mm且不高于0.02mm的钢筋,若这批钢筋由题中这种S型螺纹丝杠旋铣制作,求这种S型螺纹丝杠旋铣能制作出符合要求的钢筋的比例.
参考答案:
1、C 2、 B 3、D 4、A 5、4
6、 (1)S,.
(2)故当时,矩形的面积最大,最大值为.
7、A 8、A 9、C 10、C
11、
12、 D 13、B 14、 C 15、C
16、(1)矩形的面积为;
的面积为:
(2),万元
17、(1)
(2)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
