2024届广东省高三第一次学业水平考试(小高考)数学预测卷(PDF版含解析)
文档属性
| 名称 | 2024届广东省高三第一次学业水平考试(小高考)数学预测卷(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 19:57:00 | ||
图片预览




文档简介
2024届广东省第一次学业水平考试(小高考)数学预测卷
考试时间:90分钟,总分:150分,
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第 I卷(选择题)
一、选择题:本大题共 12小题,每小题 6分,共 72分.在每小题给出的四个
选项中,只有一项是符合题目要求的.
1. 已知直线 a、b 与平面 、 ,下列命题正确的是( )
A.若 // , ,则 // B.若 // , ,则 //
C.若 ⊥ , ,则 ⊥ D.若 ⊥ , ,则 ⊥
2 = + 2, ≤ 1. 已知函数 2 3, > 1,则 1 =( )
A.1 B.3 C.-3 D.-1
3. 将一颗骰子连续抛掷两次,至少出现一次 6点向上的概率是( )
A 1 11 25 1. B. C. D.
18 36 36 36
4. 设集合 = ∣1 ≤ ≤ 3 , = { ∣2 < < 4},则 ∩ =( )
A.{ ∣1 ≤ < 4} B.{ ∣1 < < 4}
C.{ ∣2 < ≤ 3} D. ∣2 ≤ ≤ 3
5. 下列函数在定义域内为偶函数的是( )
A = 1. B. = 3 C. = 2 D. = 1
6. 已知 > 0,则 + 1( )
A.有最大值 1 B.有最小值 1
C.有最大值 2 D.有最小值 2
7. 不等式 2 2 3 > 0的解集是( )
A.{ ∣ < 1.5或 > 2} B. C.{ ∣1.5 < < 2} D.
第 1页,共 4页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
8. 指数函数 = 与 = 的图象如图所示,则( )
A. > 1,0 < < 1 B. > 1, > 1
C.0 < < 1, > 1 D.0 < < 1,0 < < 1
9. 已知角 的顶点与原点重合,始边与 轴的正半轴重合,点 (1, 3) 在
角 的终边上,则 sin = ( )
A 10 B 10 C 3 10 D 3 10. . . .
10 10 10 10
10. 某饮料生产企业推出了一种有一定几率中奖的新饮料.甲 乙两名同学
都购买了这种饮料,设事件 为“甲 乙都中奖”,则与 互为对立事件的是( )
A.甲 乙恰有一人中奖 B.甲 乙都没中奖
C.甲 乙至少有一人中奖 D.甲 乙至多有一人中奖
11 = sin + π π. 将函数 的图象向右平移 个单位长度后,所得图象对应的
3 6
函数为( )
A. = sin + π B π. = sin
6 6
C. = cos D. = cos
12. 在△ 中,点 为边 的中点,记� �� �� = � �, � �� � = � �,则 ��� �� =( )
A 1 � � + � � B 1. . � � � � C 1 � � + 1 � � D 1 � � 1. . � �
2 2 2 2 2 2
第 II卷(非选择题)
二、填空题:本大题共 6小题,每小题 6分,共 36分.
13. 请写出一个最小正周期为π的函数 .(写出一个即可)
14. 已知复数 = 2 3i(i是虚数单位),则它的模 =
15. 一个正方体的体对角线长为 2,它的顶点都在同一球面上,则该球的
体积为 .
试卷第 2页,共 4页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
16.已知向量� �, � �满足 � � = 2, � � = 1,� �, � �的夹角为 60°,则 2� � + � � = .
17. 某工厂生产甲、乙、丙三种不同型号的产品,产量分别为 200,350,450
件,为检验产品的质量,用分层抽样的方法从以上产品中抽取一个容量为
的样本,已知从乙产品中抽取了 7件,则 = .
3 2
18 + 2 +1. 已知 = 2 + 是奇函数,则 = . +1
三、解答题:本大题共 4 小题,第 19~21 题各 10 分,第 22 题
12 分,共 42 分.解答需写出文字说明、证明过程和演算步骤.
19 1.在△ 中,角 , , 所对的边分别为 , , ,且 = 4, = 5,cos = .
8
(1)求△ 的面积;(4分)
(2)求边长 及 sin 的值.(6分)
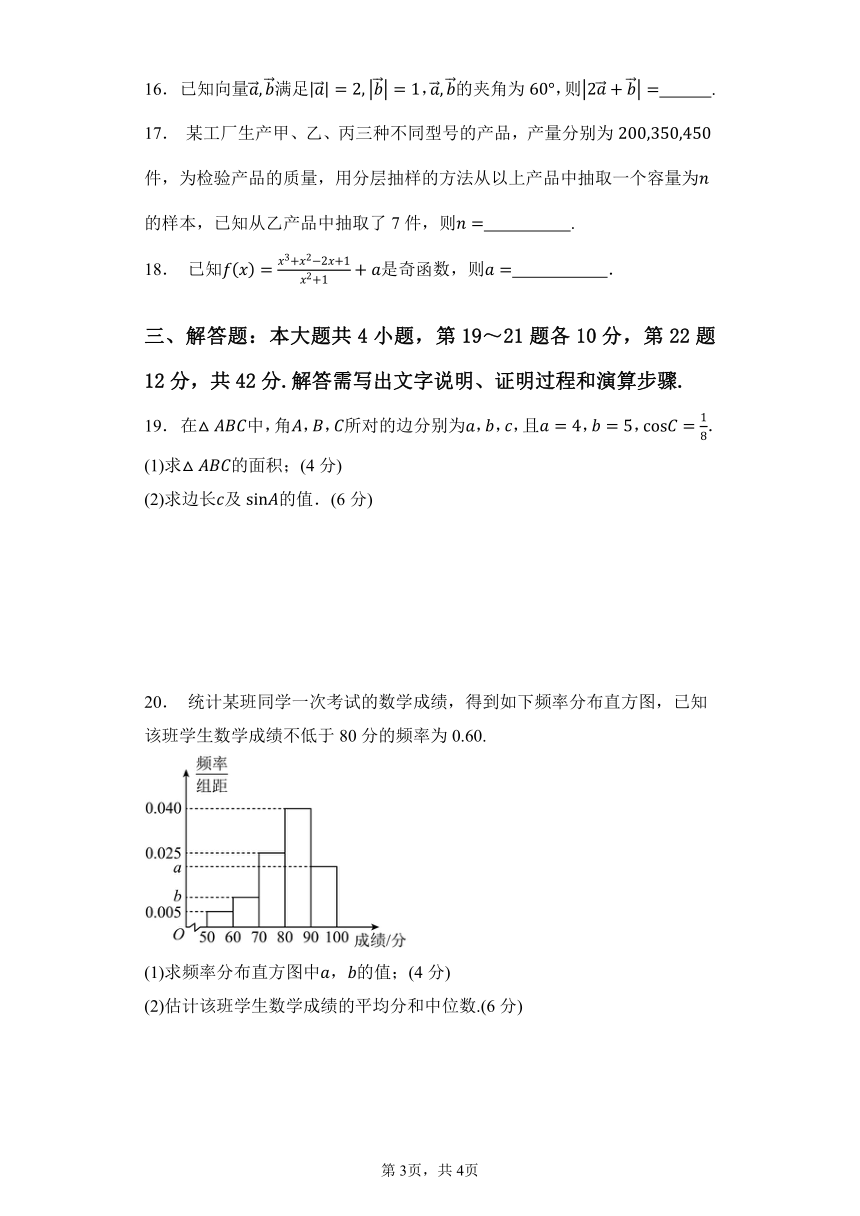
20. 统计某班同学一次考试的数学成绩,得到如下频率分布直方图,已知
该班学生数学成绩不低于 80分的频率为 0.60.
(1)求频率分布直方图中 , 的值;(4分)
(2)估计该班学生数学成绩的平均分和中位数.(6分)
第 3页,共 4页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
21. 某市为鼓励居民节约用电,采用阶梯电价的收费方式,当月用电量不
超过 100度的部分,按 0.4元/度收费;超过 100度的部分,按 0.8元/度收费.
(1)若某户居民用电量为 120度,则该月电费为多少元?(5分)
(2)若某户居民某月电费为 60元,则其用电量为多少度?(5分)
22. 如图,在正方体 1 1 1 1中, = 1.
(1)求证: //平面 1 1;(4分)
(2)求证: 1 ⊥平面 1 1;(4分)
(3)求直线 1 和平面 1 1所成的角.(4分)
试卷第 4页,共 4页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
参考答案:
1.C
【分析】由线面位置关系的判定,分析选项中结论是否正确.
【详解】A选项,缺条件 ,结论不成立;
B选项,直线 与直线 可能平行可能异面,结论不成立;
C选项,由直线与平面垂直的定义可知,结论正确
D选项,直线 可能与 平行,可能在 内,也可能与 相交,不一定满足垂直,结论不成立.
故选:C
2.B
【分析】计算出 1 = 3,从而求出 1 .
【详解】 1 = 1 + 2 = 3, 1 = 3 = 6 3 = 3.
故选:B
3.B
【分析】由题意确定出现一次 6点向上的概率,可得没有一次 6点向上的概率,利用对立事
件的概率关系求解即可.
1
【详解】将一颗质地均匀的骰子先后抛掷一次,出现一次 6点向上的概率为 ,
6
1 25
所以先后抛掷 2次,没有一次 6点向上的概率为(1 )2 = ,
6 36
25 11
所以至少出现一次 6点向上的概率为 1 = .
36 36
故选:B.
4.C
【分析】利用交集的定义求解.
【详解】集合 = ∣1 ≤ ≤ 3 , = { ∣2 < < 4},则 ∩ = { ∣2 < ≤ 3}.
故选:C.
5.C
【分析】利用函数的奇偶性定义判定即可.
1
【详解】对 A, = ≠ ,故 A不是偶函数;
对 B, = 3 = 3 ≠ ,故 B不是偶函数;
2
对 C, = 2的定义域为 R,关于原点对称,且 = = 2 = ,则其为偶函
数;
答案第 1页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
对 D, = 1 + ≠ ,故 D不是偶函数,
故选:C
6.D
【分析】由基本不等式求和的最小值.
1 1
【详解】已知 > 0,则 + ≥ 2 = 2,
1
当且仅当 = ,即 = 1 时等号成立,
则 + 1有最小值 2.
故选:D.
7.C
【分析】解一元二次不等式求得正确答案.
【详解】由 2 2 3 > 0 得 2 2 3 < 0,解得 1.5 < < 2,
所以原不等式的解集为{ ∣1.5 < < 2}.
故选:C
8.C
【分析】根据指数函数的性质即可得答案.
【详解】解:因为函数 = 的图象是下降的,所以 0 < < 1;
又因为函数 = 的图象是上升的,所以 > 1.
故选:C.
9.D
【分析】根据三角函数正弦定义相关知识可求.
【详解】因为角 的顶点与原点重合,始边与 轴的正半轴重合,点 (1, 3) 在角 的终边
上,
3 3 10
所以 sin = = ,
2 101 + 3 2
故选:D
10.D
【分析】根据互斥事件与对立事件的概念判断即可.
【详解】“甲、乙恰有一人中奖”与 互斥但不对立,故 A错误;
“甲、乙都没中奖”与 互斥但不对立,故 B错误;
答案第 2页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
“甲、乙至少有一人中奖”与 不互斥,故 C错误;
“甲、乙至多有一人中奖”与 互斥且对立,故 D正确.
故选:D.
11.A
【分析】根据三角函数图象平移变化可得.
π π
【详解】将函数 = sin + 的图象向右平移 个单位长度后,
3 6
π π π
所得图象对应的函数为 = sin + ,即 = sin + .
6 3 6
故选:A
12.C
【分析】利用平面向量的线性运算计算即可.
1 1 1
【详解】由题意可知 ��� �� = ��� �� = ��� �� � �� � = � � � � , ��� �� = ��� � + ��� �� = � �+ 1 � � � � =
2 2 2 2
1 � � + � � .
2
故选:C
13. = sin2 (答案不唯一)
【分析】根据三角函数周期公式确定 即可得答案.
【详解】由 = sin + 的周期为 = 2π = π,得 = 2,
不妨取 = 1, = 0,得一个满足题意的函数 = sin2 .
故答案为: = sin2 (答案不唯一)
14. 13
【分析】根据复数模的计算公式计算可得.
【详解】因为 = 2 3i,所以 = 22 + 3 2 = 13.
故答案为: 13
15 2π. / 2π
3 3
【分析】根据长方体外接球的特征即可求解半径,由体积公式即可求解.
【详解】根据长方体的结构特征可知长方体的体对角线为其外接球的一条直径 2 ,所以
3
2 = 2 = 2, 4 2故球的体积为 π × = 2π,
2 3 2 3
2π
故答案为:
3
答案第 3页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
16. 21
【分析】根据向量的模长公式直接代入求解即可.
2
【详解】 2� � + � � = 2� � + � � = 4� �2 + 4� � � � + � �2 = 4 × 4 + 4 × 2 × 1 × cos60° + 1 =
21,
故答案为: 21.
17.20
【分析】根据分层抽样的性质运算求解.
7
【详解】由题可知, = ,解得 = 20.
350 200+350+450
故答案为:20.
18. 1
【分析】根据奇函数定义求参数即可.
3+ 2 2 +1 3
【详解】因为 = 2 + =
2
2 + + 1, +1 +1
3
所以 = 2 + + 1,
2+1
则 + = 2 + 2,
因为 是奇函数,所以 + = 0,
所以 2 + 2 = 0,解得 = 1.
故答案为: 1
19.(1)15 7
4
(2) = 6 7,sin =
4
【分析】(1)利用平方关系和面积公式求解即可.
(2)利用余弦定理和正弦定理求解即可.
1
【详解】(1)由 cos = ,且 0 < < π,
8
3 7
则 sin = 1 cos2 = ,
8
1 15 7
所以 △ = sin = .2 4
(2)由 2 = 2 + 2 2 cos = 16 + 25 5 = 36,
则 = 6,
答案第 4页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
= sin = sin = 7又 ,则 .
sin sin 4
20.(1) = 0.02, = 0.01
(2)平均分、中位数分别为 81,82.5
【分析】(1)根据频率分布直方图的性质求解即可.
(2)利用平均数和中位数的定义和公式求解即可.
1 0.6【详解】( )由已知得 = 0.04 = 0.02,
10
则 0.005 + + 0.025 + 0.040 + 0.020 × 10 = 1,所以 = 0.01.
(2)该班学生数学成绩的平均分的估计值为:
55 × 0.005 + 65 × 0.01 + 75 × 0.025 + 85 × 0.04 + 95 × 0.02 × 10 = 81,
因为 0.005 + 0.01 + 0.025 × 10 = 0.4,
0.005 + 0.01 + 0.025 + 0.04 × 10 = 0.8,
所以中位数在 80,90 内.
0.5 0.4
故中位数为 80 + × 10 = 82.5.
0.4
21.(1)56
(2)125
【分析】(1)设用电量为 度,对应电费为 元,求出 关于 的分段函数,将 =120代入,
求解出该月电费;
(2)先判断出该户用电量超过了 100度,进而解方程,求出其用电量.
【详解】(1)设用电量为 度,对应电费为 元,
由题意得:当 ≤100时, =0.4 ;
当 >100时, =100×0.4+ 100 ×0.8=0.8 40,
即 = 0.4 , ≤1000.8 40, >100,
当 =120时, =0.8×120 40=56,
所以该月电费为 56元;
(2)因为 ≤100时, =0.4 ≤0.4×100=40<60,
所以该户用电量超过了 100度,
答案第 5页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
令 0.8 40=60,解得: =125,
故其用电量为 125度.
22.(1)证明见解析
(2)证明见解析
(3)30°
【分析】(1)由线面平行的判定可证明;
(2)先证明线线垂直,从而可得线面垂直;
(3)由(2)可得∠ 1 即为所求的角,再解三角形即可.
【详解】(1)证明:因为在正方体 1 1 1 1中,可知 // 1 1,而 平面 1 1,
1 1 平面 1 1,所以 //平面 1 1.
(2)证明:因为在正方体 1 1 1 1中,可知 1 1 ⊥平面 1 1 ,且 1 平面
1 1 ,所以 1 1 ⊥ 1,
又因为 1、 1 是正方形 1 1 的对角形,因此 1 ⊥ 1 ,
又 1 1 ∩ 1 = 1,且 1 1, 1 平面 1 1,
所以 1 ⊥平面 1 1.
(3)设 1与 1 的交点为 ,连接 1 ,由(2)可知直线 1 和平面 1 1所成的角为∠ 1 ,
且△ 1 为直角三角形,∠ 1 = 90°,
设正方体 1 1 1 1棱长为 2,可得 1 = 2 2, = 2,
所以∠ °1 = 30 ,因此直线 °1 和平面 1 1所成的角为30 .
答案第 6页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
考试时间:90分钟,总分:150分,
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第 I卷(选择题)
一、选择题:本大题共 12小题,每小题 6分,共 72分.在每小题给出的四个
选项中,只有一项是符合题目要求的.
1. 已知直线 a、b 与平面 、 ,下列命题正确的是( )
A.若 // , ,则 // B.若 // , ,则 //
C.若 ⊥ , ,则 ⊥ D.若 ⊥ , ,则 ⊥
2 = + 2, ≤ 1. 已知函数 2 3, > 1,则 1 =( )
A.1 B.3 C.-3 D.-1
3. 将一颗骰子连续抛掷两次,至少出现一次 6点向上的概率是( )
A 1 11 25 1. B. C. D.
18 36 36 36
4. 设集合 = ∣1 ≤ ≤ 3 , = { ∣2 < < 4},则 ∩ =( )
A.{ ∣1 ≤ < 4} B.{ ∣1 < < 4}
C.{ ∣2 < ≤ 3} D. ∣2 ≤ ≤ 3
5. 下列函数在定义域内为偶函数的是( )
A = 1. B. = 3 C. = 2 D. = 1
6. 已知 > 0,则 + 1( )
A.有最大值 1 B.有最小值 1
C.有最大值 2 D.有最小值 2
7. 不等式 2 2 3 > 0的解集是( )
A.{ ∣ < 1.5或 > 2} B. C.{ ∣1.5 < < 2} D.
第 1页,共 4页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
8. 指数函数 = 与 = 的图象如图所示,则( )
A. > 1,0 < < 1 B. > 1, > 1
C.0 < < 1, > 1 D.0 < < 1,0 < < 1
9. 已知角 的顶点与原点重合,始边与 轴的正半轴重合,点 (1, 3) 在
角 的终边上,则 sin = ( )
A 10 B 10 C 3 10 D 3 10. . . .
10 10 10 10
10. 某饮料生产企业推出了一种有一定几率中奖的新饮料.甲 乙两名同学
都购买了这种饮料,设事件 为“甲 乙都中奖”,则与 互为对立事件的是( )
A.甲 乙恰有一人中奖 B.甲 乙都没中奖
C.甲 乙至少有一人中奖 D.甲 乙至多有一人中奖
11 = sin + π π. 将函数 的图象向右平移 个单位长度后,所得图象对应的
3 6
函数为( )
A. = sin + π B π. = sin
6 6
C. = cos D. = cos
12. 在△ 中,点 为边 的中点,记� �� �� = � �, � �� � = � �,则 ��� �� =( )
A 1 � � + � � B 1. . � � � � C 1 � � + 1 � � D 1 � � 1. . � �
2 2 2 2 2 2
第 II卷(非选择题)
二、填空题:本大题共 6小题,每小题 6分,共 36分.
13. 请写出一个最小正周期为π的函数 .(写出一个即可)
14. 已知复数 = 2 3i(i是虚数单位),则它的模 =
15. 一个正方体的体对角线长为 2,它的顶点都在同一球面上,则该球的
体积为 .
试卷第 2页,共 4页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
16.已知向量� �, � �满足 � � = 2, � � = 1,� �, � �的夹角为 60°,则 2� � + � � = .
17. 某工厂生产甲、乙、丙三种不同型号的产品,产量分别为 200,350,450
件,为检验产品的质量,用分层抽样的方法从以上产品中抽取一个容量为
的样本,已知从乙产品中抽取了 7件,则 = .
3 2
18 + 2 +1. 已知 = 2 + 是奇函数,则 = . +1
三、解答题:本大题共 4 小题,第 19~21 题各 10 分,第 22 题
12 分,共 42 分.解答需写出文字说明、证明过程和演算步骤.
19 1.在△ 中,角 , , 所对的边分别为 , , ,且 = 4, = 5,cos = .
8
(1)求△ 的面积;(4分)
(2)求边长 及 sin 的值.(6分)
20. 统计某班同学一次考试的数学成绩,得到如下频率分布直方图,已知
该班学生数学成绩不低于 80分的频率为 0.60.
(1)求频率分布直方图中 , 的值;(4分)
(2)估计该班学生数学成绩的平均分和中位数.(6分)
第 3页,共 4页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
21. 某市为鼓励居民节约用电,采用阶梯电价的收费方式,当月用电量不
超过 100度的部分,按 0.4元/度收费;超过 100度的部分,按 0.8元/度收费.
(1)若某户居民用电量为 120度,则该月电费为多少元?(5分)
(2)若某户居民某月电费为 60元,则其用电量为多少度?(5分)
22. 如图,在正方体 1 1 1 1中, = 1.
(1)求证: //平面 1 1;(4分)
(2)求证: 1 ⊥平面 1 1;(4分)
(3)求直线 1 和平面 1 1所成的角.(4分)
试卷第 4页,共 4页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
参考答案:
1.C
【分析】由线面位置关系的判定,分析选项中结论是否正确.
【详解】A选项,缺条件 ,结论不成立;
B选项,直线 与直线 可能平行可能异面,结论不成立;
C选项,由直线与平面垂直的定义可知,结论正确
D选项,直线 可能与 平行,可能在 内,也可能与 相交,不一定满足垂直,结论不成立.
故选:C
2.B
【分析】计算出 1 = 3,从而求出 1 .
【详解】 1 = 1 + 2 = 3, 1 = 3 = 6 3 = 3.
故选:B
3.B
【分析】由题意确定出现一次 6点向上的概率,可得没有一次 6点向上的概率,利用对立事
件的概率关系求解即可.
1
【详解】将一颗质地均匀的骰子先后抛掷一次,出现一次 6点向上的概率为 ,
6
1 25
所以先后抛掷 2次,没有一次 6点向上的概率为(1 )2 = ,
6 36
25 11
所以至少出现一次 6点向上的概率为 1 = .
36 36
故选:B.
4.C
【分析】利用交集的定义求解.
【详解】集合 = ∣1 ≤ ≤ 3 , = { ∣2 < < 4},则 ∩ = { ∣2 < ≤ 3}.
故选:C.
5.C
【分析】利用函数的奇偶性定义判定即可.
1
【详解】对 A, = ≠ ,故 A不是偶函数;
对 B, = 3 = 3 ≠ ,故 B不是偶函数;
2
对 C, = 2的定义域为 R,关于原点对称,且 = = 2 = ,则其为偶函
数;
答案第 1页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
对 D, = 1 + ≠ ,故 D不是偶函数,
故选:C
6.D
【分析】由基本不等式求和的最小值.
1 1
【详解】已知 > 0,则 + ≥ 2 = 2,
1
当且仅当 = ,即 = 1 时等号成立,
则 + 1有最小值 2.
故选:D.
7.C
【分析】解一元二次不等式求得正确答案.
【详解】由 2 2 3 > 0 得 2 2 3 < 0,解得 1.5 < < 2,
所以原不等式的解集为{ ∣1.5 < < 2}.
故选:C
8.C
【分析】根据指数函数的性质即可得答案.
【详解】解:因为函数 = 的图象是下降的,所以 0 < < 1;
又因为函数 = 的图象是上升的,所以 > 1.
故选:C.
9.D
【分析】根据三角函数正弦定义相关知识可求.
【详解】因为角 的顶点与原点重合,始边与 轴的正半轴重合,点 (1, 3) 在角 的终边
上,
3 3 10
所以 sin = = ,
2 101 + 3 2
故选:D
10.D
【分析】根据互斥事件与对立事件的概念判断即可.
【详解】“甲、乙恰有一人中奖”与 互斥但不对立,故 A错误;
“甲、乙都没中奖”与 互斥但不对立,故 B错误;
答案第 2页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
“甲、乙至少有一人中奖”与 不互斥,故 C错误;
“甲、乙至多有一人中奖”与 互斥且对立,故 D正确.
故选:D.
11.A
【分析】根据三角函数图象平移变化可得.
π π
【详解】将函数 = sin + 的图象向右平移 个单位长度后,
3 6
π π π
所得图象对应的函数为 = sin + ,即 = sin + .
6 3 6
故选:A
12.C
【分析】利用平面向量的线性运算计算即可.
1 1 1
【详解】由题意可知 ��� �� = ��� �� = ��� �� � �� � = � � � � , ��� �� = ��� � + ��� �� = � �+ 1 � � � � =
2 2 2 2
1 � � + � � .
2
故选:C
13. = sin2 (答案不唯一)
【分析】根据三角函数周期公式确定 即可得答案.
【详解】由 = sin + 的周期为 = 2π = π,得 = 2,
不妨取 = 1, = 0,得一个满足题意的函数 = sin2 .
故答案为: = sin2 (答案不唯一)
14. 13
【分析】根据复数模的计算公式计算可得.
【详解】因为 = 2 3i,所以 = 22 + 3 2 = 13.
故答案为: 13
15 2π. / 2π
3 3
【分析】根据长方体外接球的特征即可求解半径,由体积公式即可求解.
【详解】根据长方体的结构特征可知长方体的体对角线为其外接球的一条直径 2 ,所以
3
2 = 2 = 2, 4 2故球的体积为 π × = 2π,
2 3 2 3
2π
故答案为:
3
答案第 3页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
16. 21
【分析】根据向量的模长公式直接代入求解即可.
2
【详解】 2� � + � � = 2� � + � � = 4� �2 + 4� � � � + � �2 = 4 × 4 + 4 × 2 × 1 × cos60° + 1 =
21,
故答案为: 21.
17.20
【分析】根据分层抽样的性质运算求解.
7
【详解】由题可知, = ,解得 = 20.
350 200+350+450
故答案为:20.
18. 1
【分析】根据奇函数定义求参数即可.
3+ 2 2 +1 3
【详解】因为 = 2 + =
2
2 + + 1, +1 +1
3
所以 = 2 + + 1,
2+1
则 + = 2 + 2,
因为 是奇函数,所以 + = 0,
所以 2 + 2 = 0,解得 = 1.
故答案为: 1
19.(1)15 7
4
(2) = 6 7,sin =
4
【分析】(1)利用平方关系和面积公式求解即可.
(2)利用余弦定理和正弦定理求解即可.
1
【详解】(1)由 cos = ,且 0 < < π,
8
3 7
则 sin = 1 cos2 = ,
8
1 15 7
所以 △ = sin = .2 4
(2)由 2 = 2 + 2 2 cos = 16 + 25 5 = 36,
则 = 6,
答案第 4页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
= sin = sin = 7又 ,则 .
sin sin 4
20.(1) = 0.02, = 0.01
(2)平均分、中位数分别为 81,82.5
【分析】(1)根据频率分布直方图的性质求解即可.
(2)利用平均数和中位数的定义和公式求解即可.
1 0.6【详解】( )由已知得 = 0.04 = 0.02,
10
则 0.005 + + 0.025 + 0.040 + 0.020 × 10 = 1,所以 = 0.01.
(2)该班学生数学成绩的平均分的估计值为:
55 × 0.005 + 65 × 0.01 + 75 × 0.025 + 85 × 0.04 + 95 × 0.02 × 10 = 81,
因为 0.005 + 0.01 + 0.025 × 10 = 0.4,
0.005 + 0.01 + 0.025 + 0.04 × 10 = 0.8,
所以中位数在 80,90 内.
0.5 0.4
故中位数为 80 + × 10 = 82.5.
0.4
21.(1)56
(2)125
【分析】(1)设用电量为 度,对应电费为 元,求出 关于 的分段函数,将 =120代入,
求解出该月电费;
(2)先判断出该户用电量超过了 100度,进而解方程,求出其用电量.
【详解】(1)设用电量为 度,对应电费为 元,
由题意得:当 ≤100时, =0.4 ;
当 >100时, =100×0.4+ 100 ×0.8=0.8 40,
即 = 0.4 , ≤1000.8 40, >100,
当 =120时, =0.8×120 40=56,
所以该月电费为 56元;
(2)因为 ≤100时, =0.4 ≤0.4×100=40<60,
所以该户用电量超过了 100度,
答案第 5页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
令 0.8 40=60,解得: =125,
故其用电量为 125度.
22.(1)证明见解析
(2)证明见解析
(3)30°
【分析】(1)由线面平行的判定可证明;
(2)先证明线线垂直,从而可得线面垂直;
(3)由(2)可得∠ 1 即为所求的角,再解三角形即可.
【详解】(1)证明:因为在正方体 1 1 1 1中,可知 // 1 1,而 平面 1 1,
1 1 平面 1 1,所以 //平面 1 1.
(2)证明:因为在正方体 1 1 1 1中,可知 1 1 ⊥平面 1 1 ,且 1 平面
1 1 ,所以 1 1 ⊥ 1,
又因为 1、 1 是正方形 1 1 的对角形,因此 1 ⊥ 1 ,
又 1 1 ∩ 1 = 1,且 1 1, 1 平面 1 1,
所以 1 ⊥平面 1 1.
(3)设 1与 1 的交点为 ,连接 1 ,由(2)可知直线 1 和平面 1 1所成的角为∠ 1 ,
且△ 1 为直角三角形,∠ 1 = 90°,
设正方体 1 1 1 1棱长为 2,可得 1 = 2 2, = 2,
所以∠ °1 = 30 ,因此直线 °1 和平面 1 1所成的角为30 .
答案第 6页,共 6页
{#{QQABSYQEggggQhBAARgCUQE4CAMQkAGACKoGAAAEoAABQRNABAA=}#}
同课章节目录
