方程的根和函数的零点浙江省温州市乐清市)
文档属性
| 名称 | 方程的根和函数的零点浙江省温州市乐清市) |  | |
| 格式 | rar | ||
| 文件大小 | 536.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-26 12:45:00 | ||
图片预览






文档简介
课件22张PPT。 3.1.1
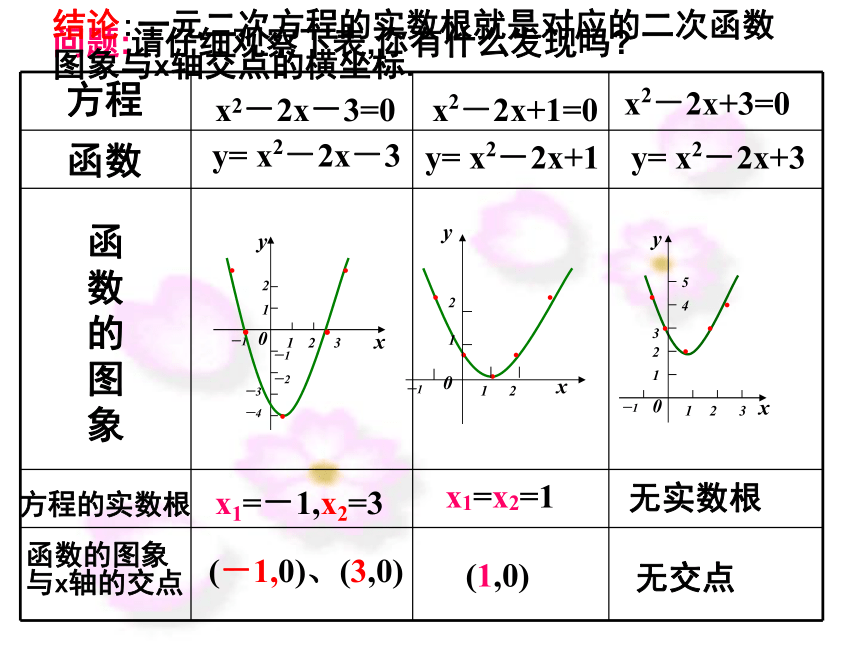
方程的根和函数的零点方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3问题:请仔细观察下表,你有什么发现吗?结论:一元二次方程的实数根就是对应的二次函数 图象与x轴交点的横坐标.方程ax2 +bx+c=0
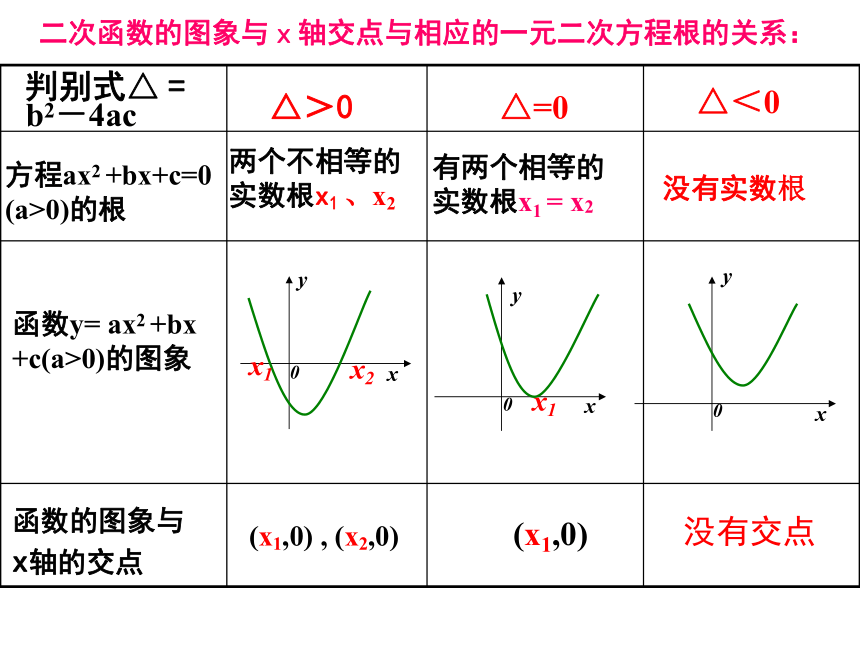
(a>0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象与
x轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等的
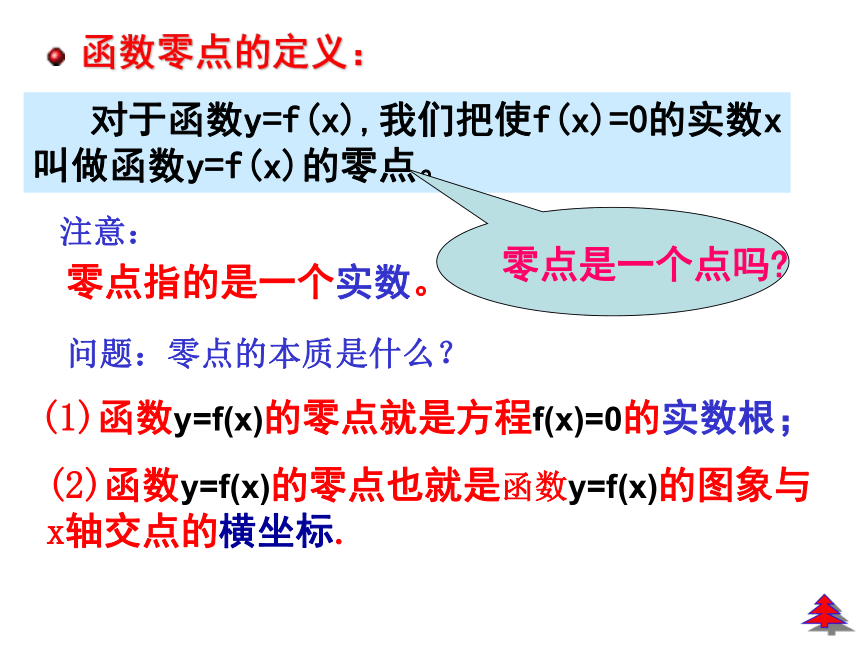
实数根x1 、x2二次函数的图象与x轴交点与相应的一元二次方程根的关系: 对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点。函数零点的定义:注意:零点指的是一个实数。问题:零点的本质是什么?(1)函数y=f(x)的零点就是方程f(x)=0的实数根;(2)函数y=f(x)的零点也就是函数y=f(x)的图象与x轴交点的横坐标.方程f(x)=0有实数根因此,有如下等价关系:“数”“形”因此,求函数的零点有两种方法.例1 求下列函数的零点(1)f(x)=x3-x(2)f(x)=2x-1答(1)-1,0,1答(2)0答(3)无零点[思路]方法一:解方程方法二:作出函数的图象012345-1-212345-1-2-3-4xy[探究]观察二次函数f(x)=x2-2x-3的图象,回答下列问题:
f(x)=x2-2x-3在区间[-2,1]上有零点 ,
f(-2)= ,f(1)= ,
则乘积f(-2) f(1) 0.
(2) f(x)=x2-2x-3在区间[2,4]上
有零点 ,f(2)= ,f(4)= ,
则乘积f(2) f(4) 0.一般地,如果函数f(x)在区间[a,b]上有唯一零点c,
则f(a)f(b) 0.-15-4<3-35<思考1:如果函数f(x)在区间[a,b]上满足f(a)f(b)<0,则函数f(x)在区间[a,b]上一定有零点吗?前提:函数f(x)的图象在区间[a,b]上必须是连续
不断的.思考2:如果函数f(x)在区间[a,b]上有零点, 则f(a)f(b)<0一定成立吗?前提:函数f(x)的图象在区间[a,b]上必须是单调的.结论例2 求函数f(x)=lnx+2x-6的零点个数.解:用计算器或计算机作出x、f(x)的对应值表(表3--1)和图象(图3.1--3). x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972 表3--1图3.1--3课堂练习2: 课堂小结: 课后作业:
1、求下列函数的零点:(1)y=-x2+6x+7;
(2)y=x3-4x。
2、若函数f(x)=x2-ax-b的两个零点是2和3,求 loga25+ b2。1、函数零点的定义;2、函数的零点与方程的根的关系;3、确定函数的零点的方法。XYAMBO10m(1,40/3)(0,10)?课堂练习1:利用函数图象判断下列方程有没有根,有几个根:(1)-x2+3x+5=0;(2)2x(x-2)=-3;(3) x2 =4x-4;(4)5 x2 +2x=3 x2 +5.y=-x2-x+20; (2)y=2x-1; 拓展:求下列函数的零点。 评注:求函数的零点就是求相应的方程的根,一般可以借助求根公式或因式分解等办法,求出方程的根,从而得出函数的零点。
方程的根和函数的零点方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3问题:请仔细观察下表,你有什么发现吗?结论:一元二次方程的实数根就是对应的二次函数 图象与x轴交点的横坐标.方程ax2 +bx+c=0
(a>0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象与
x轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等的
实数根x1 、x2二次函数的图象与x轴交点与相应的一元二次方程根的关系: 对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点。函数零点的定义:注意:零点指的是一个实数。问题:零点的本质是什么?(1)函数y=f(x)的零点就是方程f(x)=0的实数根;(2)函数y=f(x)的零点也就是函数y=f(x)的图象与x轴交点的横坐标.方程f(x)=0有实数根因此,有如下等价关系:“数”“形”因此,求函数的零点有两种方法.例1 求下列函数的零点(1)f(x)=x3-x(2)f(x)=2x-1答(1)-1,0,1答(2)0答(3)无零点[思路]方法一:解方程方法二:作出函数的图象012345-1-212345-1-2-3-4xy[探究]观察二次函数f(x)=x2-2x-3的图象,回答下列问题:
f(x)=x2-2x-3在区间[-2,1]上有零点 ,
f(-2)= ,f(1)= ,
则乘积f(-2) f(1) 0.
(2) f(x)=x2-2x-3在区间[2,4]上
有零点 ,f(2)= ,f(4)= ,
则乘积f(2) f(4) 0.一般地,如果函数f(x)在区间[a,b]上有唯一零点c,
则f(a)f(b) 0.-15-4<3-35<思考1:如果函数f(x)在区间[a,b]上满足f(a)f(b)<0,则函数f(x)在区间[a,b]上一定有零点吗?前提:函数f(x)的图象在区间[a,b]上必须是连续
不断的.思考2:如果函数f(x)在区间[a,b]上有零点, 则f(a)f(b)<0一定成立吗?前提:函数f(x)的图象在区间[a,b]上必须是单调的.结论例2 求函数f(x)=lnx+2x-6的零点个数.解:用计算器或计算机作出x、f(x)的对应值表(表3--1)和图象(图3.1--3). x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972 表3--1图3.1--3课堂练习2: 课堂小结: 课后作业:
1、求下列函数的零点:(1)y=-x2+6x+7;
(2)y=x3-4x。
2、若函数f(x)=x2-ax-b的两个零点是2和3,求 loga25+ b2。1、函数零点的定义;2、函数的零点与方程的根的关系;3、确定函数的零点的方法。XYAMBO10m(1,40/3)(0,10)?课堂练习1:利用函数图象判断下列方程有没有根,有几个根:(1)-x2+3x+5=0;(2)2x(x-2)=-3;(3) x2 =4x-4;(4)5 x2 +2x=3 x2 +5.y=-x2-x+20; (2)y=2x-1; 拓展:求下列函数的零点。 评注:求函数的零点就是求相应的方程的根,一般可以借助求根公式或因式分解等办法,求出方程的根,从而得出函数的零点。
