2.1.2指数函数及其性质 (一)(必修1)(浙江省温州市)
文档属性
| 名称 | 2.1.2指数函数及其性质 (一)(必修1)(浙江省温州市) |  | |
| 格式 | rar | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-26 14:56:00 | ||
图片预览









文档简介
课件34张PPT。2.1.2 指数函数及其性质
材料1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个……一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x的函数关系是什么?分析24816细胞分裂次数与细胞个数的函数关系是
y=2x材料2:当生物死后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系,这个关系式应该怎样表示呢?思考你能从以上两个解析式中抽象出一个更具有一般性的函数模型吗?y=ax(a>0,a≠1),这就是我们下面所要研究的一类重要函数模型--- 。指数函数1.指数函数 函数y=ax(a?0,且a?1)叫做指数函数,其中x是自变量,函数的定义域是R.问题.为何规定a?0,且a?1?当a?0时,ax有些会没有意义,
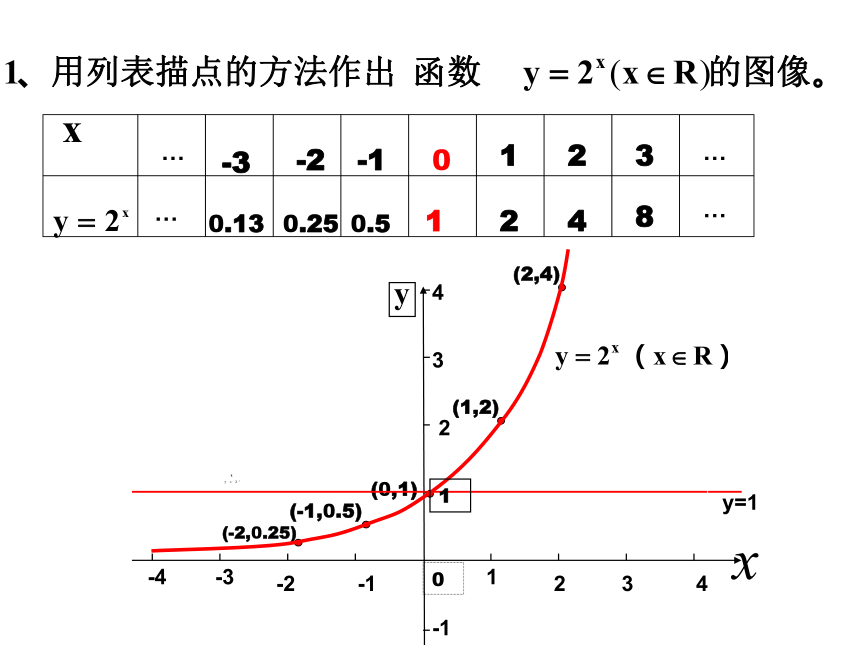
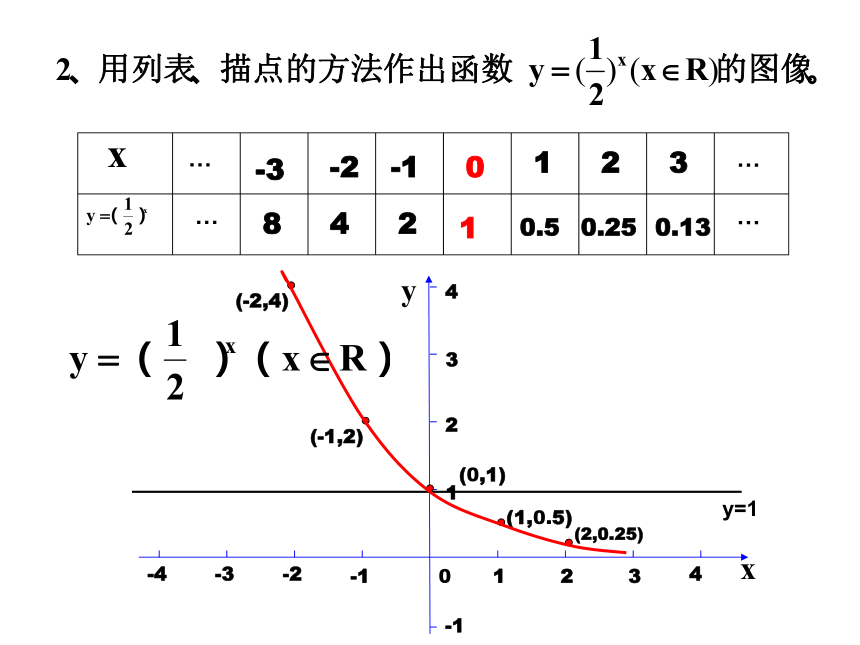
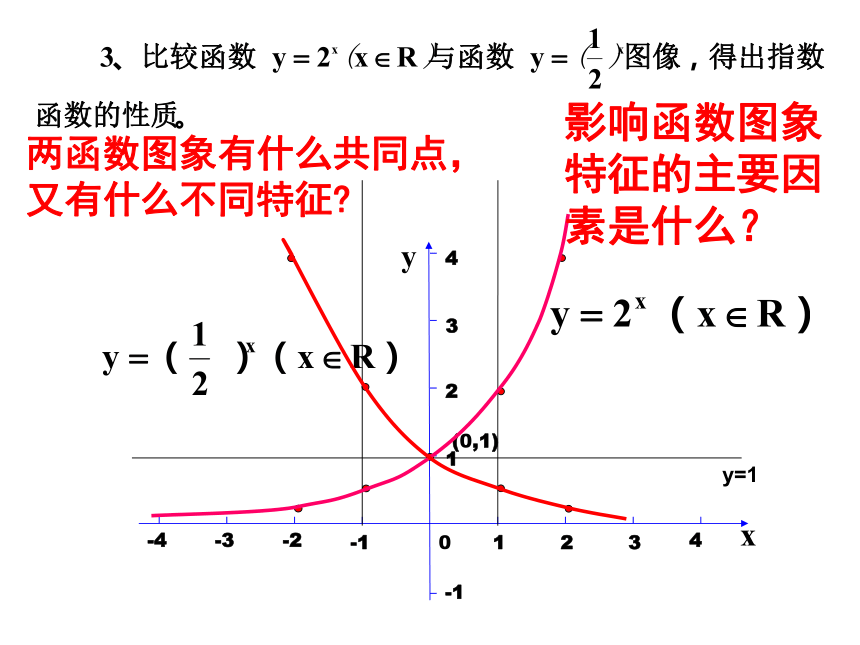
如 , 等都没有意义;(2)而当a=1时,函数值y恒等于1,没有研究的必要.为了便于研究,规定:a>0 且a≠1练习:判断下列函数是否是指数函数2.指数函数的图象和性质设问2:我们研究函数的性质,通常都研究哪几个性 质?设问1:得到函数的图象一般用什么方法?列表、求对应的x和y值、描点作图 y=1两函数图象有什么共同点,又有什么不同特征?影响函数图象特征的主要因素是什么?R(0,+∞)(0,1)在R上是增函数在R上是减函数当x>0,y>1当x=0 ,y=1当x<0,y <1当x>0 ,y<1当x=0 ,y=1当x<0,y>1指数函数y=ax (a>0,且a≠1)的图象和性质:y=2x思考结论:两个函数图象关于y轴对称例6 已知指数函数f(x)=ax (a>0,且a≠1)的图象经过点(3,π),求f(0)、f(1)、f(-3)的值.例题与练习练习1、已知y=f(x)是指数函数,且f(2)=4,求函数y=f(x)的解析式。练习2、已知y=(2a-1)x是指数函数,求实数a的取值范围。练习3、已知f(x)=ax+b-1 (其中a>0且a≠1),的图象过第一、三、四象限,则一定有( )
(A)0<a < 1,b>0, (B)a >1, b>0
(C)0<a < 1,b<0 (D)a >1, b<0
D练习4、函数f(x)=3x-5+1 的图象必过点( )
(A)(0,1) (B)(5,1)
(C)(5,2) (D)(1,5)
C例7.比较下列各题中两个值的大小:(1)1.7 2.5 ,1.7 3 (2)0.8 – 0.1 ,0.8 – 0.2 (3)1.7 0.3 ,0.9 3.1解:(1)考察指数函数y=1.7 x .由于底数1.7>1 ,所以指数函数在R上是增函数. ∵2.5<3 ∴1.7 2.5<1.7 3(2)0.8 – 0.1<0.8 – 0.2(3)由指数函数的性质知
1.7 0.3>1.7 0=1 , 0.9 3.1<0.9 0=1即1.7 0.3>1 , 0.9 3.1<1 ,∴1.7 0.3>0.9 3.1 .此题两数底数不同,无法直接比较大小,因此我们想到找一个中间变量,通过与中间变量比较,最后得出两数的情况.练习1:设y1=a3x+1,y2=a-2x,其中a>0且a?1,
确定x为何值时,有
1)y1=y2 (2)y1>y2练习2:如果函数f(x)=(1-2a)x在实数集R上是减函数,那么实数a的取值范围是 .(0,0.5)解:D例8、指数函数的图象如下图所示,则底数
a,b,c,d与正整数1共五个数,从大到小的
顺序是: 。DR(0,+∞)(0,1)在R上是增函数在R上是减函数当x>0,y>1当x=0 ,y=1当x<0,y <1当x>0 ,y<1当x=0 ,y=1当x<0,y>1指数函数y=ax (a>0,且a≠1)的图象和性质:例9.求下列函数的定义域、值域:解: ∴函数的定义域为{x|x ? 0},
值域为{y |y>0 ,且y?1}.值域为(0,1] .例10、求函数y=4-x-2-x+1的值域.变式:求函数y=4-x-2-x+1,x∈[-3,2]的值域.练习:已知函数y=a2x+2ax-1(a>1)在区间
[-1,1]上的最大值为14,求a的值.练习答:a=3变式2、试利用函数y=2x的图象作出函数
y=2x-1+1的图象,并求值域及单调区间。综合题:设函数f(x)=ax-a-x(0<a<1)
(1)试判断函数的奇偶性;
(2)试判断函数的单调性,并给出证明;
(3)若f(1-m)+ f(1-m2) >0,求实数m的取值范围。变式:若将条件 “0<a<1 ”改为“a>0且a≠0”,
那结果又如何?例13、截止到1999年底,我国人口约13亿。如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?y= 13(1+1%)x1、指数函数的定义。
2、指数函数简图的作法以及应注意的地方。
3、指数函数的图像和性质。小结2.指数函数的图象和性质1.图象全在x轴上方,与x轴无限接近。1.定义域为R,值域为(0,+?).2.图象过定点(0,1)2.当x=0时,y=13.自左向右图象逐渐上升3.自左向右图象逐渐下降3.在R上是增函数3.在R上是减函数4.图象分布在左下和右上两个区域内4.图象分布在左上和右下两个区域内4.当x>0时,y>1;当x<0时,00时, 01.5.图象无对称性(既不关于原点对称,也不关于y轴对称)5.既不是奇函数也不是偶函数.y=ax (a>0,a≠1)叫做指数函数x∈Ry∈R+
非奇非偶a>1,增00,y>1
x<0,00,0x<0,y>12、1 y=10xy=2xy=x4.2 指数函数 y = a x ( a < 0, 且 a ≠0 )一般性质:(1)图像沿 x 轴 向左右方向无限延伸,
函数的 定义域为 R 。 (2)图像都在 x 轴上方,函数的值域是R+,(3)图像都经过 点(0 ,1 ), 即 f (0 ) = 1(4)当 a >1 时, 在 (-∞,+ ∞)上是增函数;
0xy(5)当 a >1 时,若 x > 0 , 则 y >1
(a 越大,图像上方越较靠近 y 轴 )若 x < 0 , 则 0当 0 0 , 则 01
(a 越小,图像上方越较靠近 y 轴 )
当 0 当x > 0,0 x<0 , y>10 < a < 1
指数函数的图象和性质
y=2x材料2:当生物死后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系,这个关系式应该怎样表示呢?思考你能从以上两个解析式中抽象出一个更具有一般性的函数模型吗?y=ax(a>0,a≠1),这就是我们下面所要研究的一类重要函数模型--- 。指数函数1.指数函数 函数y=ax(a?0,且a?1)叫做指数函数,其中x是自变量,函数的定义域是R.问题.为何规定a?0,且a?1?当a?0时,ax有些会没有意义,
如 , 等都没有意义;(2)而当a=1时,函数值y恒等于1,没有研究的必要.为了便于研究,规定:a>0 且a≠1练习:判断下列函数是否是指数函数2.指数函数的图象和性质设问2:我们研究函数的性质,通常都研究哪几个性 质?设问1:得到函数的图象一般用什么方法?列表、求对应的x和y值、描点作图 y=1两函数图象有什么共同点,又有什么不同特征?影响函数图象特征的主要因素是什么?R(0,+∞)(0,1)在R上是增函数在R上是减函数当x>0,y>1当x=0 ,y=1当x<0,y <1当x>0 ,y<1当x=0 ,y=1当x<0,y>1指数函数y=ax (a>0,且a≠1)的图象和性质:y=2x思考结论:两个函数图象关于y轴对称例6 已知指数函数f(x)=ax (a>0,且a≠1)的图象经过点(3,π),求f(0)、f(1)、f(-3)的值.例题与练习练习1、已知y=f(x)是指数函数,且f(2)=4,求函数y=f(x)的解析式。练习2、已知y=(2a-1)x是指数函数,求实数a的取值范围。练习3、已知f(x)=ax+b-1 (其中a>0且a≠1),的图象过第一、三、四象限,则一定有( )
(A)0<a < 1,b>0, (B)a >1, b>0
(C)0<a < 1,b<0 (D)a >1, b<0
D练习4、函数f(x)=3x-5+1 的图象必过点( )
(A)(0,1) (B)(5,1)
(C)(5,2) (D)(1,5)
C例7.比较下列各题中两个值的大小:(1)1.7 2.5 ,1.7 3 (2)0.8 – 0.1 ,0.8 – 0.2 (3)1.7 0.3 ,0.9 3.1解:(1)考察指数函数y=1.7 x .由于底数1.7>1 ,所以指数函数在R上是增函数. ∵2.5<3 ∴1.7 2.5<1.7 3(2)0.8 – 0.1<0.8 – 0.2(3)由指数函数的性质知
1.7 0.3>1.7 0=1 , 0.9 3.1<0.9 0=1即1.7 0.3>1 , 0.9 3.1<1 ,∴1.7 0.3>0.9 3.1 .此题两数底数不同,无法直接比较大小,因此我们想到找一个中间变量,通过与中间变量比较,最后得出两数的情况.练习1:设y1=a3x+1,y2=a-2x,其中a>0且a?1,
确定x为何值时,有
1)y1=y2 (2)y1>y2练习2:如果函数f(x)=(1-2a)x在实数集R上是减函数,那么实数a的取值范围是 .(0,0.5)解:D例8、指数函数的图象如下图所示,则底数
a,b,c,d与正整数1共五个数,从大到小的
顺序是: 。DR(0,+∞)(0,1)在R上是增函数在R上是减函数当x>0,y>1当x=0 ,y=1当x<0,y <1当x>0 ,y<1当x=0 ,y=1当x<0,y>1指数函数y=ax (a>0,且a≠1)的图象和性质:例9.求下列函数的定义域、值域:解: ∴函数的定义域为{x|x ? 0},
值域为{y |y>0 ,且y?1}.值域为(0,1] .例10、求函数y=4-x-2-x+1的值域.变式:求函数y=4-x-2-x+1,x∈[-3,2]的值域.练习:已知函数y=a2x+2ax-1(a>1)在区间
[-1,1]上的最大值为14,求a的值.练习答:a=3变式2、试利用函数y=2x的图象作出函数
y=2x-1+1的图象,并求值域及单调区间。综合题:设函数f(x)=ax-a-x(0<a<1)
(1)试判断函数的奇偶性;
(2)试判断函数的单调性,并给出证明;
(3)若f(1-m)+ f(1-m2) >0,求实数m的取值范围。变式:若将条件 “0<a<1 ”改为“a>0且a≠0”,
那结果又如何?例13、截止到1999年底,我国人口约13亿。如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?y= 13(1+1%)x1、指数函数的定义。
2、指数函数简图的作法以及应注意的地方。
3、指数函数的图像和性质。小结2.指数函数的图象和性质1.图象全在x轴上方,与x轴无限接近。1.定义域为R,值域为(0,+?).2.图象过定点(0,1)2.当x=0时,y=13.自左向右图象逐渐上升3.自左向右图象逐渐下降3.在R上是增函数3.在R上是减函数4.图象分布在左下和右上两个区域内4.图象分布在左上和右下两个区域内4.当x>0时,y>1;当x<0时,0
非奇非偶a>1,增0
x<0,0
函数的 定义域为 R 。 (2)图像都在 x 轴上方,函数的值域是R+,(3)图像都经过 点(0 ,1 ), 即 f (0 ) = 1(4)当 a >1 时, 在 (-∞,+ ∞)上是增函数;
0xy(5)当 a >1 时,若 x > 0 , 则 y >1
(a 越大,图像上方越较靠近 y 轴 )若 x < 0 , 则 0
(a 越小,图像上方越较靠近 y 轴 )
当 0
指数函数的图象和性质
