2.2.1对数的运算(浙江省温州市)
文档属性
| 名称 | 2.2.1对数的运算(浙江省温州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 206.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-26 00:00:00 | ||
图片预览


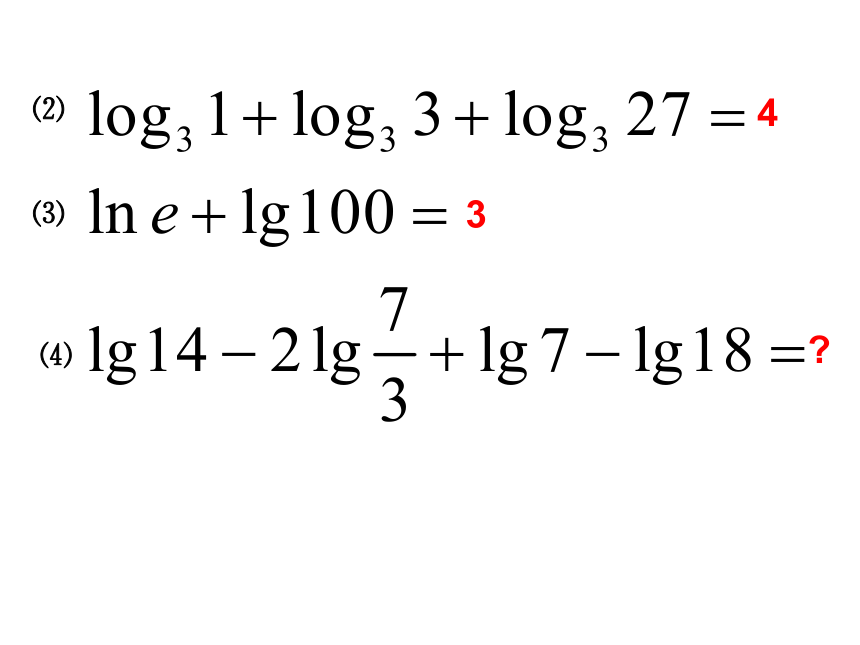






文档简介
课件26张PPT。对数有关性质: ⑴负数与零没有对数(∵在指数式中 N > 0 ) ⑵ ⑶对数恒等式[复习]⑷常用对数: 简记作lgN。 ⑸自然对数: 简记作lnN。 (6)底数a的取值范围: 真数N的取值范围 :[课前练习]:⑴给出四个等式:其中正确的是________1) ,2)3?42.2.1 对数与对数运算
第二课 对数的运算 问题1:(1)试用log24与log28表示log24×8
(2)试用log39与log381表示log39×81问题2:试猜想logaMN与logaM,logaN之间的关
系?(其中a>0且a≠1,M>0 ,N>0) 猜想:如果 a>0,a?1,M>0,N>0,则有:[问题探究]证明:设 由对数的定义可以得: ∴MN= 即证得 命题1:如果 a>0,a?1,M>0,N>0,则有:上述证明是运用转化的思想,先通过假设,
将对数式化成指数式,并利用幂的运算性
质进行恒等变形;然后再根据对数定义将
指数式化成对数式。对数运算法则:如果a>0,a ?1,M>0,N>0,那么:证明:设 由对数的定义可以得: ∴ 即证得 命题2:如果a>0,a ?1,M>0,N>0,那么:证明:设 由对数的定义可以得: ∴即证得 命题3:如果a>0,a ?1,M>0,N>0,那么:小结:对数运算法则如果a>0,a ?1,M>0,N>0,那么:①简易语言表达:“积的对数 = 对数的和”……②真数的取值范围必须是③注意逆向运用公式 ④对公式容易错误记忆,要特别注意:例1 讲解范例 解(1) (2) 用 表示下列各式: 例2 计算(1) (2) 讲解范例 解:=5+14=19解:用lgx,lgy,lgz表示下列各式:练习1. (1) (4) (3) (2) =lgx+2lgy-lgz;=lgx+lgy+lgz;=lgx+3lgy- lgz; 练习2.求下列各式的值: (1) (4) (3) (2) ⑴ 若⑵ 的值为______⑶练习3:2(4) = . 0(1) 练习4计算: 解: 其他重要公式1:证明:设 由对数的定义可以得: 即证得 真数的指数直接拿到前面,
底数的指数倒数后拿到前面。其他重要公式2:证明:设 由对数的定义可以得: 即证得 这个公式叫做换底公式其他重要公式3:证明:由换底公式 取以b为底的对数得: 还可以变形,得 练习4 求 解:=3小结:对数运算法则:如果 a >0,a ?1,M >0,N >0 , 有:其他重要公式:探究: 证明:换底公式的证明证明:证明:对数的运算性质说明:2) 有时可逆向运用公式3)真数的取值必须是(0,+∞)4)注意≠≠如果 a > 0,a ? 1,M > 0, N > 0 有:1) 简易语言表达:”积的对数=对数的和”……
课堂小结:
第二课 对数的运算 问题1:(1)试用log24与log28表示log24×8
(2)试用log39与log381表示log39×81问题2:试猜想logaMN与logaM,logaN之间的关
系?(其中a>0且a≠1,M>0 ,N>0) 猜想:如果 a>0,a?1,M>0,N>0,则有:[问题探究]证明:设 由对数的定义可以得: ∴MN= 即证得 命题1:如果 a>0,a?1,M>0,N>0,则有:上述证明是运用转化的思想,先通过假设,
将对数式化成指数式,并利用幂的运算性
质进行恒等变形;然后再根据对数定义将
指数式化成对数式。对数运算法则:如果a>0,a ?1,M>0,N>0,那么:证明:设 由对数的定义可以得: ∴ 即证得 命题2:如果a>0,a ?1,M>0,N>0,那么:证明:设 由对数的定义可以得: ∴即证得 命题3:如果a>0,a ?1,M>0,N>0,那么:小结:对数运算法则如果a>0,a ?1,M>0,N>0,那么:①简易语言表达:“积的对数 = 对数的和”……②真数的取值范围必须是③注意逆向运用公式 ④对公式容易错误记忆,要特别注意:例1 讲解范例 解(1) (2) 用 表示下列各式: 例2 计算(1) (2) 讲解范例 解:=5+14=19解:用lgx,lgy,lgz表示下列各式:练习1. (1) (4) (3) (2) =lgx+2lgy-lgz;=lgx+lgy+lgz;=lgx+3lgy- lgz; 练习2.求下列各式的值: (1) (4) (3) (2) ⑴ 若⑵ 的值为______⑶练习3:2(4) = . 0(1) 练习4计算: 解: 其他重要公式1:证明:设 由对数的定义可以得: 即证得 真数的指数直接拿到前面,
底数的指数倒数后拿到前面。其他重要公式2:证明:设 由对数的定义可以得: 即证得 这个公式叫做换底公式其他重要公式3:证明:由换底公式 取以b为底的对数得: 还可以变形,得 练习4 求 解:=3小结:对数运算法则:如果 a >0,a ?1,M >0,N >0 , 有:其他重要公式:探究: 证明:换底公式的证明证明:证明:对数的运算性质说明:2) 有时可逆向运用公式3)真数的取值必须是(0,+∞)4)注意≠≠如果 a > 0,a ? 1,M > 0, N > 0 有:1) 简易语言表达:”积的对数=对数的和”……
课堂小结:
