26.1.2反比例函数的图象和性质课件(共50张PPT) 人教版数学九年级下册
文档属性
| 名称 | 26.1.2反比例函数的图象和性质课件(共50张PPT) 人教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 00:00:00 | ||
图片预览


文档简介
(共50张PPT)
反比例函数的图象和性质
学习目标
反比例函数的图象和性质
体会并了解反比例函数图象的意义;
进一步熟悉作函数图象的步骤,会用描点法作反比例函数的图象;
经历画图、观察、猜想、思考等数学活动,向学生渗透数形结合的思想;
通过观察图象分析其性质,培养学生的探究、归纳及概括的能力.
重点
难点
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
一次函数图象
二次函数图象
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
反比例函数图象
描点法
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
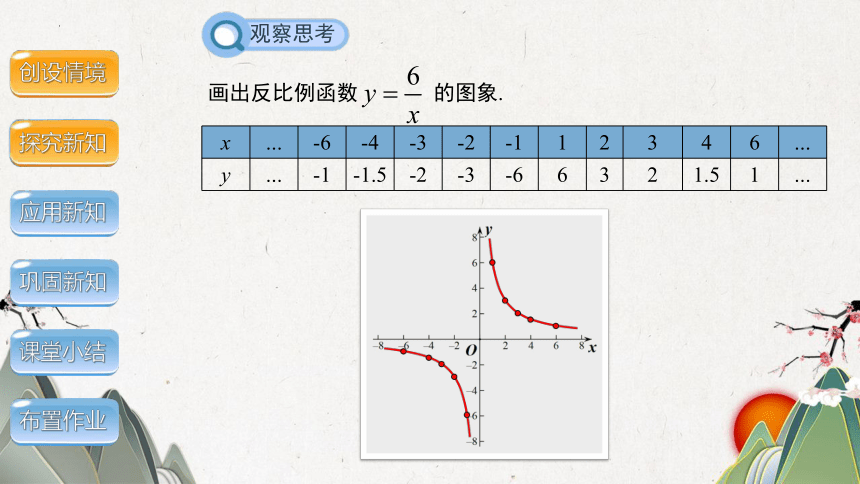
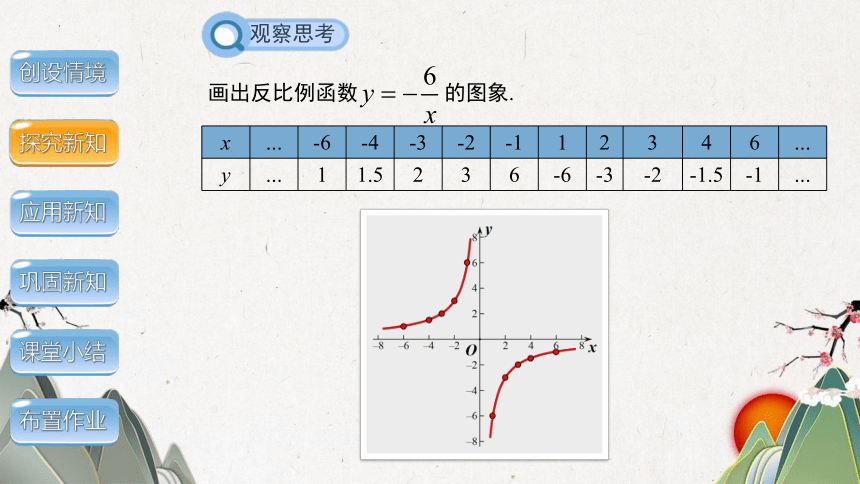
x … -6 -4 -3 -2 -1 1 2 3 4 6 …
y … -1 -1.5 -2 -3 -6 6 3 2 1.5 1 …
画出反比例函数 的图象.
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
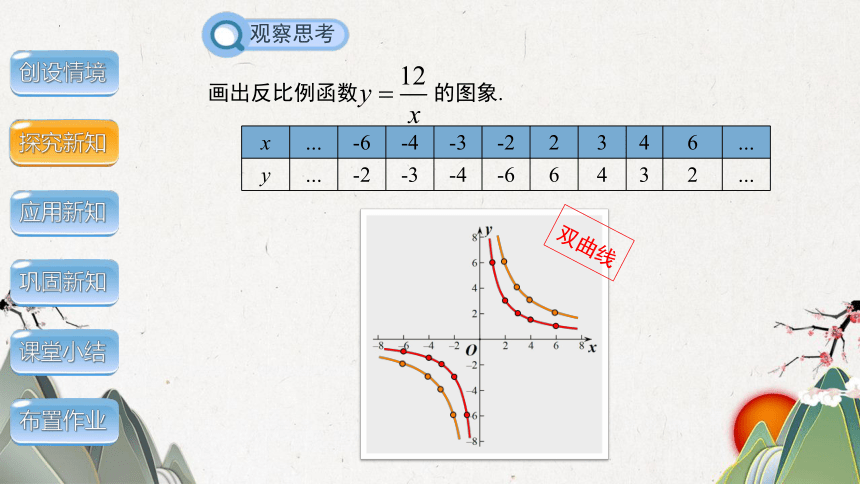
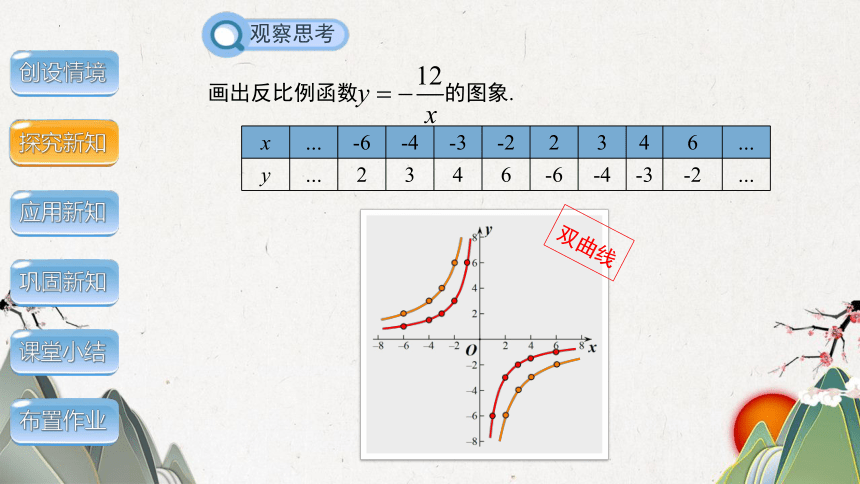
x … -6 -4 -3 -2 2 3 4 6 …
y … -2 -3 -4 -6 6 4 3 2 …
画出反比例函数 的图象.
双曲线
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
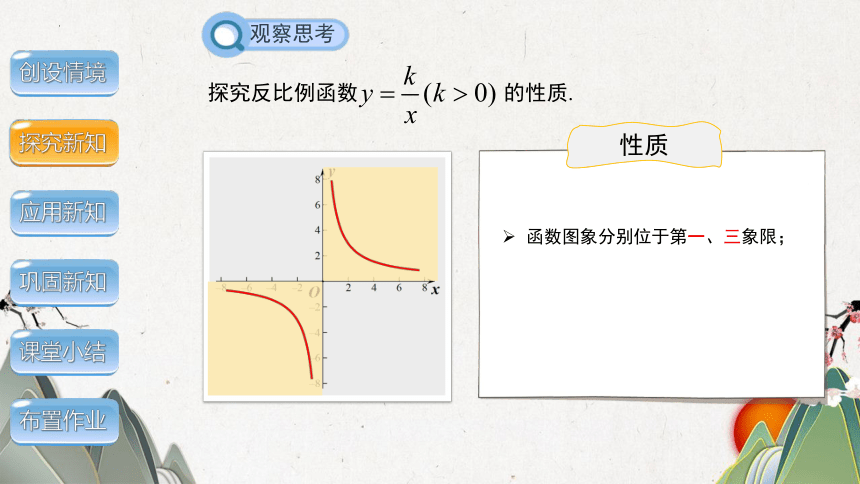
探究反比例函数 的性质.
性质
函数图象分别位于第一、三象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
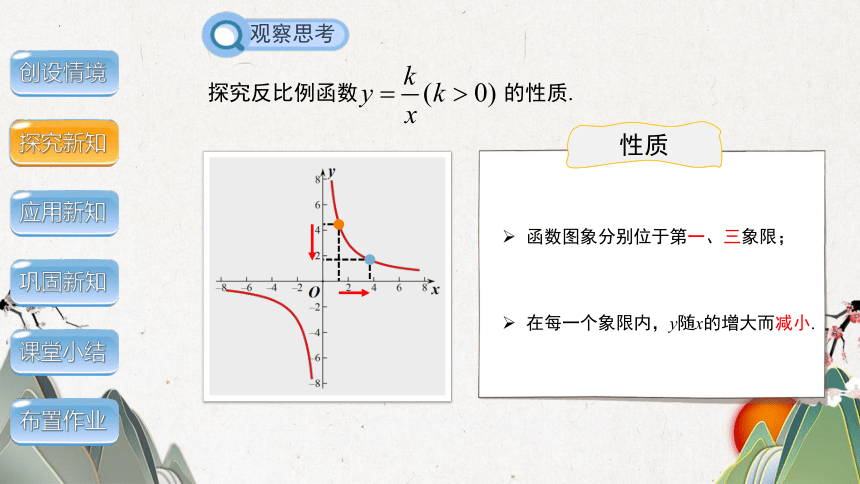
探究反比例函数 的性质.
性质
在每一个象限内,y随x的增大而减小.
函数图象分别位于第一、三象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
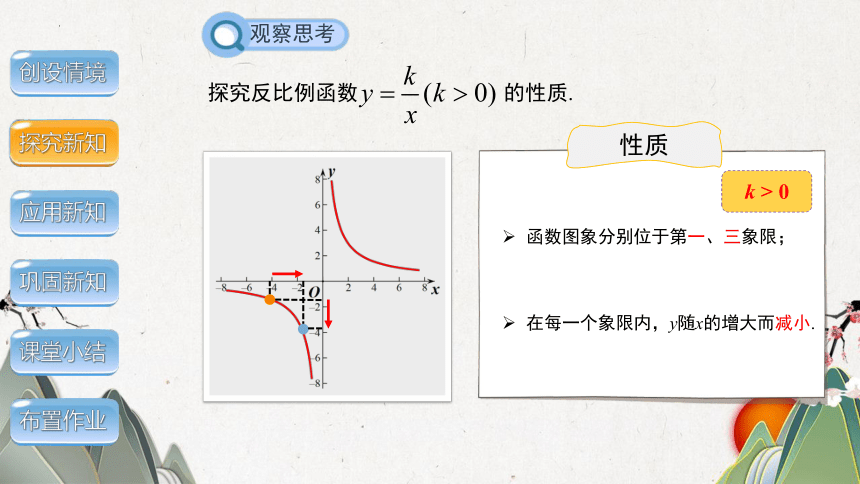
探究反比例函数 的性质.
性质
k > 0
在每一个象限内,y随x的增大而减小.
函数图象分别位于第一、三象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
x … -6 -4 -3 -2 -1 1 2 3 4 6 …
y … 1 1.5 2 3 6 -6 -3 -2 -1.5 -1 …
画出反比例函数 的图象.
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
x … -6 -4 -3 -2 2 3 4 6 …
y … 2 3 4 6 -6 -4 -3 -2 …
画出反比例函数 的图象.
双曲线
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
性质
探究反比例函数 的性质.
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
函数图象分别位于第二、四象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质
性质
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
k < 0
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
反比例函数
性质
k < 0
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
反比例函数
双曲线
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
典型例题
例1.如图所示的图象对应的函数解析式为( )
A.
B.
C.
D.
D
双曲线
k<0
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
B
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例3.已知双曲线 ,当x>0时,y随x的增大而增大,
则m的取值范围是 .
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例3.已知双曲线 ,当x>0时,y随x的增大而增大,
则m的取值范围是 .
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例3.已知双曲线 ,当x>0时,y随x的增大而增大,
则m的取值范围是 .
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
典型例题
随堂练习
练1.反比例函数 的图象位于( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
D
k=-4<0
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练2.下列反比例函数中,其图象的一个分支
一定在第三象限的是( )
(A)
(B)
(C)
(D)
(m为常数,且m≠-2)
(a为常数,且a≠±1)
C
k > 0
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练3.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数
的图象上,且x1”或“<”).
<
x1
x2
y1
y2
P1
P2
图象
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
随堂练习
反比例函数的图象和性质
性质
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
反比例函数的图象和性质
学习目标
反比例函数的图象和性质
进一步理解和掌握反比例函数的图象与性质;
灵活运用反比例函数的图象和性质解决问题;
领会反比例函数的解析式与图象的联系,体会数形结合与转化的思想方法;
体验数学活动中的探索性和创造性,感受数学美,激发学习兴趣.
重点
难点
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
反比例函数
双曲线
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
下列反比例函数:
想一想
(1)图象位于第一、三象限的是 ;
(2)图象位于第二、四象限的是 .
④
①
②
③
k > 0 函数图象分别位于一、三象限;
k < 0 函数图象分别位于二、四象限.
①
②
③
④
④
①
②
③
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
下列反比例函数:
想一想
(3)若0(4)若x1y2的函数是 ;
④
①
②
③
④
①
②
③
k > 0 在每一个象限内,y随x的增大而减小;
k < 0 在每一个象限内,y随x的增大而增大.
①
③
②
④
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
下列反比例函数:
想一想
(3)若0(4)若x1y2的函数是 ;
④
①
②
③
④
①
②
③
①
③
②
④
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
数形结合
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例1.已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于第几象限?y随x的增大如何变化?
y随x的变化情况与哪个量有关?
图象的位置由哪个量确定?
点在图象上意味着什么?
如何求这个量?
点A的坐标满足函数解析式
待定系数法
k > 0 函数图象分别位于一、三象限;
k < 0 函数图象分别位于二、四象限.
k > 0 在每一个象限内,y随x的增大而减小;
k < 0 在每一个象限内,y随x的增大而增大.
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例1.已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于第几象限?y随x的增大如何变化?
解:
设反比例函数的解析式为 ;
∵反比例函数的图象经过点A(2,6);
∴
,解得 ;
∴函数的图象分别位于第一、三象限,
在每个象限内,y随x的增大而减小.
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
解:
由(1)知反比例函数的解析式为 ;
分别将点B(3,4), ,D(2,5)代入;
当 时,
,所以点B在反比例函数的图象上;
当 时,
,所以点C在反比例函数的图象上;
当 时,
,所以点D不在反比例函数的图象上.
例1.已知反比例函数的图象经过点A(2,6).
(2)点B(3,4), ,D(2,5)是否在这个函数的图象上?
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
k > 0 函数图象分别位于一、三象限.
图象的另一支位于第三象限
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
解:(1)∵这个函数的图象的一支位于第一象限
∴另一支必位于第三象限
∵这个函数的图象位于第一、三象限
∴ ,即
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(2)在这个函数图象的某一支上任取点A(x1,y1)和点B(x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
k > 0 在每一个象限内,y随x的增大而减小.
x1
x2
y1
y2
A
B
y1巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
k > 0 在每一个象限内,y随x的增大而减小.
x1
x2
y1
y2
A
B
y1例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(2)在这个函数图象的某一支上任取点A(x1,y1)和点B(x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(2)在这个函数图象的某一支上任取点A(x1,y1)和点B(x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
解:(2)∵
∴在这个函数图象的任一支上,
y随x的增大而减小
∴当 x1>x2时,y1课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练1.已知反比例的图象经过点A(1,-6).
(1)这个函数的图象位于第几象限?
在图象的每一支上,y随x的增大如何变化?
(2)点B(2,3),C(3,2), 是否在这个函数的图象上?
为什么?
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练1.已知反比例的图象经过点A(1,-6).
(1)这个函数的图象位于第几象限?
在图象的每一支上,y随x的增大如何变化?
解:
设反比例函数的解析式为 ;
∵反比例函数的图象经过点A(1,-6);
∴
,解得 ;
∴函数的图象分别位于第二、四象限,
在每个象限内,y随x的增大而增大.
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练1.已知反比例的图象经过点A(1,-6).
(2)点B(2,3),C(3,2), 是否在这个函数的图象上?
为什么?
解:
由(1)知反比例函数的解析式为 ;
分别将点B(2,-3),C(3,2), 代入;
当 时,
,所以点B在反比例函数的图象上;
当 时,
,所以点C不在反比例函数的图象上;
当 时,
,所以点D在反比例函数的图象上.
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练2.若点A(-2,a),B(-1,b),C(3,c)都在反比例函数
图象上,a,b,c有怎样的大小关系?
a
b
c
c课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练2.若点A(-2,a),B(-1,b),C(3,c)都在反比例函数
图象上,a,b,c有怎样的大小关系?
解:
∵k < 0;
∴反比例函数的图象分别位于第二、四象限;
且在每个象限内,y随x的增大而增大;
∵-2 < -1 < 0 < 3;
∴c < 0 < a < b.
图象
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
随堂练习
反比例函数的图象和性质
性质
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
数形结合
反比例函数的图象和性质
学习目标
反比例函数的图象和性质
体会并了解反比例函数图象的意义;
进一步熟悉作函数图象的步骤,会用描点法作反比例函数的图象;
经历画图、观察、猜想、思考等数学活动,向学生渗透数形结合的思想;
通过观察图象分析其性质,培养学生的探究、归纳及概括的能力.
重点
难点
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
一次函数图象
二次函数图象
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
反比例函数图象
描点法
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
x … -6 -4 -3 -2 -1 1 2 3 4 6 …
y … -1 -1.5 -2 -3 -6 6 3 2 1.5 1 …
画出反比例函数 的图象.
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
x … -6 -4 -3 -2 2 3 4 6 …
y … -2 -3 -4 -6 6 4 3 2 …
画出反比例函数 的图象.
双曲线
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
函数图象分别位于第一、三象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
在每一个象限内,y随x的增大而减小.
函数图象分别位于第一、三象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
k > 0
在每一个象限内,y随x的增大而减小.
函数图象分别位于第一、三象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
x … -6 -4 -3 -2 -1 1 2 3 4 6 …
y … 1 1.5 2 3 6 -6 -3 -2 -1.5 -1 …
画出反比例函数 的图象.
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
x … -6 -4 -3 -2 2 3 4 6 …
y … 2 3 4 6 -6 -4 -3 -2 …
画出反比例函数 的图象.
双曲线
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
性质
探究反比例函数 的性质.
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
函数图象分别位于第二、四象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质
性质
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究反比例函数 的性质.
性质
k < 0
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
反比例函数
性质
k < 0
在每一个象限内,y随x的增大而增大.
函数图象分别位于第二、四象限;
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
反比例函数
双曲线
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
观察思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
典型例题
例1.如图所示的图象对应的函数解析式为( )
A.
B.
C.
D.
D
双曲线
k<0
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.若双曲线 的图象的一支位于第三象限,
则m的取值范围是( )
A.
B.
C.
D.
B
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例3.已知双曲线 ,当x>0时,y随x的增大而增大,
则m的取值范围是 .
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例3.已知双曲线 ,当x>0时,y随x的增大而增大,
则m的取值范围是 .
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例3.已知双曲线 ,当x>0时,y随x的增大而增大,
则m的取值范围是 .
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
典型例题
随堂练习
练1.反比例函数 的图象位于( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
D
k=-4<0
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练2.下列反比例函数中,其图象的一个分支
一定在第三象限的是( )
(A)
(B)
(C)
(D)
(m为常数,且m≠-2)
(a为常数,且a≠±1)
C
k > 0
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练3.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数
的图象上,且x1
<
x1
x2
y1
y2
P1
P2
图象
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
随堂练习
反比例函数的图象和性质
性质
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
反比例函数的图象和性质
学习目标
反比例函数的图象和性质
进一步理解和掌握反比例函数的图象与性质;
灵活运用反比例函数的图象和性质解决问题;
领会反比例函数的解析式与图象的联系,体会数形结合与转化的思想方法;
体验数学活动中的探索性和创造性,感受数学美,激发学习兴趣.
重点
难点
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
反比例函数
双曲线
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
下列反比例函数:
想一想
(1)图象位于第一、三象限的是 ;
(2)图象位于第二、四象限的是 .
④
①
②
③
k > 0 函数图象分别位于一、三象限;
k < 0 函数图象分别位于二、四象限.
①
②
③
④
④
①
②
③
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
下列反比例函数:
想一想
(3)若0
④
①
②
③
④
①
②
③
k > 0 在每一个象限内,y随x的增大而减小;
k < 0 在每一个象限内,y随x的增大而增大.
①
③
②
④
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
下列反比例函数:
想一想
(3)若0
④
①
②
③
④
①
②
③
①
③
②
④
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
数形结合
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例1.已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于第几象限?y随x的增大如何变化?
y随x的变化情况与哪个量有关?
图象的位置由哪个量确定?
点在图象上意味着什么?
如何求这个量?
点A的坐标满足函数解析式
待定系数法
k > 0 函数图象分别位于一、三象限;
k < 0 函数图象分别位于二、四象限.
k > 0 在每一个象限内,y随x的增大而减小;
k < 0 在每一个象限内,y随x的增大而增大.
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例1.已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于第几象限?y随x的增大如何变化?
解:
设反比例函数的解析式为 ;
∵反比例函数的图象经过点A(2,6);
∴
,解得 ;
∴函数的图象分别位于第一、三象限,
在每个象限内,y随x的增大而减小.
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
解:
由(1)知反比例函数的解析式为 ;
分别将点B(3,4), ,D(2,5)代入;
当 时,
,所以点B在反比例函数的图象上;
当 时,
,所以点C在反比例函数的图象上;
当 时,
,所以点D不在反比例函数的图象上.
例1.已知反比例函数的图象经过点A(2,6).
(2)点B(3,4), ,D(2,5)是否在这个函数的图象上?
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
k > 0 函数图象分别位于一、三象限.
图象的另一支位于第三象限
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
解:(1)∵这个函数的图象的一支位于第一象限
∴另一支必位于第三象限
∵这个函数的图象位于第一、三象限
∴ ,即
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(2)在这个函数图象的某一支上任取点A(x1,y1)和点B(x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
k > 0 在每一个象限内,y随x的增大而减小.
x1
x2
y1
y2
A
B
y1
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
k > 0 在每一个象限内,y随x的增大而减小.
x1
x2
y1
y2
A
B
y1
根据图象,回答下列问题:
(2)在这个函数图象的某一支上任取点A(x1,y1)和点B(x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
巩固新知
课堂小结
布置作业
创设情境
应用新知
探究新知
典型例题
例2.如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(2)在这个函数图象的某一支上任取点A(x1,y1)和点B(x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
解:(2)∵
∴在这个函数图象的任一支上,
y随x的增大而减小
∴当 x1>x2时,y1
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练1.已知反比例的图象经过点A(1,-6).
(1)这个函数的图象位于第几象限?
在图象的每一支上,y随x的增大如何变化?
(2)点B(2,3),C(3,2), 是否在这个函数的图象上?
为什么?
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练1.已知反比例的图象经过点A(1,-6).
(1)这个函数的图象位于第几象限?
在图象的每一支上,y随x的增大如何变化?
解:
设反比例函数的解析式为 ;
∵反比例函数的图象经过点A(1,-6);
∴
,解得 ;
∴函数的图象分别位于第二、四象限,
在每个象限内,y随x的增大而增大.
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练1.已知反比例的图象经过点A(1,-6).
(2)点B(2,3),C(3,2), 是否在这个函数的图象上?
为什么?
解:
由(1)知反比例函数的解析式为 ;
分别将点B(2,-3),C(3,2), 代入;
当 时,
,所以点B在反比例函数的图象上;
当 时,
,所以点C不在反比例函数的图象上;
当 时,
,所以点D在反比例函数的图象上.
课堂小结
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练2.若点A(-2,a),B(-1,b),C(3,c)都在反比例函数
图象上,a,b,c有怎样的大小关系?
a
b
c
c
布置作业
创设情境
探究新知
随堂练习
应用新知
巩固新知
练2.若点A(-2,a),B(-1,b),C(3,c)都在反比例函数
图象上,a,b,c有怎样的大小关系?
解:
∵k < 0;
∴反比例函数的图象分别位于第二、四象限;
且在每个象限内,y随x的增大而增大;
∵-2 < -1 < 0 < 3;
∴c < 0 < a < b.
图象
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
随堂练习
反比例函数的图象和性质
性质
k < 0 函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
k > 0 函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
数形结合
