8.3.1 棱柱、棱锥、棱台的表面积和体积 课件(共21张PPT)
文档属性
| 名称 | 8.3.1 棱柱、棱锥、棱台的表面积和体积 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 08:25:26 | ||
图片预览





文档简介
(共21张PPT)
8.3.1 棱柱、棱锥、棱台的表面积和体积
第八章 立体几何初步
【学习目标】
1.通过对棱柱、棱锥、棱台的研究,掌握它们的表面积与体积的公式;
2.能解决实际问题中与多面体相关的简单几何体的表面积和体积;
3.通过学习感受一般化与特殊化、极限等数学思想方法,提高逻辑推理、直观想象等素养和空间想象等能力.
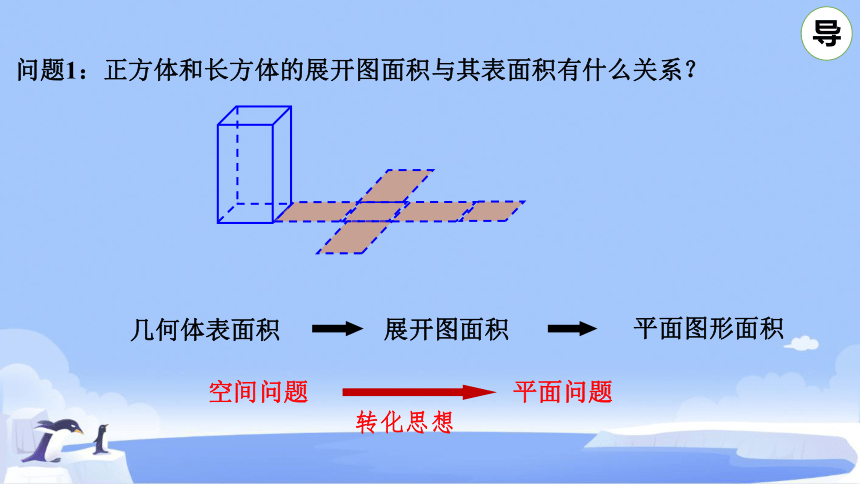
问题1:正方体和长方体的展开图面积与其表面积有什么关系?
几何体表面积
展开图面积
平面图形面积
空间问题
平面问题
转化思想
导
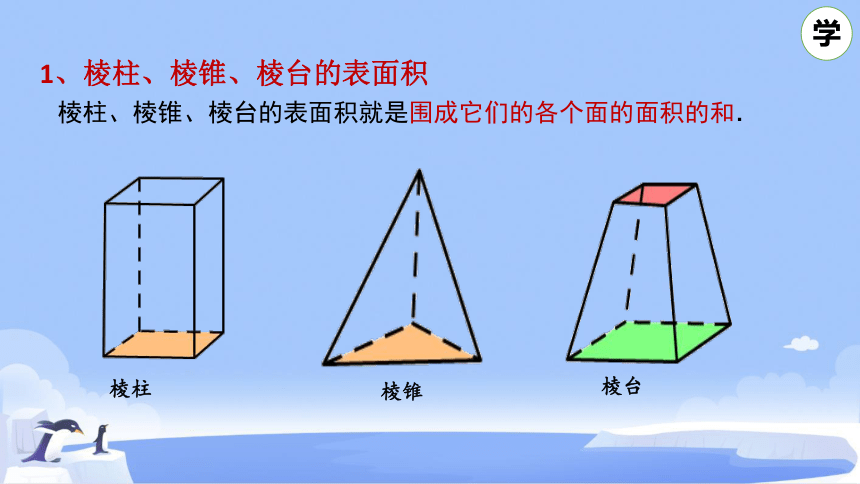
棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
棱柱
棱锥
棱台
学
1、棱柱、棱锥、棱台的表面积
例1 如图,四面体P-ABC各棱长均为a,求它的表面积.
解:∵ PBC是正三角形,其边长为a,
∴四面体P-ABC的表面积 .
∴
展
B
C
A
P
变式练习:正六棱台的上、下底面边长分别为2cm和6cm,侧棱长是5cm,求它的表面积.
展
解:如图所示,作 ,垂足为点H,
学
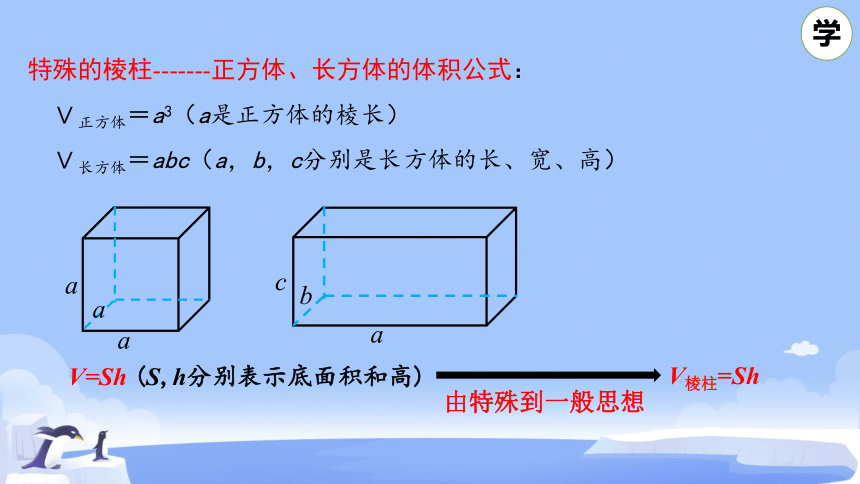
特殊的棱柱-------正方体、长方体的体积公式:
V正方体=a3(a是正方体的棱长)
V长方体=abc(a,b,c分别是长方体的长、宽、高)
V=Sh (S,h分别表示底面积和高)
由特殊到一般思想
V棱柱=Sh
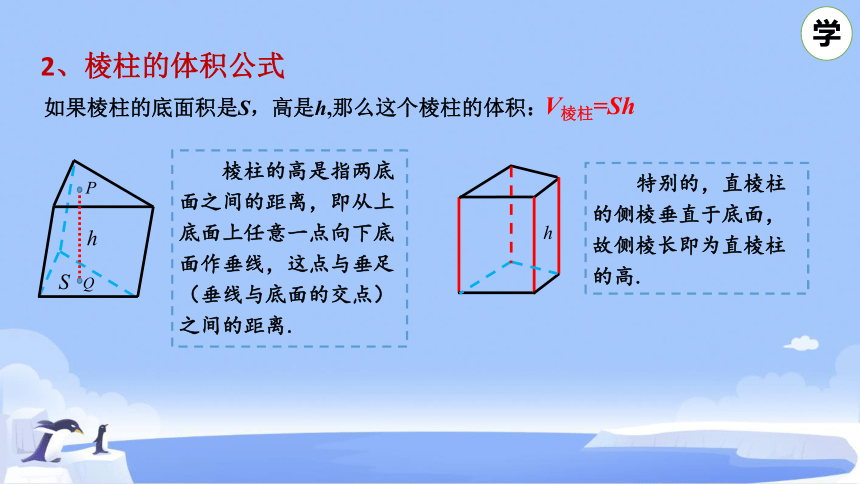
2、棱柱的体积公式
V棱柱=Sh
如果棱柱的底面积是S,高是h,那么这个棱柱的体积:
特别的,直棱柱的侧棱垂直于底面,故侧棱长即为直棱柱的高.
学
棱柱的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.
问题2: 取一摞书放在桌面上,并改变它的形状,高度、书中每页纸面积和顺序不变,观察改变前后的体积是否发生变化?
学
祖暅原理:
(456年~536年)
幂势既同,则积不容异.
夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
学
学
学
V=Sh
转化思想
等底等高
底面积和高都相等的棱柱,体积相等
V棱柱=Sh
问题3:棱锥与同底等高的棱柱体积之间有什么关系?
学
问题4:三个小棱锥的体积相等吗?
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.
学
3、棱锥的体积公式
棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
学
如果棱锥的底面面积为S,高为h,那么这个棱锥的体积:
V棱锥=Sh
4、棱台的体积公式
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
学
P
棱台的体积公式: ,(S′, S, h分别是棱台的上下底面积和高).
V棱台=(+)h
R
Q
问题5:观察棱柱、棱锥、棱台的体积公式之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
学
例2 如右图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01) (计算漏斗的容积时不考虑漏斗的厚度)
A'
B'
C'
D'
A
B
C
D
P
解:
如右下图,由题意知
V棱锥P-ABCD =
×1×1×0.5=
(m3),
所以这个漏斗的容积
V长方体ABCD-A'B'C'D' =1×1×0.5= (m3),
(m3).
练
课堂小结
评
多面体 图形 表面积 体积 思想方法
棱柱
棱锥 棱台 围成它们的各个面的面积的和
①转化思想
②由特殊到一般思想
③极限思想
(1)练习与巩固:固学案(46页)
(2)探究与发现:祖暅原理与棱柱、棱锥的体积(教材121页到122页)
学习需要巩固,理论要联系实际
谢谢!
8.3.1 棱柱、棱锥、棱台的表面积和体积
第八章 立体几何初步
【学习目标】
1.通过对棱柱、棱锥、棱台的研究,掌握它们的表面积与体积的公式;
2.能解决实际问题中与多面体相关的简单几何体的表面积和体积;
3.通过学习感受一般化与特殊化、极限等数学思想方法,提高逻辑推理、直观想象等素养和空间想象等能力.
问题1:正方体和长方体的展开图面积与其表面积有什么关系?
几何体表面积
展开图面积
平面图形面积
空间问题
平面问题
转化思想
导
棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
棱柱
棱锥
棱台
学
1、棱柱、棱锥、棱台的表面积
例1 如图,四面体P-ABC各棱长均为a,求它的表面积.
解:∵ PBC是正三角形,其边长为a,
∴四面体P-ABC的表面积 .
∴
展
B
C
A
P
变式练习:正六棱台的上、下底面边长分别为2cm和6cm,侧棱长是5cm,求它的表面积.
展
解:如图所示,作 ,垂足为点H,
学
特殊的棱柱-------正方体、长方体的体积公式:
V正方体=a3(a是正方体的棱长)
V长方体=abc(a,b,c分别是长方体的长、宽、高)
V=Sh (S,h分别表示底面积和高)
由特殊到一般思想
V棱柱=Sh
2、棱柱的体积公式
V棱柱=Sh
如果棱柱的底面积是S,高是h,那么这个棱柱的体积:
特别的,直棱柱的侧棱垂直于底面,故侧棱长即为直棱柱的高.
学
棱柱的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.
问题2: 取一摞书放在桌面上,并改变它的形状,高度、书中每页纸面积和顺序不变,观察改变前后的体积是否发生变化?
学
祖暅原理:
(456年~536年)
幂势既同,则积不容异.
夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
学
学
学
V=Sh
转化思想
等底等高
底面积和高都相等的棱柱,体积相等
V棱柱=Sh
问题3:棱锥与同底等高的棱柱体积之间有什么关系?
学
问题4:三个小棱锥的体积相等吗?
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.
学
3、棱锥的体积公式
棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
学
如果棱锥的底面面积为S,高为h,那么这个棱锥的体积:
V棱锥=Sh
4、棱台的体积公式
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
学
P
棱台的体积公式: ,(S′, S, h分别是棱台的上下底面积和高).
V棱台=(+)h
R
Q
问题5:观察棱柱、棱锥、棱台的体积公式之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
学
例2 如右图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01) (计算漏斗的容积时不考虑漏斗的厚度)
A'
B'
C'
D'
A
B
C
D
P
解:
如右下图,由题意知
V棱锥P-ABCD =
×1×1×0.5=
(m3),
所以这个漏斗的容积
V长方体ABCD-A'B'C'D' =1×1×0.5= (m3),
(m3).
练
课堂小结
评
多面体 图形 表面积 体积 思想方法
棱柱
棱锥 棱台 围成它们的各个面的面积的和
①转化思想
②由特殊到一般思想
③极限思想
(1)练习与巩固:固学案(46页)
(2)探究与发现:祖暅原理与棱柱、棱锥的体积(教材121页到122页)
学习需要巩固,理论要联系实际
谢谢!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
