18.1.2平行四边形的判定课件
文档属性
| 名称 | 18.1.2平行四边形的判定课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 315.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-26 00:00:00 | ||
图片预览


文档简介
课件24张PPT。18.1.2 平行四边形的判定
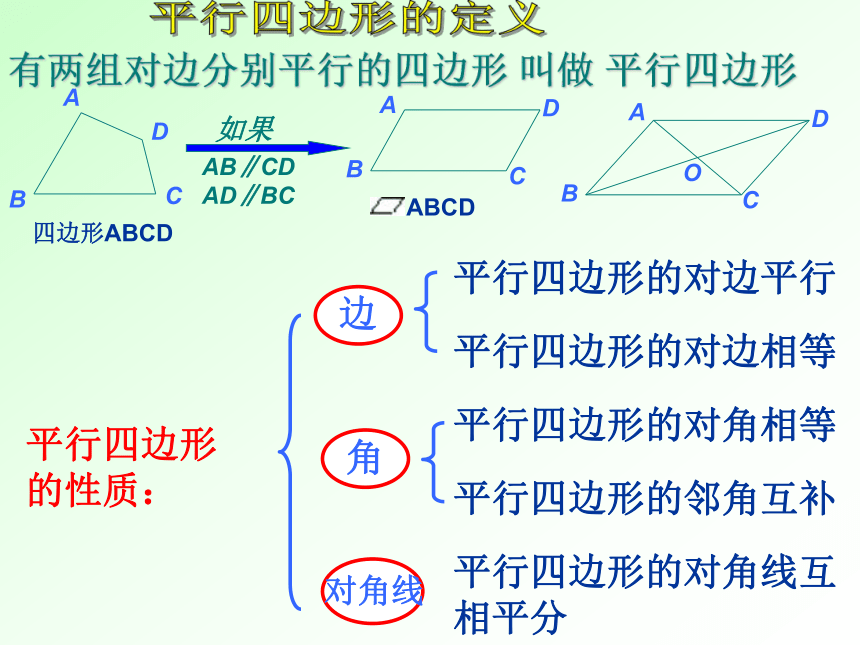
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
有两组对边分别平行的四边形叫做平行四边形平行四边形的定义平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分∵四边形ABCD 是平行四边形∴AB=CD
AD=BC∴AB∥CD
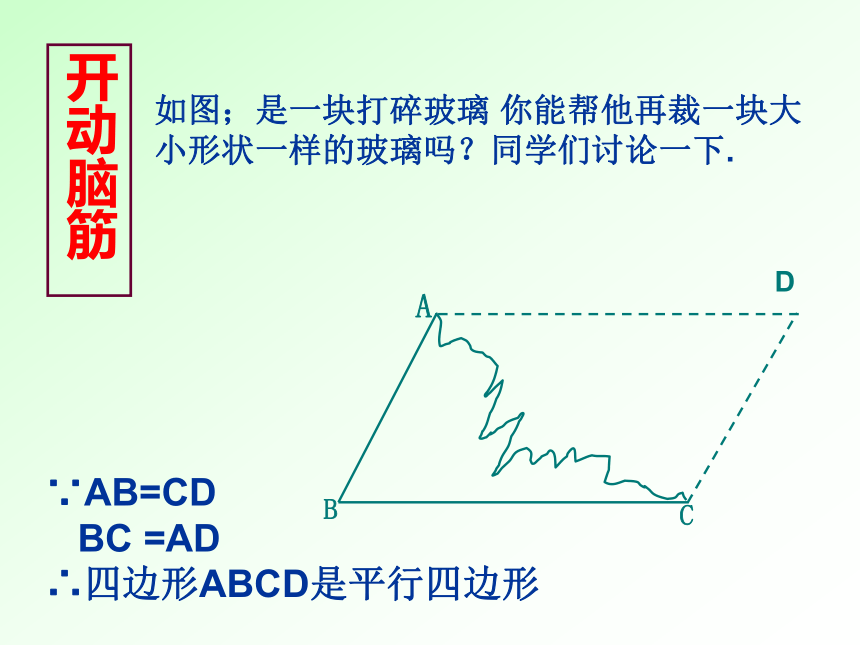
AD∥BC开动脑筋如图;是一块打碎玻璃 你能帮他再裁一块大小形状一样的玻璃吗?同学们讨论一下.
D∵AB=CD
BC =AD
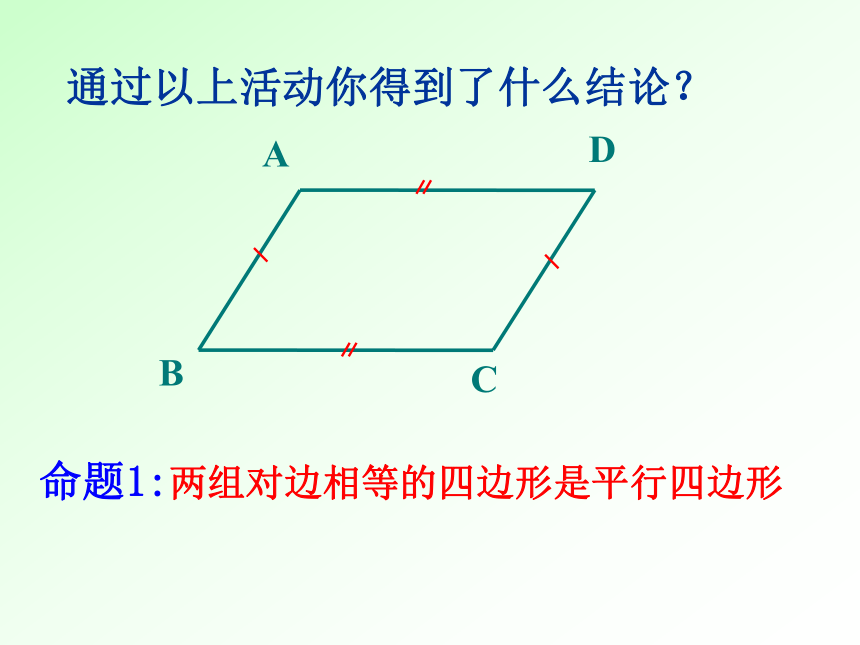
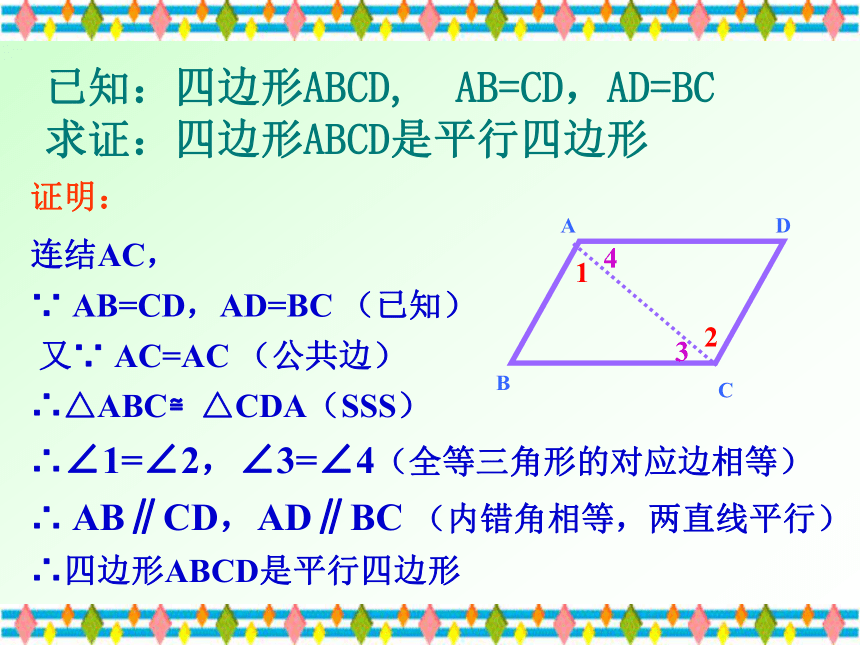
∴四边形ABCD是平行四边形通过以上活动你得到了什么结论? 命题1:两组对边相等的四边形是平行四边形BDAC已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形2134连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)证明:∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
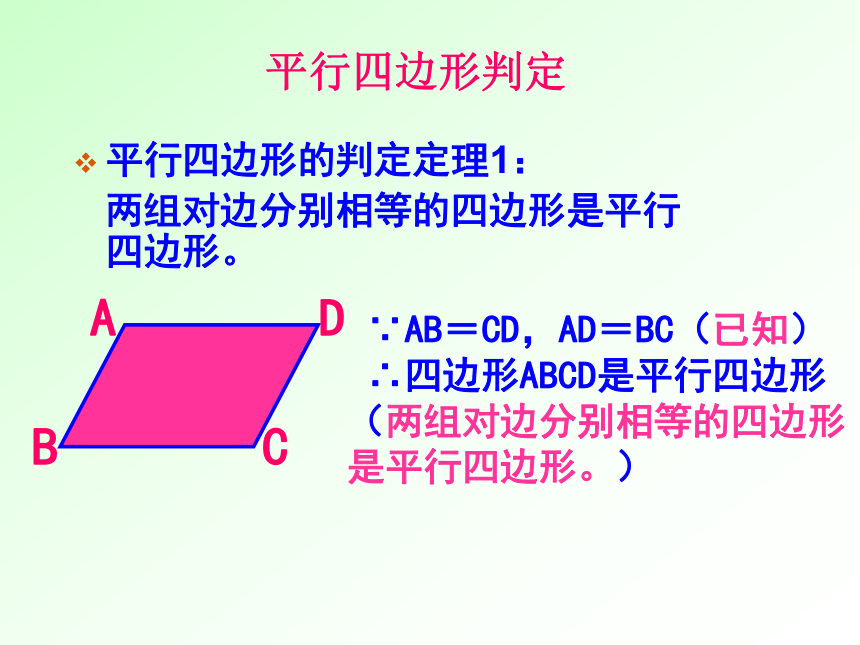
∴四边形ABCD是平行四边形平行四边形判定平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。 ∵AB=CD,AD=BC(已知)
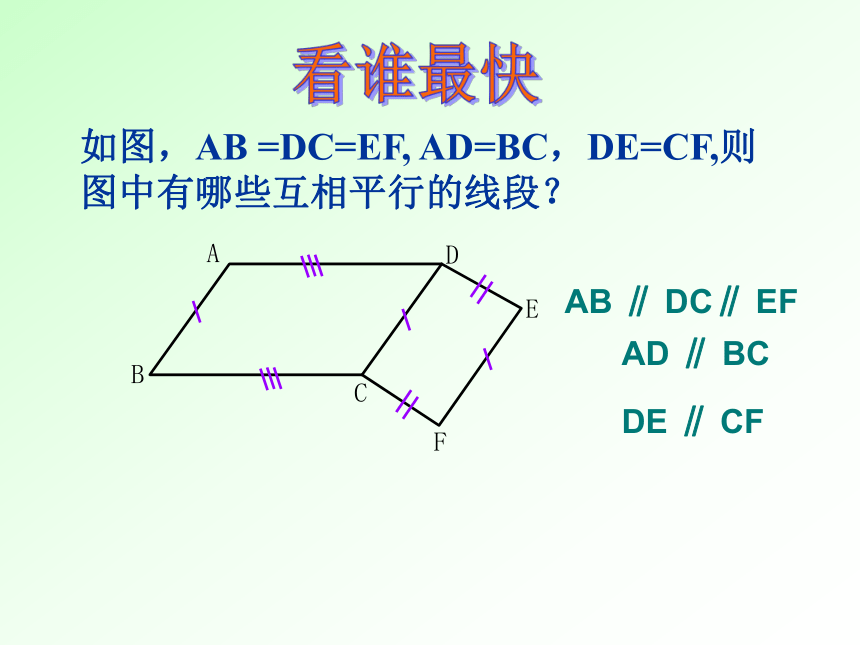
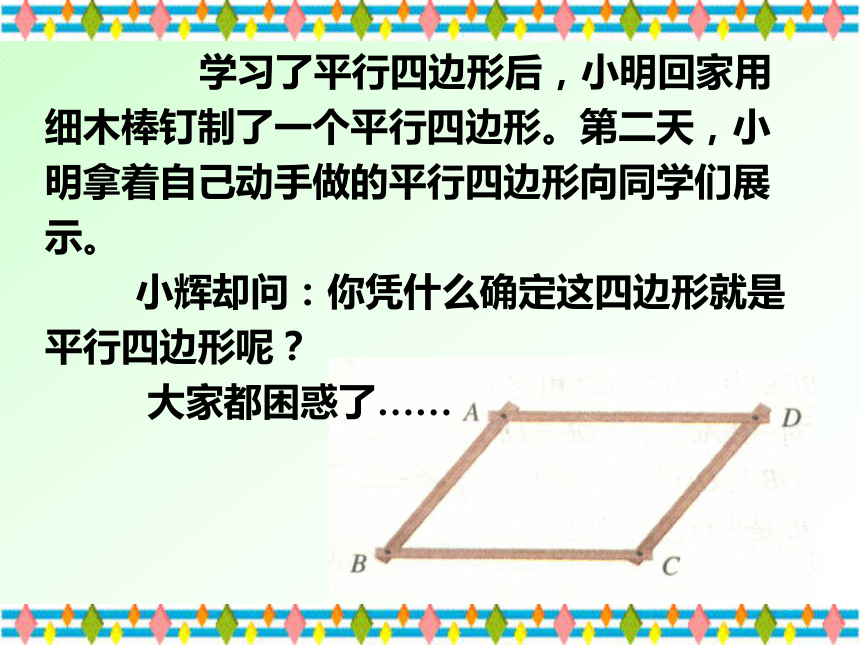
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形。) 如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF 学习了平行四边形后,小明回家用细木棒钉制了一个平行四边形。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……BDAC∠A+ ∠B=180 ° AD∥BC 小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形ABCD∠A+ ∠D=180 ° AB∥CD∠A+ ∠B +∠C+ ∠D =360 °BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °证明:即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形平行四边形的判定平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形。 ∵ ∠A=∠C,∠B=∠D (已知)
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形。) 小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认为小丽的做法有根据吗?已知:四边形ABCD中, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形试一试证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是
平行四边形)∴ ∠3 = ∠4已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
平行四边形的判定平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形。 ∵ OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形。) (1)根据定义:两组对边分别平行的四边
形叫做平行四边形。
(2)两组对边分别相等的四边形是平行
四边形。
(3)两组对角分别相等的四边形是平行四
边形。
(4)两条对角线互相平分的四边形是平
行四边形。平行四边形的判别方法开心一练:1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行C 请你识别下列四边形哪些是平行四边形?请说明理由?说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝大显身手练习1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ BO=DO
∴EO=FO
∴ 四边形BFDE是平行四边形
大显身手练习2:已知:E、F是平行四边形ABCD对角线AC上的两点,当点E,F满足什么条件时,四边形BFDE是平行四边形?DOABCEF体会.分享说出你这节课的收获和体验让大家与你分享吗?ABCD谢谢合作!再见
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
有两组对边分别平行的四边形叫做平行四边形平行四边形的定义平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分∵四边形ABCD 是平行四边形∴AB=CD
AD=BC∴AB∥CD
AD∥BC开动脑筋如图;是一块打碎玻璃 你能帮他再裁一块大小形状一样的玻璃吗?同学们讨论一下.
D∵AB=CD
BC =AD
∴四边形ABCD是平行四边形通过以上活动你得到了什么结论? 命题1:两组对边相等的四边形是平行四边形BDAC已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形2134连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)证明:∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形平行四边形判定平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。 ∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形。) 如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF 学习了平行四边形后,小明回家用细木棒钉制了一个平行四边形。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……BDAC∠A+ ∠B=180 ° AD∥BC 小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形ABCD∠A+ ∠D=180 ° AB∥CD∠A+ ∠B +∠C+ ∠D =360 °BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °证明:即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形平行四边形的判定平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形。 ∵ ∠A=∠C,∠B=∠D (已知)
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形。) 小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认为小丽的做法有根据吗?已知:四边形ABCD中, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形试一试证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是
平行四边形)∴ ∠3 = ∠4已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
平行四边形的判定平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形。 ∵ OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形。) (1)根据定义:两组对边分别平行的四边
形叫做平行四边形。
(2)两组对边分别相等的四边形是平行
四边形。
(3)两组对角分别相等的四边形是平行四
边形。
(4)两条对角线互相平分的四边形是平
行四边形。平行四边形的判别方法开心一练:1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行C 请你识别下列四边形哪些是平行四边形?请说明理由?说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝大显身手练习1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ BO=DO
∴EO=FO
∴ 四边形BFDE是平行四边形
大显身手练习2:已知:E、F是平行四边形ABCD对角线AC上的两点,当点E,F满足什么条件时,四边形BFDE是平行四边形?DOABCEF体会.分享说出你这节课的收获和体验让大家与你分享吗?ABCD谢谢合作!再见
