重庆市第八中学校2022-2023学年八年级(下)入学数学试卷(含答案)
文档属性
| 名称 | 重庆市第八中学校2022-2023学年八年级(下)入学数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 616.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 09:43:01 | ||
图片预览


文档简介
2022-2023学年重庆八中八年级(下)入学数学试卷
一、选择题。(本大题共10小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,请将答题卡上对应选项的方框涂黑.
1.(4分)2022年2月在北京和张家界举行了第24届冬季奥林匹克运动会,下列四个图案分别是四届冬奥会图标中的一部分,其中是轴对称图形的为( )
A. B.
C. D.
2.(4分)根据下列表述,不能确定一点的具体位置的是( )
A.东经122°,北纬43.6°
B.礼堂6排22号
C.重庆市宏帆路
D.港口南偏东60°方向上距港口10海里
3.(4分)下列因式分解正确的是( )
A.x2﹣xy+y2=(x﹣y)2
B.x2﹣5x﹣6=(x﹣2)(x﹣3)
C.x3﹣4x=x(x2﹣4)
D.9m2﹣4n2=(3m+2n)(3m﹣2n)
4.(4分)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
5.(4分)将点P(﹣2,6),先向右平移4个单位,再向下平移4个单位,则平移后得到点的坐标为( )
A.(2,2) B.(﹣2,﹣2) C.(﹣6,2) D.(﹣6,10)
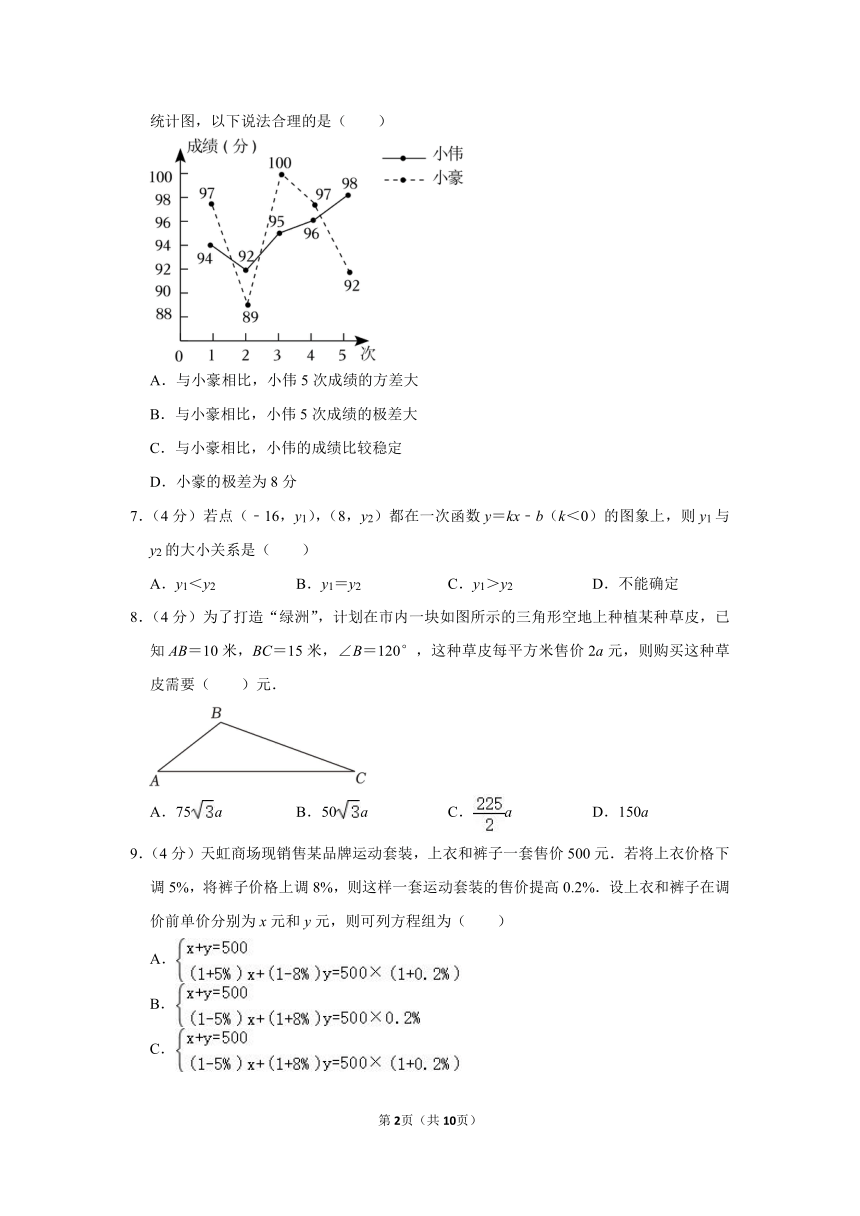
6.(4分)小豪和小伟积极参加学校组织的科普大赛,如图是根据5次预赛成绩绘制的折线统计图,以下说法合理的是( )
A.与小豪相比,小伟5次成绩的方差大
B.与小豪相比,小伟5次成绩的极差大
C.与小豪相比,小伟的成绩比较稳定
D.小豪的极差为8分
7.(4分)若点(﹣16,y1),(8,y2)都在一次函数y=kx﹣b(k<0)的图象上,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
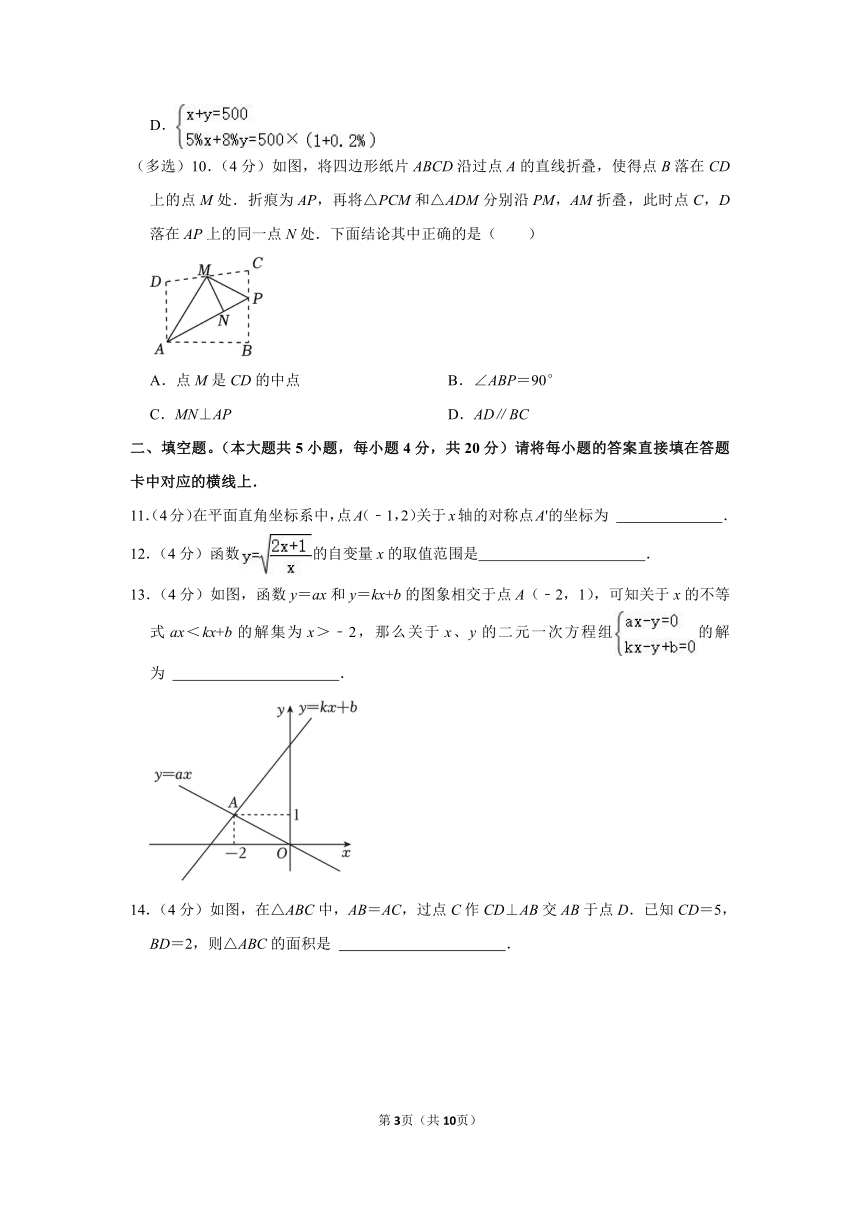
8.(4分)为了打造“绿洲”,计划在市内一块如图所示的三角形空地上种植某种草皮,已知AB=10米,BC=15米,∠B=120°,这种草皮每平方米售价2a元,则购买这种草皮需要( )元.
A.75a B.50a C.a D.150a
9.(4分)天虹商场现销售某品牌运动套装,上衣和裤子一套售价500元.若将上衣价格下调5%,将裤子价格上调8%,则这样一套运动套装的售价提高0.2%.设上衣和裤子在调价前单价分别为x元和y元,则可列方程组为( )
A.
B.
C.
D.
(多选)10.(4分)如图,将四边形纸片ABCD沿过点A的直线折叠,使得点B落在CD上的点M处.折痕为AP,再将△PCM和△ADM分别沿PM,AM折叠,此时点C,D落在AP上的同一点N处.下面结论其中正确的是( )
A.点M是CD的中点 B.∠ABP=90°
C.MN⊥AP D.AD∥BC
二、填空题。(本大题共5小题,每小题4分,共20分)请将每小题的答案直接填在答题卡中对应的横线上.
11.(4分)在平面直角坐标系中,点A(﹣1,2)关于x轴的对称点A'的坐标为 .
12.(4分)函数的自变量x的取值范围是 .
13.(4分)如图,函数y=ax和y=kx+b的图象相交于点A(﹣2,1),可知关于x的不等式ax<kx+b的解集为x>﹣2,那么关于x、y的二元一次方程组的解为 .
14.(4分)如图,在△ABC中,AB=AC,过点C作CD⊥AB交AB于点D.已知CD=5,BD=2,则△ABC的面积是 .
15.(4分)关于x、y的方程组与有相同的解,则(﹣a)b= .
三、解答题。(本大题共5小题,每题各8分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
16.(8分)解不等式组或化简计算.
(1);
(2).
17.(8分)因式分解.
(1)12mn﹣3n2;
(2)8a2﹣16ab+8b2.
18.(8分)为了加强安全教育,某校对学生进行“防溺水知识应知应答”测评.该校随机选取了八年级300名学生中的20名学生在10月份测评的成绩,数据如下:
收集数据:
97 91 89 95 90 99 90 97 91 98
90 90 91 88 98 97 95 90 96 88
整理、描述数据:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 a 3 2 1 3 2 1
数据分析:样本数据的平均数、众数、中位数和极差如表:
平均数 中位数 众数 极差
93 b c d
(1)a= ,b= ,c= ,d= ;
(2)该校决定授予在10月份测评成绩优秀(96分及以上)的八年级的学生“防溺水小卫士”荣誉称号,请估计评选该荣誉称号的人数.
(3)若被选取的20名学生在11月份测评的成绩的平均数、众数、中位数和极差如表:
平均数 中位数 众数 极差
95 93 94 10
结合相关数据,从一个方面评价10月份到11月份开展的“防溺水知识应知应答”测评活动的效果.
19.(8分)八年级(1)班张山同学利用所学函数知识,对函数y=|x+2|﹣x﹣1进行了如下研究:
列表如下:
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 …
Y … 7 5 3 m 1 n 1 1 1 …
描点并连线(如图)
(1)自变量x的取值范围是 ;
(2)表格中:m= ;n= ;
(3)在给出的坐标系中画出函数y=|x+2|﹣x﹣1的图象;
(4)一次函数y=﹣x+3的图象与函数y=|x+2|﹣x﹣1的图象交点的坐标为 .
20.(8分)在一款名为超级玛丽的游戏中.玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B.
(1)求旗杆的高度OM;
(2)求玛丽在荡绳索过程中离地面的最低点的高度MN.
四、选择题。(本大题共2小题,每小题4分,共8分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,请将答题卡上对应选项的方框涂黑.
21.(4分)如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于1,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )
A.4 B.5 C. D.
(多选)22.(4分)已知关于x的不等式组有且只有两个整数解,且一次函数y=kx+k﹣4的图象不经过第四象限,则下列四个数中符合条件的整数k值有( )
A.3 B.4 C.5 D.6
五、填空题。(本大题共3小题,每小题4分,共12分)请将每小题的答案直接填在答题卡中对应的横线上.
23.(4分)若直线y=kx+2与两坐标轴围成的三角形的面积是6个平方单位,则k= .
24.(4分)不论实数k取何值时,直线(k+1)x+(1﹣3k)y+2k﹣2=0恒过一定点,则该点的坐标是 .
25.(4分)甲、乙、丙、丁是四个不同平台的外卖员,每配送一单即可获得相应配送费且均为整数.已知乙每一单的配送费为甲的两倍,丁每一单的配送费为丙的两倍.12月第一周,甲、乙、丙的配送量之比为4:6:5,丁的配送量为100单,且他们共获得配送费3700元.第二周配送量增加,甲增加的配送量占乙、丙配送量之和的32%,丙增加的配送量占甲、乙、丙增加的配送量之和的,此时甲、乙的配送量之和为丙的配送量的倍,丁的配送量增加60单,且他们共获得配送费7660元.若丁每单配送费高于4元且不超过8元,则第二周四位外卖员配送量之和为 单.
六、解答题。(本大题共3小题,每题各10分,共30分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
26.(10分)已知一个四位自然数n.若n满足千位上的数字等于个位上的数字,百位上的数字等于十位和个位上的数字之和,则称n为“加油数”,对于一个“加油数”n,将n的百位数字记为x,百位数字与十位数字的积记为y,令F(n)=3x2﹣y.
例如:当n=1541时,∵1=1且5=4+1,∴1541是“加油数”;此时x=5,y=5×4=20,F(1541)=3×52﹣20=55;当n=3213时,∵3=3但2≠1+3,∴3213不是“加油数”.
(1)请判断2422,1531是否是“加油数”,并说明理由;如果是,请求出对应的F(n)的值;
(2)已知m是个位上的数字小于十位上的数字的“加油数”,将m的各个数位上的数字之和记为G(m),若能被4整除,求m的所有可能值.
27.(10分)如图,直线AD:y=kx+b过点A(1,3),D(2,4),直线DG⊥x轴于G点,点B与点A关于直线DG对称,直线AB与y轴交于点C,点F为y轴上一动点.
(1)求直线AD的解析式;
(2)点P为线段AD上一动点,过点P作AB的垂线段PH交AB于点H,当点P为线段AD的中点时,求的最小值及此时点F的坐标;
(3)在直线AD上是否存在一点P,使得以PF为直角边的△PBF为等腰直角三角形,若存在,直接写出所有点P的坐标及对应点F的坐标,若不存在,请说明理由.
28.(10分)已知,等腰直角△ABC中,AC=BC,∠ACB=90°,D为AB边上的一点,连接CD,以CD为斜边向右侧作直角△CDE,连接AE并延长交BC的延长线于点F.
(1)如图1,当∠CDE=30°,AD=1,BD=3时,求线段DE的长;
(2)如图2,当CE=DE时,求证:点E为线段AF的中点;
(3)如图3,点D与点A重合,AB=4,H为BF边上一点,G为AB边上一点,连接BE,当BE取最大值时,请直接写出三角形EHG周长的最小值.
2022-2023学年重庆八中八年级(下)入学数学试卷
参考答案
一、选择题。(本大题共10小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,请将答题卡上对应选项的方框涂黑.
1.C; 2.C; 3.D; 4.A; 5.A; 6.C; 7.C; 8.A; 9.C; 10.ABD;
二、填空题。(本大题共5小题,每小题4分,共20分)请将每小题的答案直接填在答题卡中对应的横线上.
11.(﹣1,﹣2); 12.x>0或x≤﹣; 13.; 14.; 15.﹣8;
三、解答题。(本大题共5小题,每题各8分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
16.(1)1<x≤2;
(2)﹣1.; 17.(1)3n(4m﹣n);(2)8(a﹣b)2.; 18.5; 91; 90; 11; 19.全体实数; 1; 1; (﹣6,9)和(2,1); 20.(1)旗杆的高度OM为15米;
(2)玛丽在荡绳索过程中离地面的最低点的高度MN为2米.;
四、选择题。(本大题共2小题,每小题4分,共8分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,请将答题卡上对应选项的方框涂黑.
21.B; 22.BC;
五、填空题。(本大题共3小题,每小题4分,共12分)请将每小题的答案直接填在答题卡中对应的横线上.
23.±; 24.(1,1); 25.1233;
六、解答题。(本大题共3小题,每题各10分,共30分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
26.(1)2422是“加油数”,F(2422)=3×42﹣8=40;1531不是“加油数”;
(2)1431,1871,2862,3853.; 27.(1)y=x+2;
(2),;
(3)在直线AD上存在一点P,使得以PF为直角边的△PBF为等腰直角三角形,;,F(0,5)或P(﹣1,1),F(0,4).; 28.(1);
(2)证明见解析过程;
(3).;
第1页(共1页)
一、选择题。(本大题共10小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,请将答题卡上对应选项的方框涂黑.
1.(4分)2022年2月在北京和张家界举行了第24届冬季奥林匹克运动会,下列四个图案分别是四届冬奥会图标中的一部分,其中是轴对称图形的为( )
A. B.
C. D.
2.(4分)根据下列表述,不能确定一点的具体位置的是( )
A.东经122°,北纬43.6°
B.礼堂6排22号
C.重庆市宏帆路
D.港口南偏东60°方向上距港口10海里
3.(4分)下列因式分解正确的是( )
A.x2﹣xy+y2=(x﹣y)2
B.x2﹣5x﹣6=(x﹣2)(x﹣3)
C.x3﹣4x=x(x2﹣4)
D.9m2﹣4n2=(3m+2n)(3m﹣2n)
4.(4分)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
5.(4分)将点P(﹣2,6),先向右平移4个单位,再向下平移4个单位,则平移后得到点的坐标为( )
A.(2,2) B.(﹣2,﹣2) C.(﹣6,2) D.(﹣6,10)
6.(4分)小豪和小伟积极参加学校组织的科普大赛,如图是根据5次预赛成绩绘制的折线统计图,以下说法合理的是( )
A.与小豪相比,小伟5次成绩的方差大
B.与小豪相比,小伟5次成绩的极差大
C.与小豪相比,小伟的成绩比较稳定
D.小豪的极差为8分
7.(4分)若点(﹣16,y1),(8,y2)都在一次函数y=kx﹣b(k<0)的图象上,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
8.(4分)为了打造“绿洲”,计划在市内一块如图所示的三角形空地上种植某种草皮,已知AB=10米,BC=15米,∠B=120°,这种草皮每平方米售价2a元,则购买这种草皮需要( )元.
A.75a B.50a C.a D.150a
9.(4分)天虹商场现销售某品牌运动套装,上衣和裤子一套售价500元.若将上衣价格下调5%,将裤子价格上调8%,则这样一套运动套装的售价提高0.2%.设上衣和裤子在调价前单价分别为x元和y元,则可列方程组为( )
A.
B.
C.
D.
(多选)10.(4分)如图,将四边形纸片ABCD沿过点A的直线折叠,使得点B落在CD上的点M处.折痕为AP,再将△PCM和△ADM分别沿PM,AM折叠,此时点C,D落在AP上的同一点N处.下面结论其中正确的是( )
A.点M是CD的中点 B.∠ABP=90°
C.MN⊥AP D.AD∥BC
二、填空题。(本大题共5小题,每小题4分,共20分)请将每小题的答案直接填在答题卡中对应的横线上.
11.(4分)在平面直角坐标系中,点A(﹣1,2)关于x轴的对称点A'的坐标为 .
12.(4分)函数的自变量x的取值范围是 .
13.(4分)如图,函数y=ax和y=kx+b的图象相交于点A(﹣2,1),可知关于x的不等式ax<kx+b的解集为x>﹣2,那么关于x、y的二元一次方程组的解为 .
14.(4分)如图,在△ABC中,AB=AC,过点C作CD⊥AB交AB于点D.已知CD=5,BD=2,则△ABC的面积是 .
15.(4分)关于x、y的方程组与有相同的解,则(﹣a)b= .
三、解答题。(本大题共5小题,每题各8分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
16.(8分)解不等式组或化简计算.
(1);
(2).
17.(8分)因式分解.
(1)12mn﹣3n2;
(2)8a2﹣16ab+8b2.
18.(8分)为了加强安全教育,某校对学生进行“防溺水知识应知应答”测评.该校随机选取了八年级300名学生中的20名学生在10月份测评的成绩,数据如下:
收集数据:
97 91 89 95 90 99 90 97 91 98
90 90 91 88 98 97 95 90 96 88
整理、描述数据:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 a 3 2 1 3 2 1
数据分析:样本数据的平均数、众数、中位数和极差如表:
平均数 中位数 众数 极差
93 b c d
(1)a= ,b= ,c= ,d= ;
(2)该校决定授予在10月份测评成绩优秀(96分及以上)的八年级的学生“防溺水小卫士”荣誉称号,请估计评选该荣誉称号的人数.
(3)若被选取的20名学生在11月份测评的成绩的平均数、众数、中位数和极差如表:
平均数 中位数 众数 极差
95 93 94 10
结合相关数据,从一个方面评价10月份到11月份开展的“防溺水知识应知应答”测评活动的效果.
19.(8分)八年级(1)班张山同学利用所学函数知识,对函数y=|x+2|﹣x﹣1进行了如下研究:
列表如下:
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 …
Y … 7 5 3 m 1 n 1 1 1 …
描点并连线(如图)
(1)自变量x的取值范围是 ;
(2)表格中:m= ;n= ;
(3)在给出的坐标系中画出函数y=|x+2|﹣x﹣1的图象;
(4)一次函数y=﹣x+3的图象与函数y=|x+2|﹣x﹣1的图象交点的坐标为 .
20.(8分)在一款名为超级玛丽的游戏中.玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B.
(1)求旗杆的高度OM;
(2)求玛丽在荡绳索过程中离地面的最低点的高度MN.
四、选择题。(本大题共2小题,每小题4分,共8分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,请将答题卡上对应选项的方框涂黑.
21.(4分)如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于1,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )
A.4 B.5 C. D.
(多选)22.(4分)已知关于x的不等式组有且只有两个整数解,且一次函数y=kx+k﹣4的图象不经过第四象限,则下列四个数中符合条件的整数k值有( )
A.3 B.4 C.5 D.6
五、填空题。(本大题共3小题,每小题4分,共12分)请将每小题的答案直接填在答题卡中对应的横线上.
23.(4分)若直线y=kx+2与两坐标轴围成的三角形的面积是6个平方单位,则k= .
24.(4分)不论实数k取何值时,直线(k+1)x+(1﹣3k)y+2k﹣2=0恒过一定点,则该点的坐标是 .
25.(4分)甲、乙、丙、丁是四个不同平台的外卖员,每配送一单即可获得相应配送费且均为整数.已知乙每一单的配送费为甲的两倍,丁每一单的配送费为丙的两倍.12月第一周,甲、乙、丙的配送量之比为4:6:5,丁的配送量为100单,且他们共获得配送费3700元.第二周配送量增加,甲增加的配送量占乙、丙配送量之和的32%,丙增加的配送量占甲、乙、丙增加的配送量之和的,此时甲、乙的配送量之和为丙的配送量的倍,丁的配送量增加60单,且他们共获得配送费7660元.若丁每单配送费高于4元且不超过8元,则第二周四位外卖员配送量之和为 单.
六、解答题。(本大题共3小题,每题各10分,共30分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
26.(10分)已知一个四位自然数n.若n满足千位上的数字等于个位上的数字,百位上的数字等于十位和个位上的数字之和,则称n为“加油数”,对于一个“加油数”n,将n的百位数字记为x,百位数字与十位数字的积记为y,令F(n)=3x2﹣y.
例如:当n=1541时,∵1=1且5=4+1,∴1541是“加油数”;此时x=5,y=5×4=20,F(1541)=3×52﹣20=55;当n=3213时,∵3=3但2≠1+3,∴3213不是“加油数”.
(1)请判断2422,1531是否是“加油数”,并说明理由;如果是,请求出对应的F(n)的值;
(2)已知m是个位上的数字小于十位上的数字的“加油数”,将m的各个数位上的数字之和记为G(m),若能被4整除,求m的所有可能值.
27.(10分)如图,直线AD:y=kx+b过点A(1,3),D(2,4),直线DG⊥x轴于G点,点B与点A关于直线DG对称,直线AB与y轴交于点C,点F为y轴上一动点.
(1)求直线AD的解析式;
(2)点P为线段AD上一动点,过点P作AB的垂线段PH交AB于点H,当点P为线段AD的中点时,求的最小值及此时点F的坐标;
(3)在直线AD上是否存在一点P,使得以PF为直角边的△PBF为等腰直角三角形,若存在,直接写出所有点P的坐标及对应点F的坐标,若不存在,请说明理由.
28.(10分)已知,等腰直角△ABC中,AC=BC,∠ACB=90°,D为AB边上的一点,连接CD,以CD为斜边向右侧作直角△CDE,连接AE并延长交BC的延长线于点F.
(1)如图1,当∠CDE=30°,AD=1,BD=3时,求线段DE的长;
(2)如图2,当CE=DE时,求证:点E为线段AF的中点;
(3)如图3,点D与点A重合,AB=4,H为BF边上一点,G为AB边上一点,连接BE,当BE取最大值时,请直接写出三角形EHG周长的最小值.
2022-2023学年重庆八中八年级(下)入学数学试卷
参考答案
一、选择题。(本大题共10小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,请将答题卡上对应选项的方框涂黑.
1.C; 2.C; 3.D; 4.A; 5.A; 6.C; 7.C; 8.A; 9.C; 10.ABD;
二、填空题。(本大题共5小题,每小题4分,共20分)请将每小题的答案直接填在答题卡中对应的横线上.
11.(﹣1,﹣2); 12.x>0或x≤﹣; 13.; 14.; 15.﹣8;
三、解答题。(本大题共5小题,每题各8分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
16.(1)1<x≤2;
(2)﹣1.; 17.(1)3n(4m﹣n);(2)8(a﹣b)2.; 18.5; 91; 90; 11; 19.全体实数; 1; 1; (﹣6,9)和(2,1); 20.(1)旗杆的高度OM为15米;
(2)玛丽在荡绳索过程中离地面的最低点的高度MN为2米.;
四、选择题。(本大题共2小题,每小题4分,共8分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,请将答题卡上对应选项的方框涂黑.
21.B; 22.BC;
五、填空题。(本大题共3小题,每小题4分,共12分)请将每小题的答案直接填在答题卡中对应的横线上.
23.±; 24.(1,1); 25.1233;
六、解答题。(本大题共3小题,每题各10分,共30分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
26.(1)2422是“加油数”,F(2422)=3×42﹣8=40;1531不是“加油数”;
(2)1431,1871,2862,3853.; 27.(1)y=x+2;
(2),;
(3)在直线AD上存在一点P,使得以PF为直角边的△PBF为等腰直角三角形,;,F(0,5)或P(﹣1,1),F(0,4).; 28.(1);
(2)证明见解析过程;
(3).;
第1页(共1页)
同课章节目录
