完全平方公式(安徽省芜湖市)
文档属性
| 名称 | 完全平方公式(安徽省芜湖市) |  | |
| 格式 | rar | ||
| 文件大小 | 32.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-26 18:05:00 | ||
图片预览


文档简介
课题:15.2.2完全平方公式
授 课 人:丁 芝 根
授课时间:2008年11月24日
授课地点:实验学校多媒体室
15.2.2 完全平方公式
教 学 任 务 分 析
学习目标 知识技能 1.掌握完全平方公式的推导及其应用。2.理解完全平方公式的几何解释。
数学思考 通过完全平方公式的推导及其应用的学习,培养思维的条理性和表达能力,增加符号感和推理能力。
解决问题 1.通过活动1,发现归纳并表达出完全平方公式。2.通过活动4,让学生自己发现问题,提出问题,然后解决问题,课外拓展资源,可继续深入学习。
情感态度 在灵活应用公式的过程中培养学习数学的兴趣,体验数形结合的思想和增强探索能力。
重点 完全平方公式的推导过程。
难点 理解完全平方公式的结构特征,并能灵活应用公式进行计算。
教 学 流 程 安 排
流程活动图 活动的内容和目的
活动1 探究完全平方公式 通过几个相近的式子提出问题,引出新知,探究新知,形成结论。
活动2 完全平方式的几何解释 通过动画演示,详细解析完全平方公式,进一步体验公式的特征。
活动3 理解和运用完全平方公式。 通过例题和习题的学习,认识完全平方公式的结构特征,并能进一步地运用解题。
活动4 巩固提高,拓展思维。 通过观察、思考、讨论、探究、拓展等环节,灵活运用所学知识。
活动5 小结作业 反思、自我评价、总结
教 学 过 程
问题与情境 师生行为 设计意图
活动1问题1:说说a2+b2与(a+b)2有什么区别?2:(a+b)2与(a-b)2的运算结果是否有规律?先找几个来试试:计算①(p+1)2=(p+1)(p+1)=___②(p-1)2=(p-1)(p-1)=____ ③(a+b)2=____④(a-b)2=_____用语言文字表达公式:两数和(或差)的平方等于这两数的平方和再加(或减)它们的积的2倍。 教学引导学生比较,学生口答。出示投影片后观察学生做题。然后引导学生发现(a+b)2与(a-b)2比较只有一次项有符号的差别。教学根据学生的叙述归纳出完全平方公式。板书公式(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2 或(a±b)2= a2±2ab+b2 本次活动中,教师关注: ①学生思考的积极性和演算的准确性。②学生语言表达的完整性。③教师的板书结构 通过对比复习引出新的知识点。通过4道小题的计算是对前面进行的运算的讨论,目的是让学生通过观察、归纳、鼓励学生发现这个公式的一些特点,如公式左右的特征,便于进一步应用公式计算。
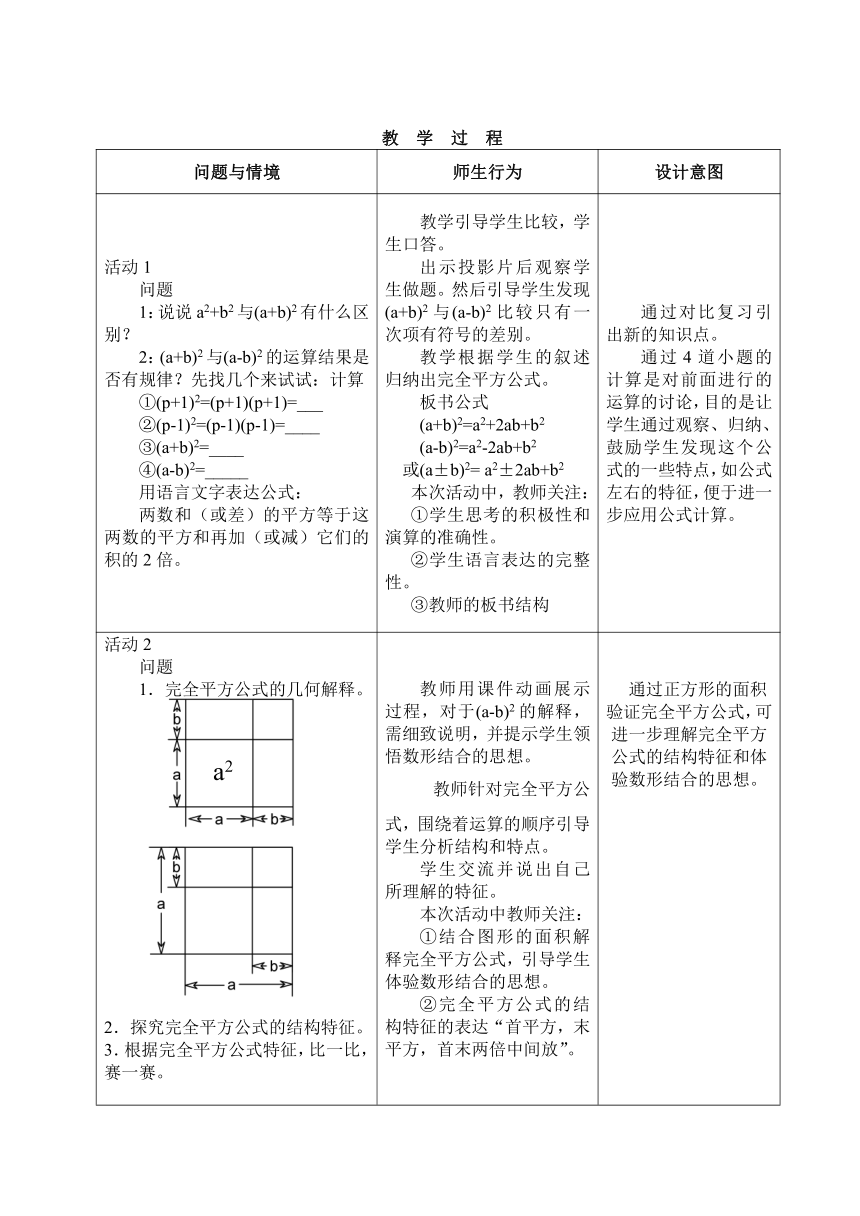
活动2问题1.完全平方公式的几何解释。2.探究完全平方公式的结构特征。3.根据完全平方公式特征,比一比,赛一赛。 教师用课件动画展示过程,对于(a-b)2的解释,需细致说明,并提示学生领悟数形结合的思想。教师针对完全平方公式,围绕着运算的顺序引导学生分析结构和特点。学生交流并说出自己所理解的特征。本次活动中教师关注:①结合图形的面积解释完全平方公式,引导学生体验数形结合的思想。②完全平方公式的结构特征的表达“首平方,末平方,首末两倍中间放”。 通过正方形的面积验证完全平方公式,可进一步理解完全平方公式的结构特征和体验数形结合的思想。
问题与情境 师生行为 设计意图
活动3例题精析例1 利用完全平方公式计算(1) (4m+n)2 ; (2) (y-0.5x)2 ; (3) (-a b)2 ; (4) (b-a)2问题1:比较(-a b)2与(a+b)2、(a-b)2与(b-a)2之间的关系如何?2:计算(1) (x +6)2 ; (2) (y -5)2; (3)(-2x+5)2; (4) 例2 运用完全平方公式计算(1) 1022 (2) 992问题计算 ①192 ②212 教师出示例题,并用课件展示具体的解题过程,引导学生结合完全平方公式的特点,去解题。学生观察、思考、理解。几个形式相近的式子比较容易混淆,引导学生辨析。学生上黑板解答,师生共同评析。学生运用完全平方公式,把数102,99化为两数和(或差)的形式。本次活动教师关注:①让学生学会规范地运用完全平方公式②将例题解决好后,应组织学生谈谈本次活动的感受,做好评价和反思。 通过例题和习题的教学过程,进一步巩固完全平方公式的应用,培养学生符号运算的能力,进一步培养学生的思维和表达能力。 在例2中通过灵活运用完全平方公式简化运算,增强学生的学以致用的意识。
活动4巩固提高,拓展思维一、判断题下列各式是否成立,说明理由。(1)(4a+1)2=(1 4a)2; ( ) (2) (4a 1)2=(4a+1)2; ( )(3)(4a 1)(1 4a)=(4a 1)(4a 1)=(4a 1)2; ( )(4)(4a 1)(1 4a)=(4a 1)(4a+1). ( ) 二、填空题(1)(-3x+4y)2=_________.(2)(-2a-b)2=_________.(3)x2-4xy+____=(x-2y)2.(4)a2+b2=(a+b)2+____.(5)a2+____+9b2=(a+3b)2 教师分发练习(另附页)引导学生共同完成部分习题。本次活动中,教师关注:①计算准确性、和灵活性。 进一步的综合应用,让学生更加熟练、准确,起到强化巩固的作用,初步发展学生综合运用的能力和灵活运用知识的能力。
问题与情境 师生行为 设计意图
三、选择题(1)如果x2+mx+4是一个完全平方公式,那么m的值是( ) A.4 B.-4 C.±4 D.±8(2)将正方形的边长由acm增加6cm,则正方形的面积增加了( )A.36cm2 B.12acm2C.(36+12a)cm2 D.以上都不对 ②完全平方公式的变式训练和效果。 对于思考题和拓展资源可让学生课下继续深入学习和研究,培养钻研好学的精神。
活动5小结作业:(1) 本节课你学到了什么知识?(2) 作业:见课本P156页习题15.2第2题。 学生小结,教师补充。学生独立完成,教师批改总结。本次活动中教师关注:①考察不同层次的学生对完全平方公式的掌握程度,应用针对性的分析与评价。②作业中学生出现问题的情况。 及时反思,便于学生将数学知识体系化,同时从能力、情感态度等方面关注学生对课堂的整体感受。及时了解学生用完全平方公解题的熟练性,准确性,便于调整教学安排。
教后反思:
附页:
一、判断题:下列各式是否成立,说明理由。
(1)(4a+1)2=(1 4a)2; ( )(2) (4a 1)2=(4a+1)2; ( )
(3)(4a 1)(1 4a)=(4a 1)(4a 1)=(4a 1)2; ( )
(4)(4a 1)(1 4a)=(4a 1)(4a+1). ( )
二、填空题
(1)(-3x+4y)2=_________. (2)(-2a-b)2=_________.
(3)x2-4xy+____=(x-2y)2. (4)a2+b2=(a+b)2+____.
(5)a2+____+9b2=(a+3b)2
三、选择题
(1)如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(2)将正方形的边长由acm增加6cm,则正方形的面积增加了( )
A.36cm2 B.12acm2 C.(36+12a)cm2 D.以上都不对
四、思考题:
已知:
五、拓展资源
①三种不同类型的矩形地砖长宽如图所示,若现有A类4块,B类4块,C类2块,要拼成一个正方形,则应多余出一块______型地砖,这样的地砖拼法表示了一个两数和的平方的几何意义,这个两数和的平方是________________
②试画出一个几何图形,使它的面积表示:
③利用下面两图分别计算:
(a+b+c)2=_______________________ (a+b)3=__________________________
④杨辉三角:
利用杨辉三角,你能求出(a+b)5吗?
芜湖县实验学校
县级开放周教学教案
a2
授 课 人:丁 芝 根
授课时间:2008年11月24日
授课地点:实验学校多媒体室
15.2.2 完全平方公式
教 学 任 务 分 析
学习目标 知识技能 1.掌握完全平方公式的推导及其应用。2.理解完全平方公式的几何解释。
数学思考 通过完全平方公式的推导及其应用的学习,培养思维的条理性和表达能力,增加符号感和推理能力。
解决问题 1.通过活动1,发现归纳并表达出完全平方公式。2.通过活动4,让学生自己发现问题,提出问题,然后解决问题,课外拓展资源,可继续深入学习。
情感态度 在灵活应用公式的过程中培养学习数学的兴趣,体验数形结合的思想和增强探索能力。
重点 完全平方公式的推导过程。
难点 理解完全平方公式的结构特征,并能灵活应用公式进行计算。
教 学 流 程 安 排
流程活动图 活动的内容和目的
活动1 探究完全平方公式 通过几个相近的式子提出问题,引出新知,探究新知,形成结论。
活动2 完全平方式的几何解释 通过动画演示,详细解析完全平方公式,进一步体验公式的特征。
活动3 理解和运用完全平方公式。 通过例题和习题的学习,认识完全平方公式的结构特征,并能进一步地运用解题。
活动4 巩固提高,拓展思维。 通过观察、思考、讨论、探究、拓展等环节,灵活运用所学知识。
活动5 小结作业 反思、自我评价、总结
教 学 过 程
问题与情境 师生行为 设计意图
活动1问题1:说说a2+b2与(a+b)2有什么区别?2:(a+b)2与(a-b)2的运算结果是否有规律?先找几个来试试:计算①(p+1)2=(p+1)(p+1)=___②(p-1)2=(p-1)(p-1)=____ ③(a+b)2=____④(a-b)2=_____用语言文字表达公式:两数和(或差)的平方等于这两数的平方和再加(或减)它们的积的2倍。 教学引导学生比较,学生口答。出示投影片后观察学生做题。然后引导学生发现(a+b)2与(a-b)2比较只有一次项有符号的差别。教学根据学生的叙述归纳出完全平方公式。板书公式(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2 或(a±b)2= a2±2ab+b2 本次活动中,教师关注: ①学生思考的积极性和演算的准确性。②学生语言表达的完整性。③教师的板书结构 通过对比复习引出新的知识点。通过4道小题的计算是对前面进行的运算的讨论,目的是让学生通过观察、归纳、鼓励学生发现这个公式的一些特点,如公式左右的特征,便于进一步应用公式计算。
活动2问题1.完全平方公式的几何解释。2.探究完全平方公式的结构特征。3.根据完全平方公式特征,比一比,赛一赛。 教师用课件动画展示过程,对于(a-b)2的解释,需细致说明,并提示学生领悟数形结合的思想。教师针对完全平方公式,围绕着运算的顺序引导学生分析结构和特点。学生交流并说出自己所理解的特征。本次活动中教师关注:①结合图形的面积解释完全平方公式,引导学生体验数形结合的思想。②完全平方公式的结构特征的表达“首平方,末平方,首末两倍中间放”。 通过正方形的面积验证完全平方公式,可进一步理解完全平方公式的结构特征和体验数形结合的思想。
问题与情境 师生行为 设计意图
活动3例题精析例1 利用完全平方公式计算(1) (4m+n)2 ; (2) (y-0.5x)2 ; (3) (-a b)2 ; (4) (b-a)2问题1:比较(-a b)2与(a+b)2、(a-b)2与(b-a)2之间的关系如何?2:计算(1) (x +6)2 ; (2) (y -5)2; (3)(-2x+5)2; (4) 例2 运用完全平方公式计算(1) 1022 (2) 992问题计算 ①192 ②212 教师出示例题,并用课件展示具体的解题过程,引导学生结合完全平方公式的特点,去解题。学生观察、思考、理解。几个形式相近的式子比较容易混淆,引导学生辨析。学生上黑板解答,师生共同评析。学生运用完全平方公式,把数102,99化为两数和(或差)的形式。本次活动教师关注:①让学生学会规范地运用完全平方公式②将例题解决好后,应组织学生谈谈本次活动的感受,做好评价和反思。 通过例题和习题的教学过程,进一步巩固完全平方公式的应用,培养学生符号运算的能力,进一步培养学生的思维和表达能力。 在例2中通过灵活运用完全平方公式简化运算,增强学生的学以致用的意识。
活动4巩固提高,拓展思维一、判断题下列各式是否成立,说明理由。(1)(4a+1)2=(1 4a)2; ( ) (2) (4a 1)2=(4a+1)2; ( )(3)(4a 1)(1 4a)=(4a 1)(4a 1)=(4a 1)2; ( )(4)(4a 1)(1 4a)=(4a 1)(4a+1). ( ) 二、填空题(1)(-3x+4y)2=_________.(2)(-2a-b)2=_________.(3)x2-4xy+____=(x-2y)2.(4)a2+b2=(a+b)2+____.(5)a2+____+9b2=(a+3b)2 教师分发练习(另附页)引导学生共同完成部分习题。本次活动中,教师关注:①计算准确性、和灵活性。 进一步的综合应用,让学生更加熟练、准确,起到强化巩固的作用,初步发展学生综合运用的能力和灵活运用知识的能力。
问题与情境 师生行为 设计意图
三、选择题(1)如果x2+mx+4是一个完全平方公式,那么m的值是( ) A.4 B.-4 C.±4 D.±8(2)将正方形的边长由acm增加6cm,则正方形的面积增加了( )A.36cm2 B.12acm2C.(36+12a)cm2 D.以上都不对 ②完全平方公式的变式训练和效果。 对于思考题和拓展资源可让学生课下继续深入学习和研究,培养钻研好学的精神。
活动5小结作业:(1) 本节课你学到了什么知识?(2) 作业:见课本P156页习题15.2第2题。 学生小结,教师补充。学生独立完成,教师批改总结。本次活动中教师关注:①考察不同层次的学生对完全平方公式的掌握程度,应用针对性的分析与评价。②作业中学生出现问题的情况。 及时反思,便于学生将数学知识体系化,同时从能力、情感态度等方面关注学生对课堂的整体感受。及时了解学生用完全平方公解题的熟练性,准确性,便于调整教学安排。
教后反思:
附页:
一、判断题:下列各式是否成立,说明理由。
(1)(4a+1)2=(1 4a)2; ( )(2) (4a 1)2=(4a+1)2; ( )
(3)(4a 1)(1 4a)=(4a 1)(4a 1)=(4a 1)2; ( )
(4)(4a 1)(1 4a)=(4a 1)(4a+1). ( )
二、填空题
(1)(-3x+4y)2=_________. (2)(-2a-b)2=_________.
(3)x2-4xy+____=(x-2y)2. (4)a2+b2=(a+b)2+____.
(5)a2+____+9b2=(a+3b)2
三、选择题
(1)如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(2)将正方形的边长由acm增加6cm,则正方形的面积增加了( )
A.36cm2 B.12acm2 C.(36+12a)cm2 D.以上都不对
四、思考题:
已知:
五、拓展资源
①三种不同类型的矩形地砖长宽如图所示,若现有A类4块,B类4块,C类2块,要拼成一个正方形,则应多余出一块______型地砖,这样的地砖拼法表示了一个两数和的平方的几何意义,这个两数和的平方是________________
②试画出一个几何图形,使它的面积表示:
③利用下面两图分别计算:
(a+b+c)2=_______________________ (a+b)3=__________________________
④杨辉三角:
利用杨辉三角,你能求出(a+b)5吗?
芜湖县实验学校
县级开放周教学教案
a2
