12.2 三角形全等的判定:边边边 课件(共31张PPT) 人教版数学八年级上册
文档属性
| 名称 | 12.2 三角形全等的判定:边边边 课件(共31张PPT) 人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
八年级数学
边边边
人教版
第十二章 全等三角形:三角形全等的判定
教学目标
构建三角形全等条件的探索思路,体会研究几何问题的方法.
探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等.
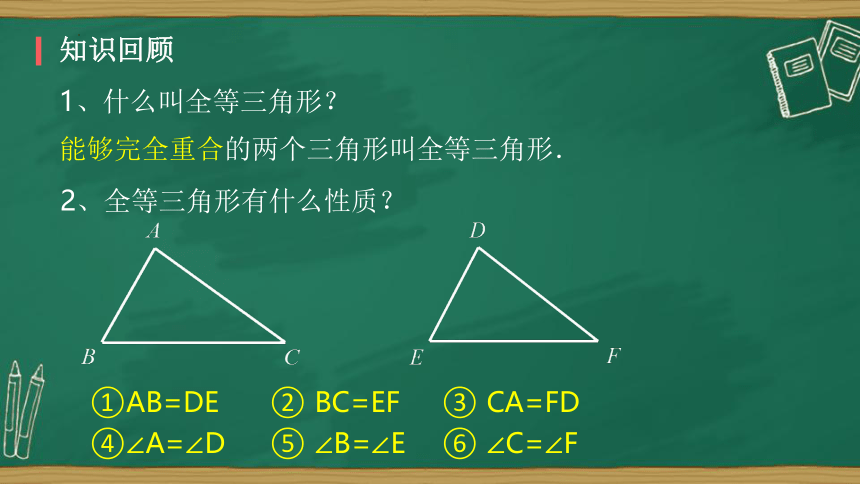
知识回顾
1、什么叫全等三角形?
能够完全重合的两个三角形叫全等三角形.
2、全等三角形有什么性质?
①AB=DE ② BC=EF ③ CA=FD
④∠A=∠D ⑤ ∠B=∠E ⑥ ∠C=∠F
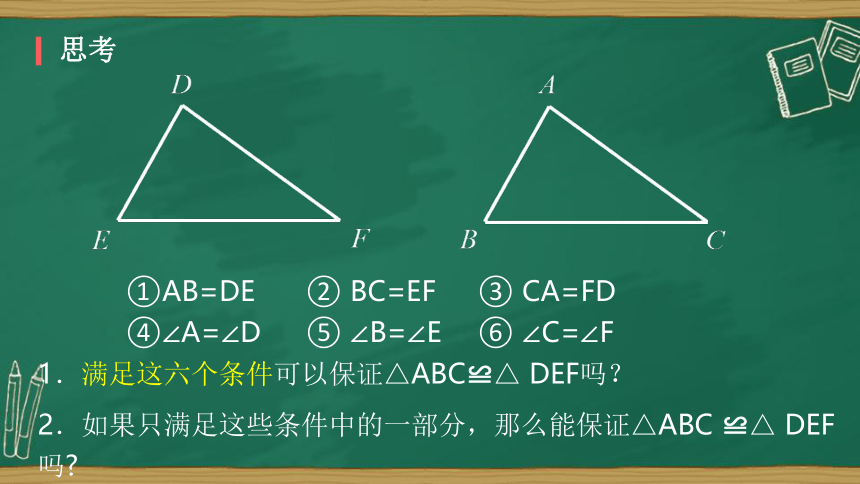
思考
①AB=DE ② BC=EF ③ CA=FD
④∠A=∠D ⑤ ∠B=∠E ⑥ ∠C=∠F
1.满足这六个条件可以保证△ABC≌△ DEF吗?
2.如果只满足这些条件中的一部分,那么能保证△ABC ≌△ DEF吗
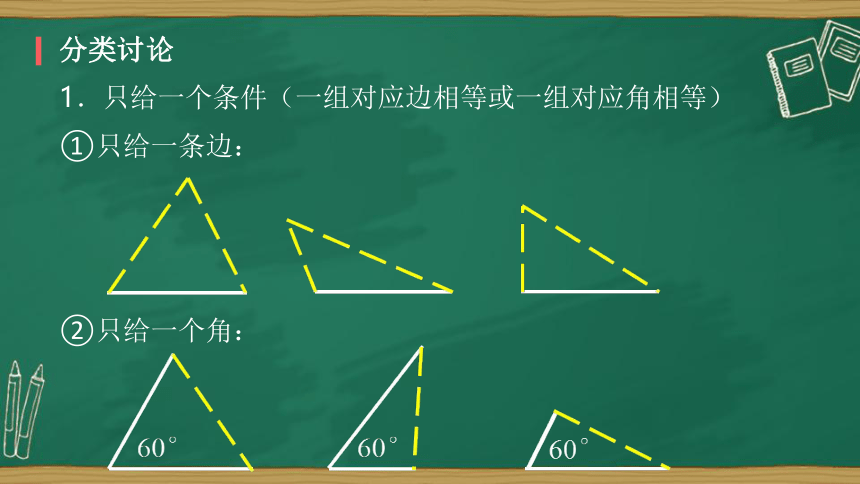
分类讨论
1.只给一个条件(一组对应边相等或一组对应角相等)
①只给一条边:
②只给一个角:
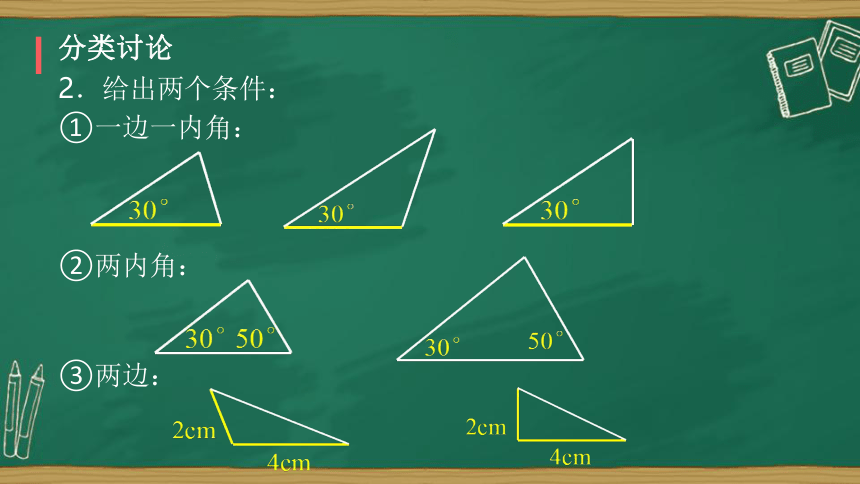
分类讨论
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
阶段性小结
一个条件
①一角;
②一边;
两个条件
①两角;
②两边;
③一边一角.
结论:只给出一个或两个条件时,
都不能保证所画的三角形一定全等.
分类讨论
3.给出三个条件,你能说出有哪几种可能的情况吗?
①三角;
②三边;
③两边一角;
④两角一边.
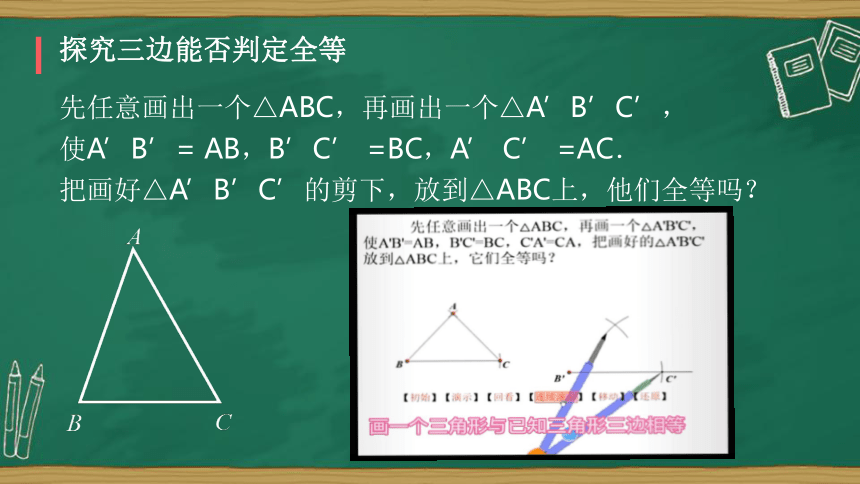
探究三角能否判定全等
举个例子:
已知两个三角形的三个内角分别为30°,60° ,90°,它们一定全等吗?
结论:三个角对应相等的两个三角形不一定全等
探究三边能否判定全等
先任意画出一个△ABC,再画出一个△A’B’C’,
使A’B’= AB,B’C’ =BC,A’ C’ =AC.
把画好△A’B’C’的剪下,放到△ABC上,他们全等吗?
探究三边能否判定全等
先任意画出一个△ABC,再画出一个△A’B’C’,
使A’B’= AB,B’C’ =BC,A’C’ =AC.
把画好△A’B’C’的剪下,放到△ABC上,他们全等吗?
画法:
(1)画线段B′C′=BC ;
(2)分别以B′、C′为圆心,BA、BC 为半径画弧,两弧交于点A′;
(3)连接线段A′B′,A’C’.
结论:全等
阶段性小结
已知三角对应相等,不能判定三角形全等.
已知三边对应相等,能判定三角形全等.
“两边一角”和“两角一边”呢?
以后再讨论
下面我们重点来学习“三边”的判定
边边边公理
三边对应相等的两个三角形全等简写为“边边边”或“SSS”
这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理.
“S ”就是Side
数学规范
如何书写三角形全等的证明过程呢?
在△ABC与△ 中
AB=
AC =
BC =
∴△ABC ≌△ (SSS)
书写的关键是要注意对应
A’
B’
C’
小试牛刀
如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
答案:有三组全等.△ABH ≌△ACH(SSS)
△ABD≌△ACD(SSS);△DBH ≌△DCH(SSS)
例题1
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC 中点D的支架.求证:△ ABD ≌△ ACD.
证明:∵D是BC 的中点
∴BD=CD
在△ABD与△ACD中
AB=AC
BD=CD
AD=AD
∴△ABD ≌△ACD(SSS)
书写时一定要注意对应
准备条件
指明范围
摆齐根据
写出结论
归纳总结
全等证明的书写步骤
①准备条件:把证全等时要用的条件先证好;
②三角形全等书写三步骤:
在△XXX与△XXX中
依次摆出
三组
等量关系
∴ △XXX ≌△XXX(SSS)
如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC.
例题2
提示:相等的边减去
公共边依然相等.
证明:∵BD=CE
∴BD-ED=CE-ED
∴BE=CD
在△AEB与△ADC中
AB=AC
AE=AD
BE=CD
∴△AEB ≌△ADC(SSS)
例题变式
已知如图AC=FE,BC=DE,点A,D,B,F在一条直线上,要用“边边边”证明△ABC≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?
答案:AB=FD或者AD=FB.
(相等的边加上公共边依旧相等)
练习4
如图,AB=CD,AC=BD,△ABC 和△DCB是否全等?试说明理由.
提示: 不要忘了公共边.
需要连公共边的问题
已知:如图,AB=AC,DB=DC,请说明∠B =∠C 成立的理由.
提示:连接AD.
需要连公共边的问题
已知:如图, 四边形ABCD中,AD=CB,AB=CD.
求证: ∠A= ∠C.
提示:连接BD.
练习5
已知:如图,AB = AC,AD = AE,BD = CE,BD 与 CE 交于点 O .求证:∠CAB=∠EAD.
提示:证明△ACE ≌△ABD.
总结
这节课我们学到了什么?
1.边边边公理:
有三边对应相等的两个三角形全等
简写成“边边边”(SSS)
2.全等证明的书写步骤
①准备条件:把证全等时要用的条件先证好;
②三角形全等书写三步骤:
在△XXX与△XXX中
依次摆出
三组
等量关系
∴ △XXX ≌△XXX(SSS)
总结
4 .学会了分类讨论和转化的数学思想。
3.边边边公理在应用中用到的数学方法:
证明线段或角相等
证明三角形全等
转化
认真听讲只能及格,用心思考才能优秀
练习
如图,已知AB=CD,AD=CB,E,F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
①△ADE ≌△CBF;②∠A=∠C.
提示:利用SSS 判定全等.
练习2
2.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合.过角尺顶点C 的射线OC便是∠AOB的平分线.为什么?
书写规范
如何书写三角形全等的证明过程呢?
在△ABC与△DEF 中
AB=DE
AC =DF
BC =EF
∴△ABC ≌△DEF(SSS)
书写的关键是要注意对应
练习1
1.如图,C是AB的中点,AD=CE,CD=BE.
求证△ACD ≌△CBE.
教学重点
构建三角形全等条件的探索思路,“边边边”判定方法.
教学难点
掌握利用“边边边”判定三角形全等技巧和过程书写要求.
八年级数学
边边边
人教版
第十二章 全等三角形:三角形全等的判定
教学目标
构建三角形全等条件的探索思路,体会研究几何问题的方法.
探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等.
知识回顾
1、什么叫全等三角形?
能够完全重合的两个三角形叫全等三角形.
2、全等三角形有什么性质?
①AB=DE ② BC=EF ③ CA=FD
④∠A=∠D ⑤ ∠B=∠E ⑥ ∠C=∠F
思考
①AB=DE ② BC=EF ③ CA=FD
④∠A=∠D ⑤ ∠B=∠E ⑥ ∠C=∠F
1.满足这六个条件可以保证△ABC≌△ DEF吗?
2.如果只满足这些条件中的一部分,那么能保证△ABC ≌△ DEF吗
分类讨论
1.只给一个条件(一组对应边相等或一组对应角相等)
①只给一条边:
②只给一个角:
分类讨论
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
阶段性小结
一个条件
①一角;
②一边;
两个条件
①两角;
②两边;
③一边一角.
结论:只给出一个或两个条件时,
都不能保证所画的三角形一定全等.
分类讨论
3.给出三个条件,你能说出有哪几种可能的情况吗?
①三角;
②三边;
③两边一角;
④两角一边.
探究三角能否判定全等
举个例子:
已知两个三角形的三个内角分别为30°,60° ,90°,它们一定全等吗?
结论:三个角对应相等的两个三角形不一定全等
探究三边能否判定全等
先任意画出一个△ABC,再画出一个△A’B’C’,
使A’B’= AB,B’C’ =BC,A’ C’ =AC.
把画好△A’B’C’的剪下,放到△ABC上,他们全等吗?
探究三边能否判定全等
先任意画出一个△ABC,再画出一个△A’B’C’,
使A’B’= AB,B’C’ =BC,A’C’ =AC.
把画好△A’B’C’的剪下,放到△ABC上,他们全等吗?
画法:
(1)画线段B′C′=BC ;
(2)分别以B′、C′为圆心,BA、BC 为半径画弧,两弧交于点A′;
(3)连接线段A′B′,A’C’.
结论:全等
阶段性小结
已知三角对应相等,不能判定三角形全等.
已知三边对应相等,能判定三角形全等.
“两边一角”和“两角一边”呢?
以后再讨论
下面我们重点来学习“三边”的判定
边边边公理
三边对应相等的两个三角形全等简写为“边边边”或“SSS”
这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理.
“S ”就是Side
数学规范
如何书写三角形全等的证明过程呢?
在△ABC与△ 中
AB=
AC =
BC =
∴△ABC ≌△ (SSS)
书写的关键是要注意对应
A’
B’
C’
小试牛刀
如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
答案:有三组全等.△ABH ≌△ACH(SSS)
△ABD≌△ACD(SSS);△DBH ≌△DCH(SSS)
例题1
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC 中点D的支架.求证:△ ABD ≌△ ACD.
证明:∵D是BC 的中点
∴BD=CD
在△ABD与△ACD中
AB=AC
BD=CD
AD=AD
∴△ABD ≌△ACD(SSS)
书写时一定要注意对应
准备条件
指明范围
摆齐根据
写出结论
归纳总结
全等证明的书写步骤
①准备条件:把证全等时要用的条件先证好;
②三角形全等书写三步骤:
在△XXX与△XXX中
依次摆出
三组
等量关系
∴ △XXX ≌△XXX(SSS)
如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC.
例题2
提示:相等的边减去
公共边依然相等.
证明:∵BD=CE
∴BD-ED=CE-ED
∴BE=CD
在△AEB与△ADC中
AB=AC
AE=AD
BE=CD
∴△AEB ≌△ADC(SSS)
例题变式
已知如图AC=FE,BC=DE,点A,D,B,F在一条直线上,要用“边边边”证明△ABC≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?
答案:AB=FD或者AD=FB.
(相等的边加上公共边依旧相等)
练习4
如图,AB=CD,AC=BD,△ABC 和△DCB是否全等?试说明理由.
提示: 不要忘了公共边.
需要连公共边的问题
已知:如图,AB=AC,DB=DC,请说明∠B =∠C 成立的理由.
提示:连接AD.
需要连公共边的问题
已知:如图, 四边形ABCD中,AD=CB,AB=CD.
求证: ∠A= ∠C.
提示:连接BD.
练习5
已知:如图,AB = AC,AD = AE,BD = CE,BD 与 CE 交于点 O .求证:∠CAB=∠EAD.
提示:证明△ACE ≌△ABD.
总结
这节课我们学到了什么?
1.边边边公理:
有三边对应相等的两个三角形全等
简写成“边边边”(SSS)
2.全等证明的书写步骤
①准备条件:把证全等时要用的条件先证好;
②三角形全等书写三步骤:
在△XXX与△XXX中
依次摆出
三组
等量关系
∴ △XXX ≌△XXX(SSS)
总结
4 .学会了分类讨论和转化的数学思想。
3.边边边公理在应用中用到的数学方法:
证明线段或角相等
证明三角形全等
转化
认真听讲只能及格,用心思考才能优秀
练习
如图,已知AB=CD,AD=CB,E,F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
①△ADE ≌△CBF;②∠A=∠C.
提示:利用SSS 判定全等.
练习2
2.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合.过角尺顶点C 的射线OC便是∠AOB的平分线.为什么?
书写规范
如何书写三角形全等的证明过程呢?
在△ABC与△DEF 中
AB=DE
AC =DF
BC =EF
∴△ABC ≌△DEF(SSS)
书写的关键是要注意对应
练习1
1.如图,C是AB的中点,AD=CE,CD=BE.
求证△ACD ≌△CBE.
教学重点
构建三角形全等条件的探索思路,“边边边”判定方法.
教学难点
掌握利用“边边边”判定三角形全等技巧和过程书写要求.
