切线的判定

课件14张PPT。《 切 线 的 判 定 》王 燕 华复习1、直线和圆有哪三种位置关系？这三种位置关 系是如何定义？如何判定的？ 设圆心到直线的距离为d,圆的半径为r。
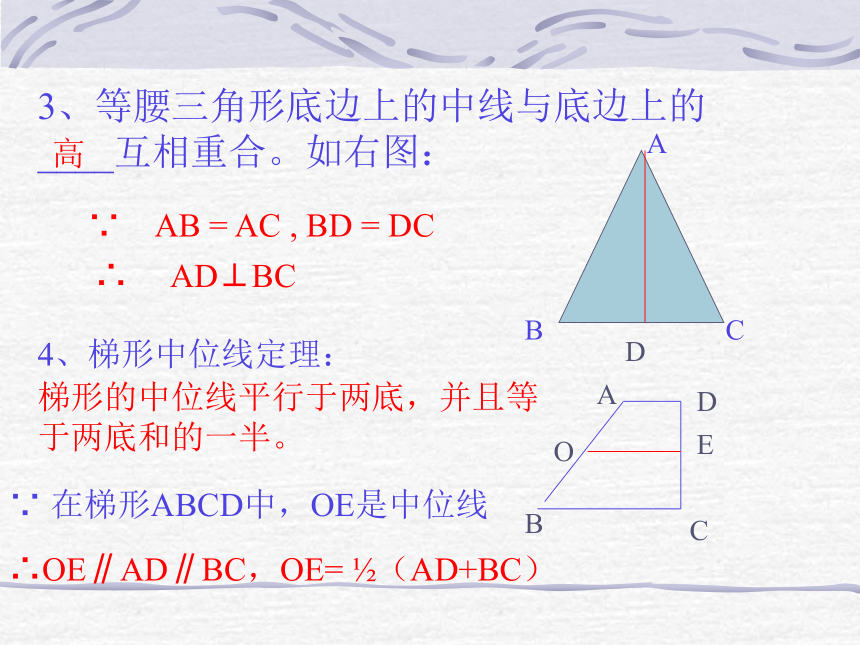
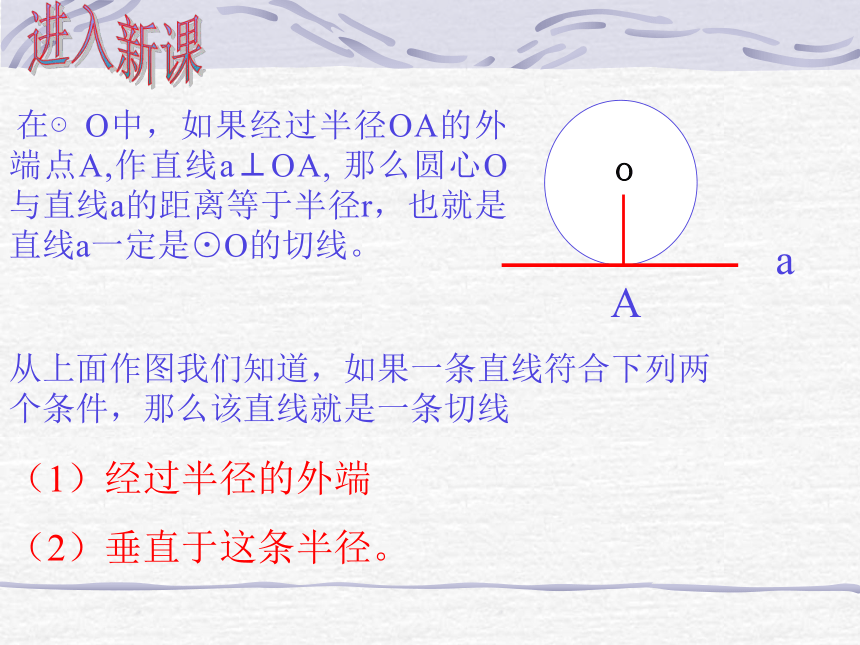
（1）直线与圆相离 d > r(2) 直线与圆相切 d = r（3）直线与圆相交 d < r2、什么叫切线？什么叫切点？ 3、等腰三角形底边上的中线与底边上的 ____互相重合。如右图：高ABCD∵　AB = AC , BD = DC∴ AD⊥BC4、梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半。ABCDOE∵ 在梯形ABCD中，OE是中位线∴OE∥AD∥BC，OE= ?（AD+BC）oa 在⊙O中，如果经过半径OA的外端点A,作直线a⊥OA, 那么圆心O与直线a的距离等于半径r，也就是直线a一定是⊙O的切线。 A 从上面作图我们知道，如果一条直线符合下列两个条件，那么该直线就是一条切线（1）经过半径的外端
（2）垂直于这条半径。
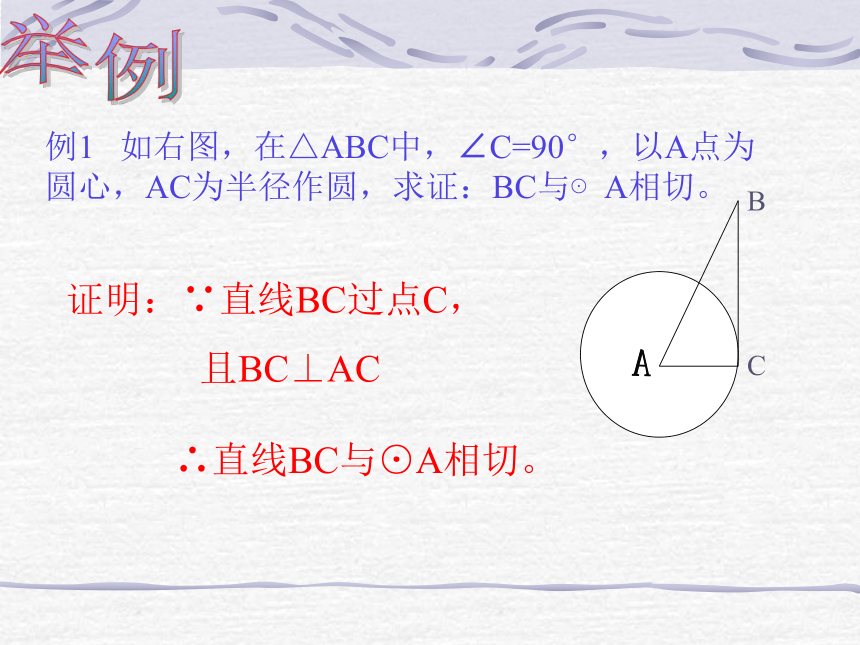
进入新课切线的判定定理 经过半径外端并且垂直于这条半径的直线是圆的切线。 请同学们思考一下，该判定定理的两个条件中缺少一个可以吗？ BAAB同学们讨论切线 的判定有哪些？1、利用切线的定义：与圆有唯一公共点的直线是圆的切线。 2、利用切线的判定定理：与圆心的距离等于半径的直 线是圆的切线。 3、利用切线的判定定理：经过半径外端并且垂直于半径的直线是圆的切线。 举例例1 如右图，在△ABC中，∠C=90°，以A点为圆心，AC为半径作圆，求证：BC与⊙A相切。 BC证明：∵直线BC过点C，
且BC⊥AC ∴直线BC与⊙A相切。 例2 已知：直线AB经过⊙O上的点C，并且OA=OB，
CA=CB
求证：直线AB是⊙O的切线。 ABC证明： 连结OC. ∵　 OA=OB, CA=CB, ∴　OC 是等腰三角形OAB底边AB上的中线。 ∴　AB⊥OC 直线AB经过半径OC的外端C，并且垂直于半径OC，所以AB是⊙O的切线。 ???例3、 已知：如下图，梯形ABCD中，AB∥CD，
∠A=90°，BC是⊙O的直径，BC=CD+AB。
求证：AD是⊙O的切线。 ABCDE 证明：作OE⊥AD于E，则
OE∥CD∥AB。 ∵OC=OB， ∴DE=EA。 ∴OE=1/2(AB+CD)=1/2BC =OC∴AD是⊙O的切线。 课堂练习?1、如图，AB是⊙O的直径，∠ABT=45°，AT=AB，
求证：AT是⊙O的切线。 ABT证明：∵　AT=AB∴ ∠ATB=∠ABT=45°∴　∠BTA=90°即：AT⊥OA直线AT经过半径OA的外端A，并且垂直于半径OA，所以AT是⊙O的切线。 ?2、 AB是⊙O的直径，点D在AB的延长线上，BD=OB， 点C在圆上，∠CAB=30°，
求证：DC是⊙O的切线。 OABDC证明：连结OC，BC∵ OA=OC ，∠CAB=30° ∴　∠BOC=60°∴　三角形OBC是等边三角形∴　BC=OB∵ BD=OB∴　BC=1/2OD∴△OCD是直角三角形即：DC⊥OC∴ DC是⊙O的切线小结
1、本节课主要学了切线的判定定理，该定理很重要，要求同学们牢牢掌握。
2、要求同学们掌握上述所讲的三种判定圆的切线的方法。 布置作业1、??? 阅读本节课的内容。
2、? 教科书中第115页第4题、第5题。
3、预习下节课内容。 再 见