人教版六年级下册数学圆柱的体积(课件)(共44张PPT)
文档属性
| 名称 | 人教版六年级下册数学圆柱的体积(课件)(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 11:45:17 | ||
图片预览






文档简介
(共44张PPT)
圆柱的体积
义务教育课程标准实验教科书(人教版)小学数学六年级下册
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
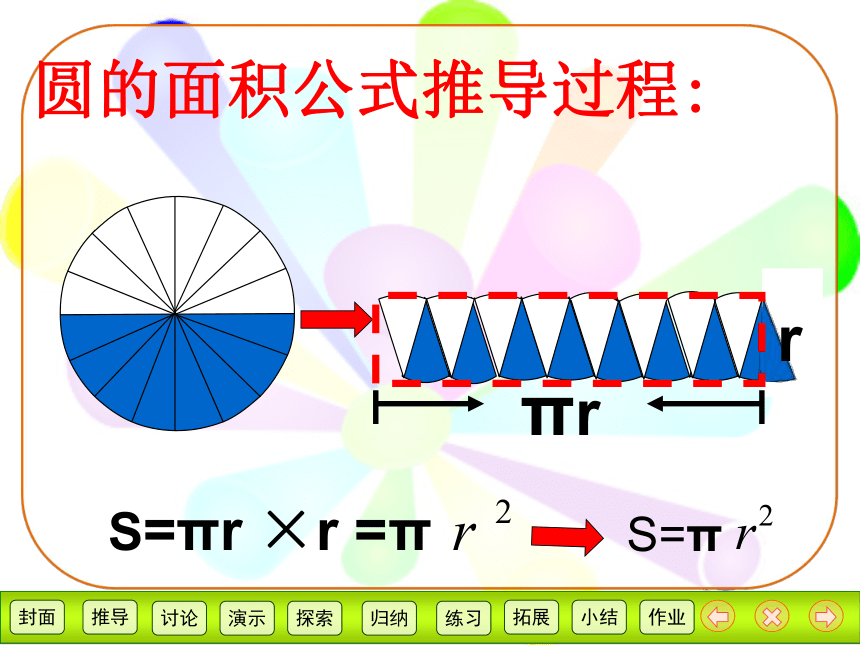
πr
r
S=πr ×r =π
S=π
圆的面积公式推导过程:
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
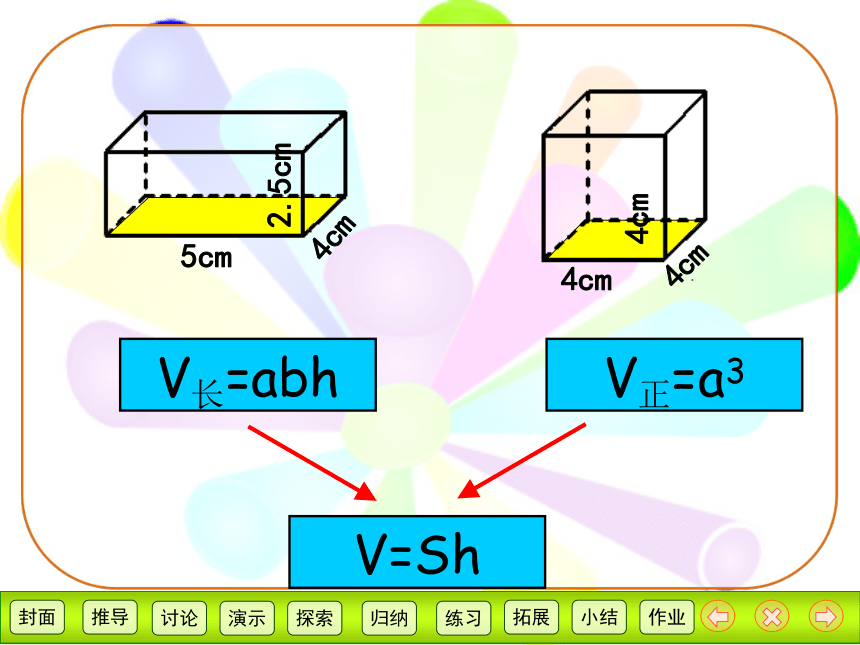
5cm
4cm
2.5cm
4cm
4cm
4cm
V长=abh
V正=a3
V=Sh
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
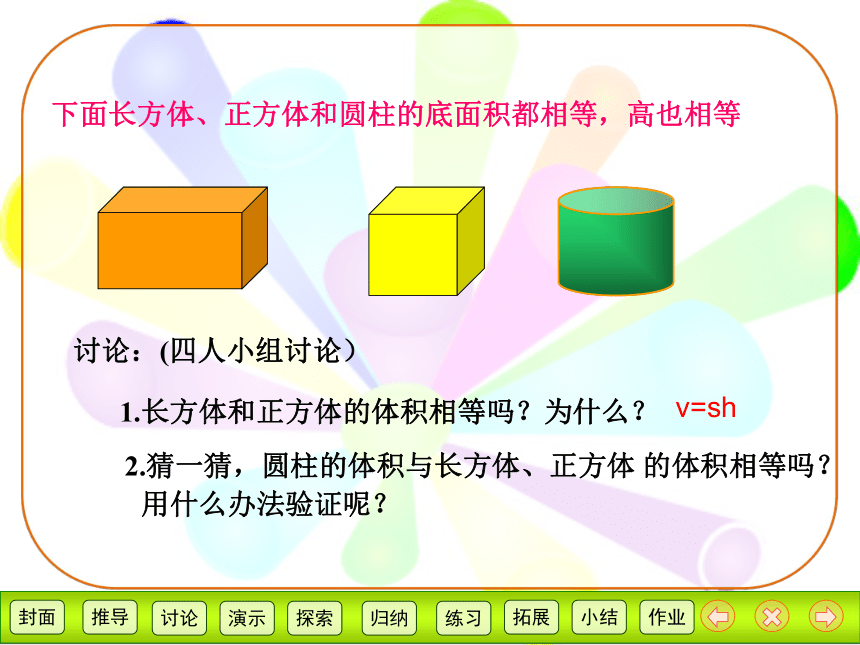
下面长方体、正方体和圆柱的底面积都相等,高也相等
讨论:(四人小组讨论)
1.长方体和正方体的体积相等吗?为什么?
2.猜一猜,圆柱的体积与长方体、正方体 的体积相等吗?
用什么办法验证呢?
v=sh
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
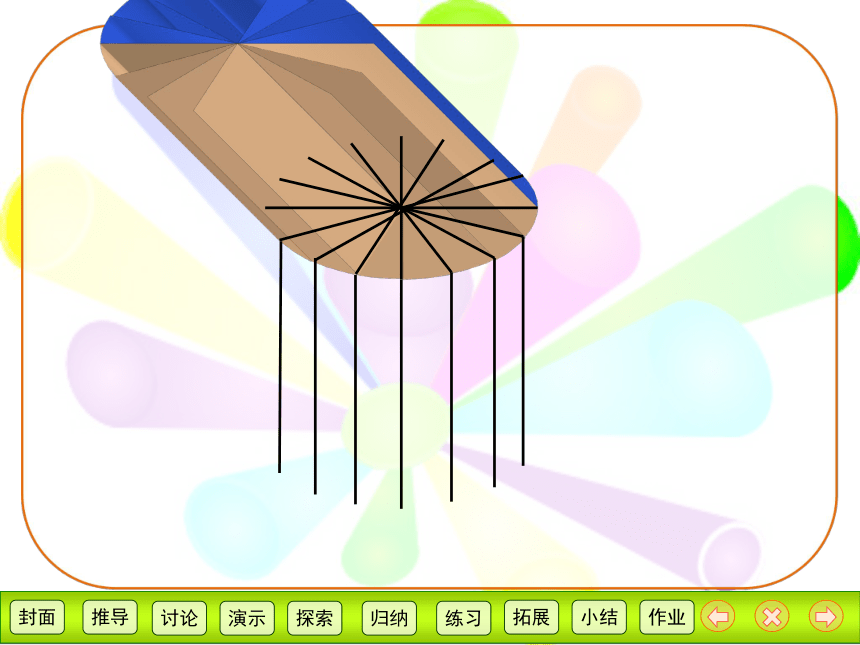
借助圆面积公式的推导方法,推导圆柱体积的计算公式。
1.学具拼一拼;2.观察拼成近似的长方体和原圆柱体的关系,回答讨论题:
1.拼成的近似的长方体的体积与原来的圆柱体体积是
否相等?
2.它的底面积变了吗?
3.它的高变了吗?
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
1.拼成近似的长方体的体积与原来的圆柱体体积是否相等?
2.它的底面积变了吗?
3.它的高变了吗?
实验与探索
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
长方体体积
圆柱体积
=
长方体的底面积
长方体的高
V圆柱=Sh
=底面积×高
=底面积×高
等于圆柱的底面积 ,
等于圆柱的高。
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
结论:
圆柱体通过切拼,圆柱体转化成近似的 体。这个长方体的底面积等于圆柱 的 ,高等于圆柱体的 。因为长方体的体积等于底面积乘上高,所以圆柱体的体积等于 用字母表示为 。
长方
底面积
高
底面积乘高
V=sh
V柱体=Sh
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
求圆柱体的体积必须知道哪些条件
底面积和高或底面半径和高。
怎样计算圆柱体的体积
已知底面积和高,
用公式V=Sh;
已知底面半径和高,
用公式V=πr2×h
如果已知直径,
先求半径,再用公式V=πr2×h
如果已知底面周长,
先求半径,r=C÷2÷π,再用公式V=πr2×h
圆柱的体积大小与什么有关?
底面半径或底面直径或底面积和高
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
小法官:
1.正方体、长方体、圆柱体的底面积和高相等,他们体积也相等。( )
2.长方体、正方体、圆柱体的体积都 可以用 底面积乘高的方法来计算。( )
3.圆柱体的底面积越大,它的 体积越大。( )
4.圆柱体的高越长,它的体积越大。( )
5.如果圆柱体的底面半径扩大2倍,高不变,体积也扩大2倍.( )
√
×
×
×
√
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
填空
1. 一个长方体和一个圆柱的体积相等,高
也相等,那么它们的底面积( )。
2.圆柱底面半径为r厘米,高为h厘米,
体积v=( )立方厘米
3.把一个圆柱切拼成一个近似的长方体,
长方体的底面积等于( ),
长方体高就是( )。
相等
πr2×h
圆柱的底面积
圆柱的高
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
一根圆柱形钢材,横截面的面积是50平方厘米,长是2米。它的体积是多少?
h=2米
s=50cm2
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
走进生活
一个圆柱形的电饭煲,从里面量得底面直径是2分
米,高是1.3分米。这个电饭煲的容积大约是多少 升?
(得数保留一位小数)
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
大厅里的柱子
底面周长是6.28米,高3.5米
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展延伸
把一根圆柱形木材横截成2段,表面积增加16平方厘米,它的
多少立方厘米?
底面积是多少平方厘米?如果这根木材长2.5米,它的体积是
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
1.谈一谈,这节课你有什么收获?还有哪些问题要问吗?
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
小结收获
计算——完成数学书21页练习三第1、2题。
运用——完成数学书21页练习三第4、5题。
实践——找出生活中的圆柱,测量出相关数据。并以《我学会了计算圆柱的体积》为题,写一篇数学日记。
(请任选一题做一做)
作业超市
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
圆柱的体积
义务教育课程标准实验教科书(人教版)小学数学六年级下册
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
πr
r
S=πr ×r =π
S=π
圆的面积公式推导过程:
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
5cm
4cm
2.5cm
4cm
4cm
4cm
V长=abh
V正=a3
V=Sh
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
下面长方体、正方体和圆柱的底面积都相等,高也相等
讨论:(四人小组讨论)
1.长方体和正方体的体积相等吗?为什么?
2.猜一猜,圆柱的体积与长方体、正方体 的体积相等吗?
用什么办法验证呢?
v=sh
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
借助圆面积公式的推导方法,推导圆柱体积的计算公式。
1.学具拼一拼;2.观察拼成近似的长方体和原圆柱体的关系,回答讨论题:
1.拼成的近似的长方体的体积与原来的圆柱体体积是
否相等?
2.它的底面积变了吗?
3.它的高变了吗?
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
1.拼成近似的长方体的体积与原来的圆柱体体积是否相等?
2.它的底面积变了吗?
3.它的高变了吗?
实验与探索
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
长方体体积
圆柱体积
=
长方体的底面积
长方体的高
V圆柱=Sh
=底面积×高
=底面积×高
等于圆柱的底面积 ,
等于圆柱的高。
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
结论:
圆柱体通过切拼,圆柱体转化成近似的 体。这个长方体的底面积等于圆柱 的 ,高等于圆柱体的 。因为长方体的体积等于底面积乘上高,所以圆柱体的体积等于 用字母表示为 。
长方
底面积
高
底面积乘高
V=sh
V柱体=Sh
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
求圆柱体的体积必须知道哪些条件
底面积和高或底面半径和高。
怎样计算圆柱体的体积
已知底面积和高,
用公式V=Sh;
已知底面半径和高,
用公式V=πr2×h
如果已知直径,
先求半径,再用公式V=πr2×h
如果已知底面周长,
先求半径,r=C÷2÷π,再用公式V=πr2×h
圆柱的体积大小与什么有关?
底面半径或底面直径或底面积和高
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
小法官:
1.正方体、长方体、圆柱体的底面积和高相等,他们体积也相等。( )
2.长方体、正方体、圆柱体的体积都 可以用 底面积乘高的方法来计算。( )
3.圆柱体的底面积越大,它的 体积越大。( )
4.圆柱体的高越长,它的体积越大。( )
5.如果圆柱体的底面半径扩大2倍,高不变,体积也扩大2倍.( )
√
×
×
×
√
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
填空
1. 一个长方体和一个圆柱的体积相等,高
也相等,那么它们的底面积( )。
2.圆柱底面半径为r厘米,高为h厘米,
体积v=( )立方厘米
3.把一个圆柱切拼成一个近似的长方体,
长方体的底面积等于( ),
长方体高就是( )。
相等
πr2×h
圆柱的底面积
圆柱的高
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
一根圆柱形钢材,横截面的面积是50平方厘米,长是2米。它的体积是多少?
h=2米
s=50cm2
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
走进生活
一个圆柱形的电饭煲,从里面量得底面直径是2分
米,高是1.3分米。这个电饭煲的容积大约是多少 升?
(得数保留一位小数)
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
大厅里的柱子
底面周长是6.28米,高3.5米
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展延伸
把一根圆柱形木材横截成2段,表面积增加16平方厘米,它的
多少立方厘米?
底面积是多少平方厘米?如果这根木材长2.5米,它的体积是
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
1.谈一谈,这节课你有什么收获?还有哪些问题要问吗?
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
小结收获
计算——完成数学书21页练习三第1、2题。
运用——完成数学书21页练习三第4、5题。
实践——找出生活中的圆柱,测量出相关数据。并以《我学会了计算圆柱的体积》为题,写一篇数学日记。
(请任选一题做一做)
作业超市
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
拓展
练习
归纳
探索
演示
讨论
推导
封面
小结
作业
