18.2.3正方形 正方形的判定 课件(共32张PPT) 人教版数学八年级下册
文档属性
| 名称 | 18.2.3正方形 正方形的判定 课件(共32张PPT) 人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 910.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 00:00:00 | ||
图片预览




文档简介
(共32张PPT)
正方形的判定
第十八章 平行四边形
正方形的自我介绍:在四边形的大家庭中,我有四个兄弟.
老大是平行四边形,它性格温和;老二是矩形,它稳重大方,江湖上人称长方形;老三是菱形,它活泼可爱.我就是正方形老四,我集三位大哥的优点于一身,人见人爱.
回顾导入
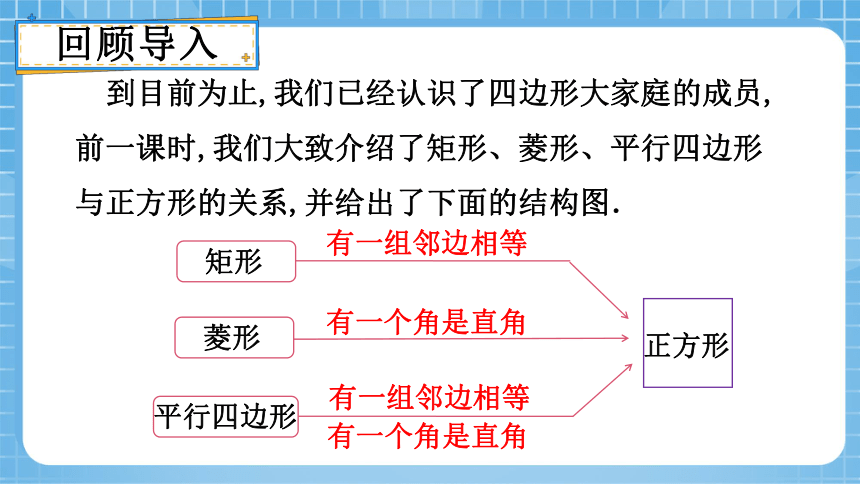
到目前为止,我们已经认识了四边形大家庭的成员,前一课时,我们大致介绍了矩形、菱形、平行四边形与正方形的关系,并给出了下面的结构图.
回顾导入
平行四边形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
正方形
可以看到矩形、菱形各添加一个条件都能得到正方形,那么这个是否可以证明呢 我们这节课来看下.
回顾导入
平行四边形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
正方形
我们来看下面这个问题:
正方形的判定
探究点
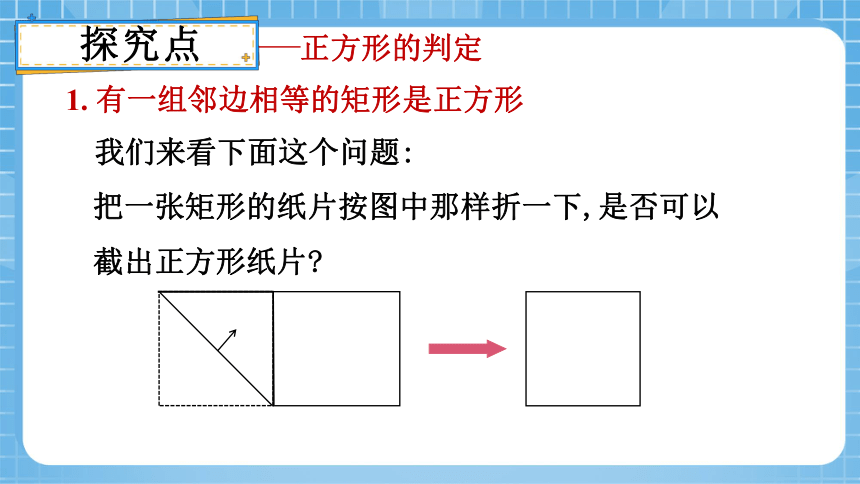
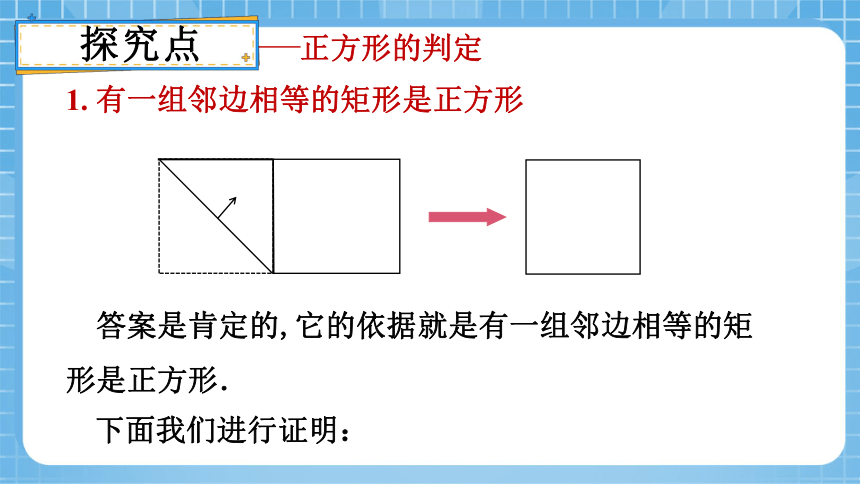
1. 有一组邻边相等的矩形是正方形
把一张矩形的纸片按图中那样折一下,是否可以截出正方形纸片
正方形的判定
探究点
1. 有一组邻边相等的矩形是正方形
答案是肯定的,它的依据就是有一组邻边相等的矩形是正方形.
下面我们进行证明:
A
D
B
C
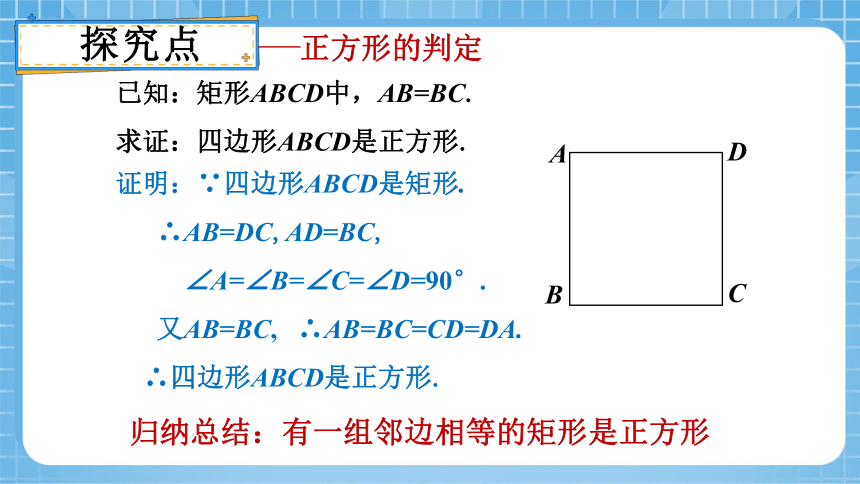
已知:矩形ABCD中,AB=BC.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形.
∴AB=DC,AD=BC,
∠A=∠B=∠C=∠D=90°.
又AB=BC, ∴AB=BC=CD=DA.
∴四边形ABCD是正方形.
归纳总结:有一组邻边相等的矩形是正方形
探究点
正方形的判定
我们再来看一个问题:
正方形的判定
探究点
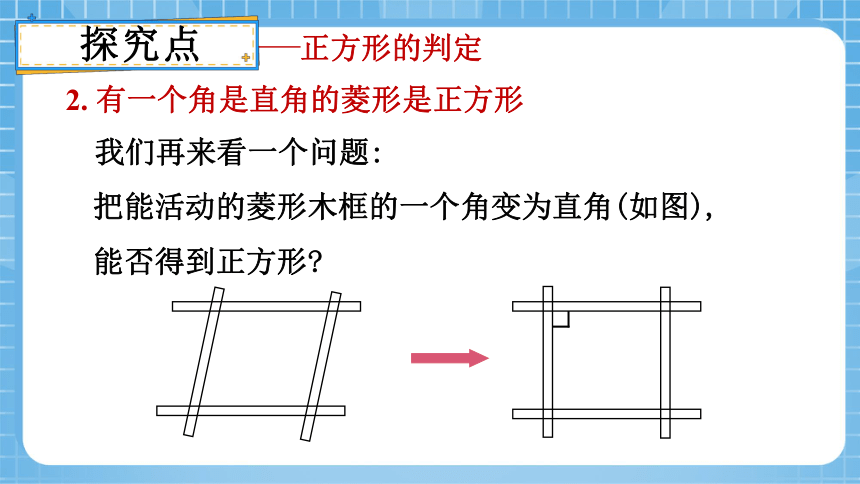
2. 有一个角是直角的菱形是正方形
把能活动的菱形木框的一个角变为直角(如图),能否得到正方形
正方形的判定
探究点
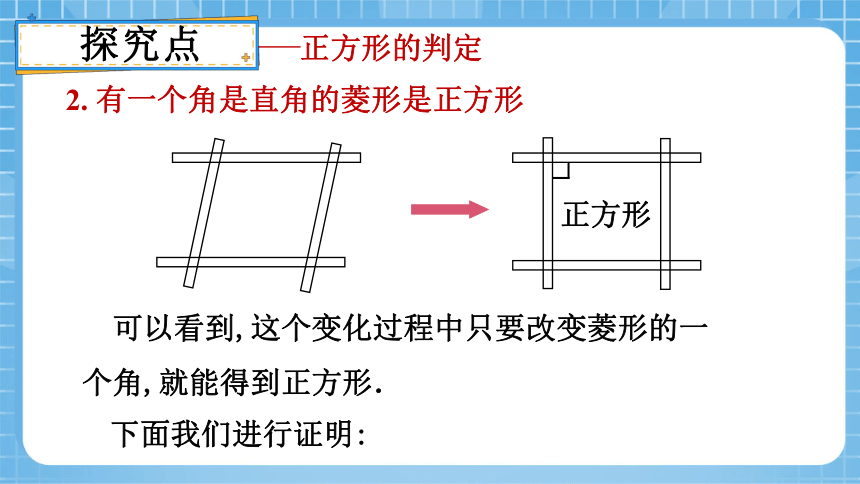
2. 有一个角是直角的菱形是正方形
可以看到,这个变化过程中只要改变菱形的一个角,就能得到正方形.
正方形
下面我们进行证明:
A
D
B
C
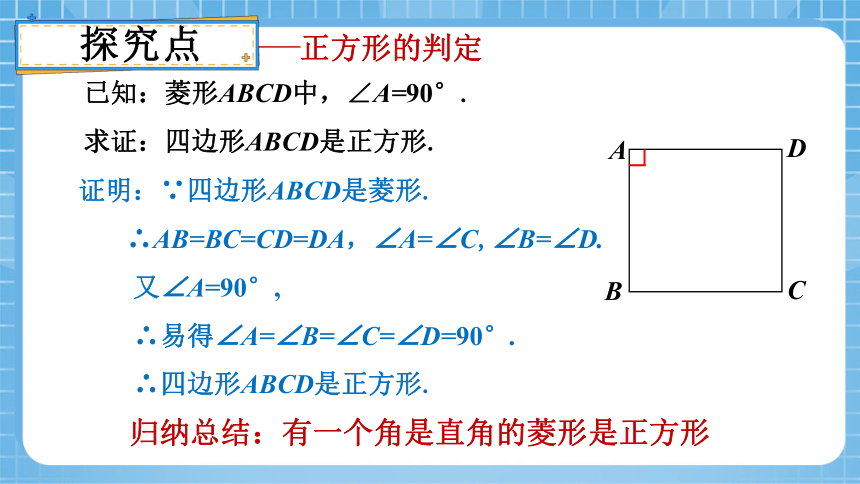
已知:菱形ABCD中,∠A=90°.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形.
∴AB=BC=CD=DA,∠A=∠C,∠B=∠D.
又∠A=90°,
∴易得∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是正方形.
归纳总结:有一个角是直角的菱形是正方形
探究点
正方形的判定
正方形的判定
探究点
在上面的证明过程中,是分别从矩形、菱形出发,添加边或角的条件后得到正方形,那么还有没有通过添加边、角、对角线的条件可以得到其他判定正方形的方法呢 大家想一想.
正方形的判定
探究点
从四边形出发 (1)四条边相等、四个角都是直角的四边形是正方形
(2)对角线互相垂直平分且相等的四边形是正方形
从平行四边形出发 (1)有一组邻边相等并且有一个角是直角的平行四边形是正方形
(2)对角线互相垂直且相等的平行四边形是正方形
从矩形出发 对角线互相垂直的矩形是正方形
从菱形出发 对角线相等的菱形是正方形
归纳总结:
正方形的判定
探究点
思考:上面给出了正方形的一些判定方法,这也蕴含了他们之间的转换关系,那么正方形、菱形、矩形、平行四边形之间有什么关系呢 与同学们讨论交流,并列表或用框图表示这些关系.
正方形的判定
整理归纳
正方形
平行四边形
矩形
菱形
进一步地,四边形、平行四边形、矩形、菱形、正方形有什么关系 有兴趣的同学可以整理下.
1. 如图,在△ABC中,点E,D,F分别在边AB,BC,
CA上,且DE∥CA, DF∥BA.
(1)四边形AEDF是 ;
(2)如果∠BAC=90°,那么四边形AEDF是 ;
(3)如果AD 平分∠BAC,那么四边形AEDF是 ;
(4)如果∠BAC=90°,AD平分∠BAC,那么四边形
AEDF是 .
对应训练
平行四边形
正方形
A
D
B
C
E
F
D
矩形
菱形
2. 满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.
对应训练
【选自教材P60,练习第3题】
是
是
是
是
例 如图,在矩形ABCD中,∠ABC的平分线交对角线AC于点E,EF⊥AB, EG⊥BC,垂足分别是F,G.判断四边形EFBG的形状,并证明你的结论.
例题精析
A
D
B
C
E
F
G
解:四边形EFBG是正方形.
证法1:∵四边形ABCD是矩形,∴∠ABC=90°.
又EF⊥AB,EG⊥BC,∴∠BFE=∠BGE=90°,
∴四边形EFBG是矩形.
∵BE为∠ABC的平分线,
∴EF=EG,
∴矩形EFBG是正方形.
例题精析
A
D
B
C
E
F
G
证法2:如图.∵四边形ABCD是矩形,∴∠ABC=90°.
∵BE为∠ABC的平分线,EF⊥AB,EG⊥BC,
∴∠1=∠2=45°,EF=EG.
∴∠3=∠4=45°,
∴∠1=∠3,∠2=∠4,∴BF=EF,BG=EG.
∴BF=EF=EG=BG,∴四边形EFBG是菱形.
又∠FBG=90°,∴菱形EFBG是正方形.
例题精析
A
D
B
C
E
F
G
1
2
3
4
如图,Rt△ABC的两条外角平分线相交于点D,∠B=90°,过点D分别作DE⊥BA于点E,DF⊥BC于点F.
(1)求证:四边形BFDE是正方形;
(2)若BF=6,C为BF的中点,求AE的长.
对应训练
A
B
C
F
D
E
(1)证明: 如图, 过点D作DH⊥AC于点H.
∵DE⊥BA , DF⊥BC, ∴∠E=∠F=∠B=90°,
∴四边形BFDE是矩形.
∵AD平分∠EAC, DE⊥BA , DH⊥AC,
∴DE=DH .
同理, DH=DF,
∴DE=DF, ∴矩形BFDE是正方形.
对应训练
C
A
B
F
D
E
H
(2)解:∵DH⊥AC,∴∠AHD=∠DHC=90°.
由(1)知∠E=∠F=90°,DE=DH, DH=DF.
∴∠AHD=∠DHC=∠E=∠F=90°.
在Rt△AED和Rt△AHD中,
∴Rt△AED≌Rt△AHD (HL),
∴AE=AH. 同理, CH=CF.
对应训练
A
B
C
F
D
E
H
DE=DH
DA=DA
∵BF=6, C为BF的中点, ∴BC=CF=CH=3.
∵四边形BFDE是正方形,∴BE=BF=6.
设AE=AH=x,则AB=BE-AE=6-x,
AC=AH+CH=x+3
在Rt△ABC中,由勾股定理,得AB2+BC2=AC2,
即(6-x)2+32=(x+3)2, 解得x=2,
∴AE的长为2.
对应训练
A
B
C
F
D
E
H
课堂总结
知识结构
正方形
平行四边形
矩形
菱形
四边形
课堂总结
知识结构
课堂总结
1. 教材P62习题18.2第13题.
1. 如图,E,F,M,N 分别是正方形ABCD四条边上的点,且AE=BF=CM=DN,试判断四边形EFMN是什么图形,并证明你的结论.
A
D
B
C
E
F
M
N
1
2
3
正方形的性质
三角形全等
正方形
点击查看解题过程
课后作业
【选自教材P62,习题18.2第13题】
解:四边形EFMN是正方形.
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA.
又AE=BF=CM=DN,
∴BE=CF=DM=AN.
又∠A=∠B=∠C=∠D=90°,
∴△AEN≌△BFE≌△CMF≌△DNM,
∠1+∠3=90°.
∴∠1=∠2,EN=FE=MF=NM.
∴∠2+∠3=90°. ∴∠NEF=90°.
同理可得:∠EFM=∠FMN=∠MNE=90°.
∴四边形EFMN是正方形.
A
D
B
C
E
F
M
N
1
2
3
课后作业
2. 如图,已知在□ ABCD中,对角线AC,BD相交于点O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
课后作业
1
证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC.
又EA=EC,
∴EO⊥AC.
即BD⊥AC.
∴四边形ABCD是菱形.
(2)∵∠DAC=∠EAD+∠AED,
而∠1=∠EAD+∠AED,
∴∠DAC=∠1.
∴OA=OD.
又四边形ABCD是菱形,
∴AC=2OA=2OD=BD.
∴四边形ABCD是正方形.
课后作业
3. 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD ,PN⊥CD,垂足分别为M ,N.
(1)求证:∠ADB=∠CDB.
(2)若∠ADC=90 ,求证:四边形PMDN是正方形.
C
A
B
D
M
N
P
课后作业
证明:(1)∵BD平分∠ABC,
∴∠1=∠2.
又AB=CB, BD=BD,
∴△ABD≌△CBD(SAS).
∴∠ADB=∠CDB.
C
A
B
D
M
N
P
1
2
课后作业
(2)∵∠ADC=90°,PM⊥AD , PN⊥CD,
∴∠ADC=∠PMD=∠PND=90°.
∴四边形PMDN是矩形.
又 由(1)可知 :BD是∠ADC 的角平分线,
∴PM=PN.
∴四边形OMDN是正方形.
正方形的判定
第十八章 平行四边形
正方形的自我介绍:在四边形的大家庭中,我有四个兄弟.
老大是平行四边形,它性格温和;老二是矩形,它稳重大方,江湖上人称长方形;老三是菱形,它活泼可爱.我就是正方形老四,我集三位大哥的优点于一身,人见人爱.
回顾导入
到目前为止,我们已经认识了四边形大家庭的成员,前一课时,我们大致介绍了矩形、菱形、平行四边形与正方形的关系,并给出了下面的结构图.
回顾导入
平行四边形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
正方形
可以看到矩形、菱形各添加一个条件都能得到正方形,那么这个是否可以证明呢 我们这节课来看下.
回顾导入
平行四边形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
正方形
我们来看下面这个问题:
正方形的判定
探究点
1. 有一组邻边相等的矩形是正方形
把一张矩形的纸片按图中那样折一下,是否可以截出正方形纸片
正方形的判定
探究点
1. 有一组邻边相等的矩形是正方形
答案是肯定的,它的依据就是有一组邻边相等的矩形是正方形.
下面我们进行证明:
A
D
B
C
已知:矩形ABCD中,AB=BC.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形.
∴AB=DC,AD=BC,
∠A=∠B=∠C=∠D=90°.
又AB=BC, ∴AB=BC=CD=DA.
∴四边形ABCD是正方形.
归纳总结:有一组邻边相等的矩形是正方形
探究点
正方形的判定
我们再来看一个问题:
正方形的判定
探究点
2. 有一个角是直角的菱形是正方形
把能活动的菱形木框的一个角变为直角(如图),能否得到正方形
正方形的判定
探究点
2. 有一个角是直角的菱形是正方形
可以看到,这个变化过程中只要改变菱形的一个角,就能得到正方形.
正方形
下面我们进行证明:
A
D
B
C
已知:菱形ABCD中,∠A=90°.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形.
∴AB=BC=CD=DA,∠A=∠C,∠B=∠D.
又∠A=90°,
∴易得∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是正方形.
归纳总结:有一个角是直角的菱形是正方形
探究点
正方形的判定
正方形的判定
探究点
在上面的证明过程中,是分别从矩形、菱形出发,添加边或角的条件后得到正方形,那么还有没有通过添加边、角、对角线的条件可以得到其他判定正方形的方法呢 大家想一想.
正方形的判定
探究点
从四边形出发 (1)四条边相等、四个角都是直角的四边形是正方形
(2)对角线互相垂直平分且相等的四边形是正方形
从平行四边形出发 (1)有一组邻边相等并且有一个角是直角的平行四边形是正方形
(2)对角线互相垂直且相等的平行四边形是正方形
从矩形出发 对角线互相垂直的矩形是正方形
从菱形出发 对角线相等的菱形是正方形
归纳总结:
正方形的判定
探究点
思考:上面给出了正方形的一些判定方法,这也蕴含了他们之间的转换关系,那么正方形、菱形、矩形、平行四边形之间有什么关系呢 与同学们讨论交流,并列表或用框图表示这些关系.
正方形的判定
整理归纳
正方形
平行四边形
矩形
菱形
进一步地,四边形、平行四边形、矩形、菱形、正方形有什么关系 有兴趣的同学可以整理下.
1. 如图,在△ABC中,点E,D,F分别在边AB,BC,
CA上,且DE∥CA, DF∥BA.
(1)四边形AEDF是 ;
(2)如果∠BAC=90°,那么四边形AEDF是 ;
(3)如果AD 平分∠BAC,那么四边形AEDF是 ;
(4)如果∠BAC=90°,AD平分∠BAC,那么四边形
AEDF是 .
对应训练
平行四边形
正方形
A
D
B
C
E
F
D
矩形
菱形
2. 满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.
对应训练
【选自教材P60,练习第3题】
是
是
是
是
例 如图,在矩形ABCD中,∠ABC的平分线交对角线AC于点E,EF⊥AB, EG⊥BC,垂足分别是F,G.判断四边形EFBG的形状,并证明你的结论.
例题精析
A
D
B
C
E
F
G
解:四边形EFBG是正方形.
证法1:∵四边形ABCD是矩形,∴∠ABC=90°.
又EF⊥AB,EG⊥BC,∴∠BFE=∠BGE=90°,
∴四边形EFBG是矩形.
∵BE为∠ABC的平分线,
∴EF=EG,
∴矩形EFBG是正方形.
例题精析
A
D
B
C
E
F
G
证法2:如图.∵四边形ABCD是矩形,∴∠ABC=90°.
∵BE为∠ABC的平分线,EF⊥AB,EG⊥BC,
∴∠1=∠2=45°,EF=EG.
∴∠3=∠4=45°,
∴∠1=∠3,∠2=∠4,∴BF=EF,BG=EG.
∴BF=EF=EG=BG,∴四边形EFBG是菱形.
又∠FBG=90°,∴菱形EFBG是正方形.
例题精析
A
D
B
C
E
F
G
1
2
3
4
如图,Rt△ABC的两条外角平分线相交于点D,∠B=90°,过点D分别作DE⊥BA于点E,DF⊥BC于点F.
(1)求证:四边形BFDE是正方形;
(2)若BF=6,C为BF的中点,求AE的长.
对应训练
A
B
C
F
D
E
(1)证明: 如图, 过点D作DH⊥AC于点H.
∵DE⊥BA , DF⊥BC, ∴∠E=∠F=∠B=90°,
∴四边形BFDE是矩形.
∵AD平分∠EAC, DE⊥BA , DH⊥AC,
∴DE=DH .
同理, DH=DF,
∴DE=DF, ∴矩形BFDE是正方形.
对应训练
C
A
B
F
D
E
H
(2)解:∵DH⊥AC,∴∠AHD=∠DHC=90°.
由(1)知∠E=∠F=90°,DE=DH, DH=DF.
∴∠AHD=∠DHC=∠E=∠F=90°.
在Rt△AED和Rt△AHD中,
∴Rt△AED≌Rt△AHD (HL),
∴AE=AH. 同理, CH=CF.
对应训练
A
B
C
F
D
E
H
DE=DH
DA=DA
∵BF=6, C为BF的中点, ∴BC=CF=CH=3.
∵四边形BFDE是正方形,∴BE=BF=6.
设AE=AH=x,则AB=BE-AE=6-x,
AC=AH+CH=x+3
在Rt△ABC中,由勾股定理,得AB2+BC2=AC2,
即(6-x)2+32=(x+3)2, 解得x=2,
∴AE的长为2.
对应训练
A
B
C
F
D
E
H
课堂总结
知识结构
正方形
平行四边形
矩形
菱形
四边形
课堂总结
知识结构
课堂总结
1. 教材P62习题18.2第13题.
1. 如图,E,F,M,N 分别是正方形ABCD四条边上的点,且AE=BF=CM=DN,试判断四边形EFMN是什么图形,并证明你的结论.
A
D
B
C
E
F
M
N
1
2
3
正方形的性质
三角形全等
正方形
点击查看解题过程
课后作业
【选自教材P62,习题18.2第13题】
解:四边形EFMN是正方形.
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA.
又AE=BF=CM=DN,
∴BE=CF=DM=AN.
又∠A=∠B=∠C=∠D=90°,
∴△AEN≌△BFE≌△CMF≌△DNM,
∠1+∠3=90°.
∴∠1=∠2,EN=FE=MF=NM.
∴∠2+∠3=90°. ∴∠NEF=90°.
同理可得:∠EFM=∠FMN=∠MNE=90°.
∴四边形EFMN是正方形.
A
D
B
C
E
F
M
N
1
2
3
课后作业
2. 如图,已知在□ ABCD中,对角线AC,BD相交于点O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
课后作业
1
证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC.
又EA=EC,
∴EO⊥AC.
即BD⊥AC.
∴四边形ABCD是菱形.
(2)∵∠DAC=∠EAD+∠AED,
而∠1=∠EAD+∠AED,
∴∠DAC=∠1.
∴OA=OD.
又四边形ABCD是菱形,
∴AC=2OA=2OD=BD.
∴四边形ABCD是正方形.
课后作业
3. 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD ,PN⊥CD,垂足分别为M ,N.
(1)求证:∠ADB=∠CDB.
(2)若∠ADC=90 ,求证:四边形PMDN是正方形.
C
A
B
D
M
N
P
课后作业
证明:(1)∵BD平分∠ABC,
∴∠1=∠2.
又AB=CB, BD=BD,
∴△ABD≌△CBD(SAS).
∴∠ADB=∠CDB.
C
A
B
D
M
N
P
1
2
课后作业
(2)∵∠ADC=90°,PM⊥AD , PN⊥CD,
∴∠ADC=∠PMD=∠PND=90°.
∴四边形PMDN是矩形.
又 由(1)可知 :BD是∠ADC 的角平分线,
∴PM=PN.
∴四边形OMDN是正方形.
