18.2.2菱形 菱形的性质 课件(共31张PPT) 人教版数学八年级下册
文档属性
| 名称 | 18.2.2菱形 菱形的性质 课件(共31张PPT) 人教版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 19:53:45 | ||
图片预览




文档简介
(共31张PPT)
第十八章 平行四边形
菱形的性质
情境导入
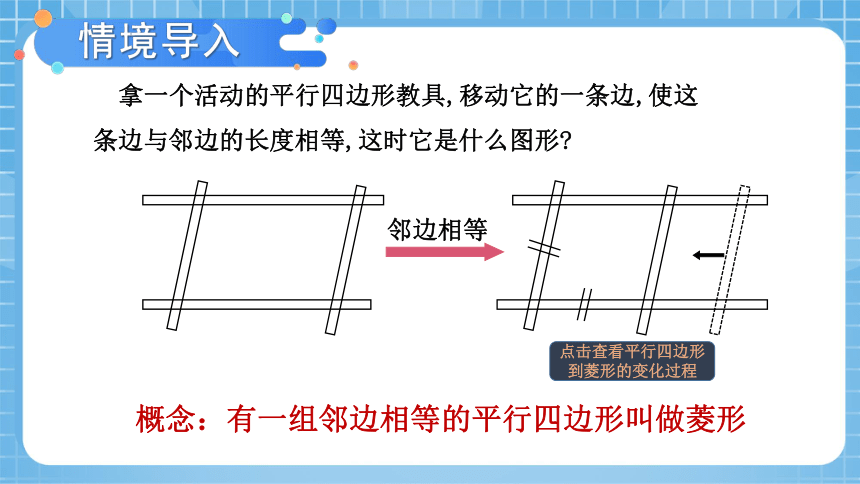
拿一个活动的平行四边形教具,移动它的一条边,使这条边与邻边的长度相等,这时它是什么图形
点击查看平行四边形到菱形的变化过程
概念:有一组邻边相等的平行四边形叫做菱形
邻边相等
情境导入
仔细观察下列实际生活中的图片,你觉得哪些是菱形的形象
菱形是生活中很常见的图形,你还能列举出菱形在生活中应用的其他例子吗 我们一起来探讨一下菱形的性质吧!
探究点1
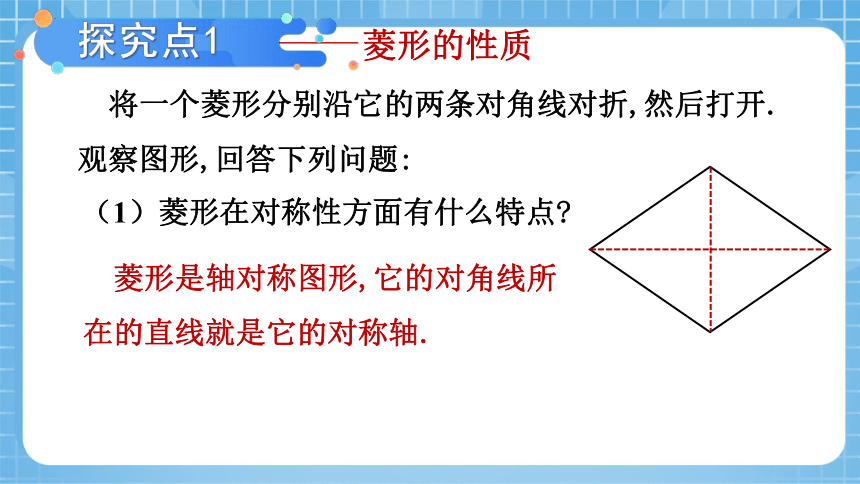
将一个菱形分别沿它的两条对角线对折,然后打开.
观察图形,回答下列问题:
(1)菱形在对称性方面有什么特点
菱形的性质
菱形是轴对称图形,它的对角线所在的直线就是它的对称轴.
菱形在平行四边形的基础上多了邻边相等的条件.
探究点1
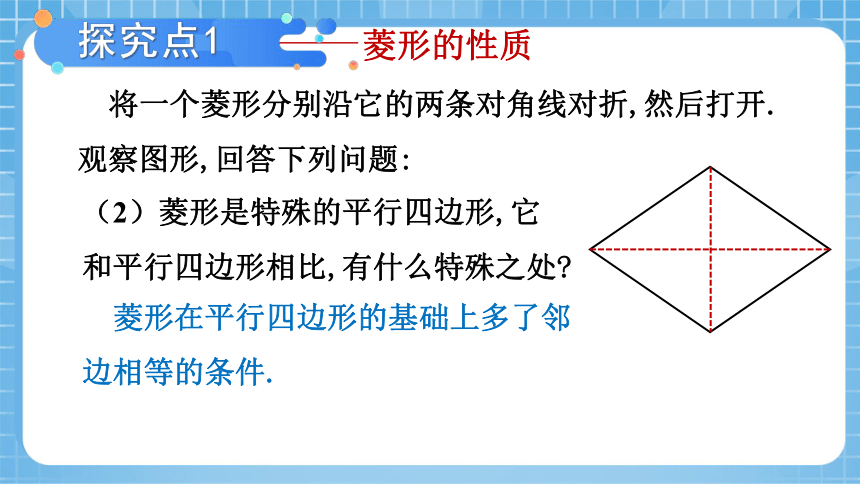
将一个菱形分别沿它的两条对角线对折,然后打开.
观察图形,回答下列问题:
(2)菱形是特殊的平行四边形,它和平行四边形相比,有什么特殊之处
菱形的性质
由于菱形是有一组邻边相等的平行四边形,由平行四边形对边相等的性质容易发现菱形的四条边都相等.
探究点1
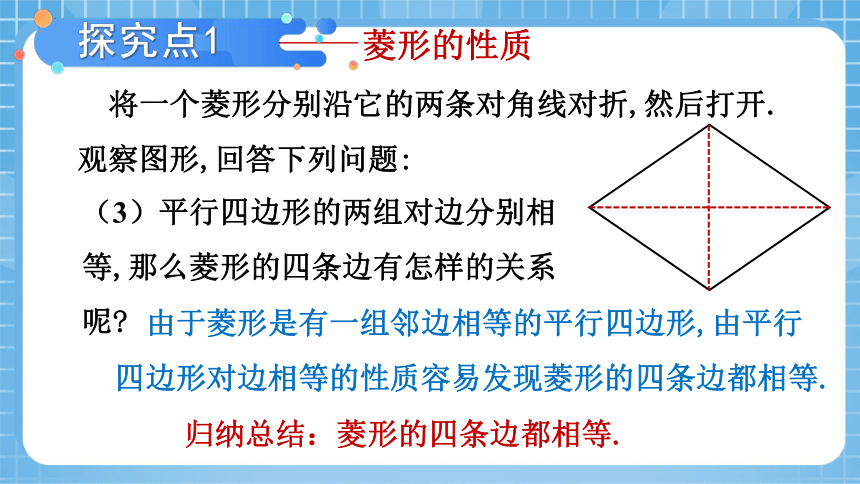
将一个菱形分别沿它的两条对角线对折,然后打开.
观察图形,回答下列问题:
(3)平行四边形的两组对边分别相等,那么菱形的四条边有怎样的关系呢
菱形的性质
归纳总结:菱形的四条边都相等.
探究点1
将一个菱形分别沿它的两条对角线对折,然后打开.
观察图形,回答下列问题:
(4)我们通过刚刚的折纸,可以发现菱形的两条对角线有什么位置关系
菱形的性质
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
下面我们来试着证明这条性质:
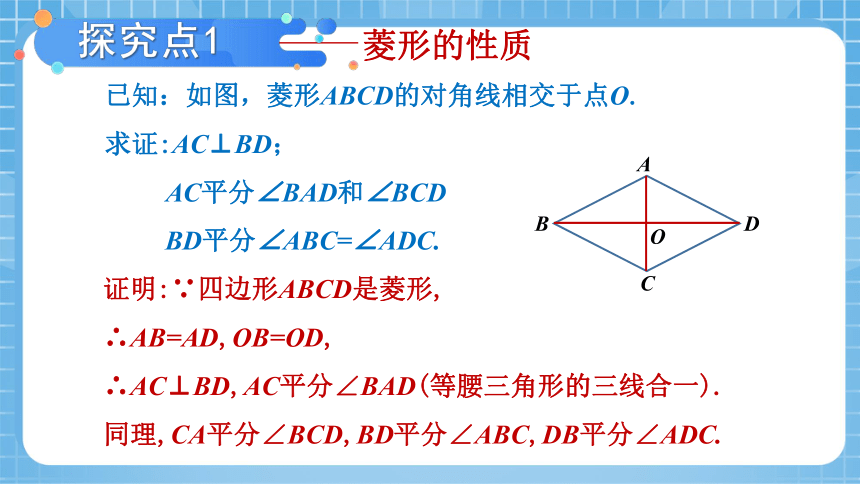
已知:如图,菱形ABCD的对角线相交于点O.
求证:AC⊥BD;
AC平分∠BAD和∠BCD
BD平分∠ABC=∠ADC.
B
C
D
A
O
探究点1
菱形的性质
证明:∵四边形ABCD是菱形,
∴AB=AD,OB=OD,
∴AC⊥BD,AC平分∠BAD(等腰三角形的三线合一).
同理,CA平分∠BCD,BD平分∠ABC,DB平分∠ADC.
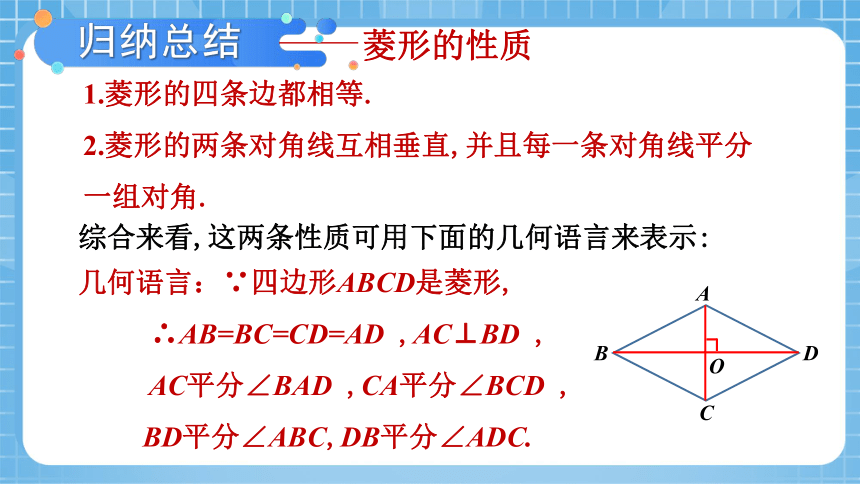
1.菱形的四条边都相等.
2.菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
几何语言:∵四边形ABCD是菱形,
∴AB=BC=CD=AD ,AC⊥BD ,
AC平分∠BAD ,CA平分∠BCD ,
BD平分∠ABC,DB平分∠ADC.
归纳总结
综合来看,这两条性质可用下面的几何语言来表示:
B
C
D
A
O
菱形的性质
1. 菱形不具有的性质是( )
对应训练
A. 四条边都相等 B. 对角线相等
C. 是轴对称图形 D. 是中心对称图形
B
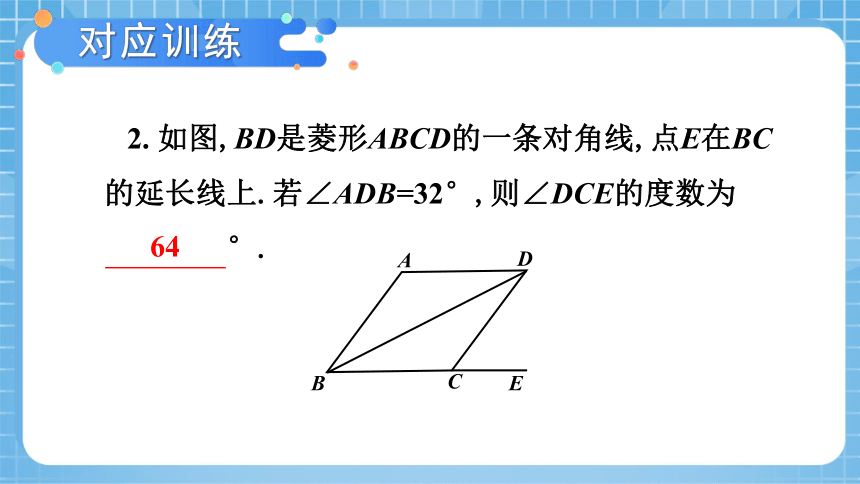
对应训练
2. 如图,BD是菱形ABCD的一条对角线,点E在BC 的延长线上.若∠ADB=32°,则∠DCE的度数为
°.
64
A
B
C
D
E
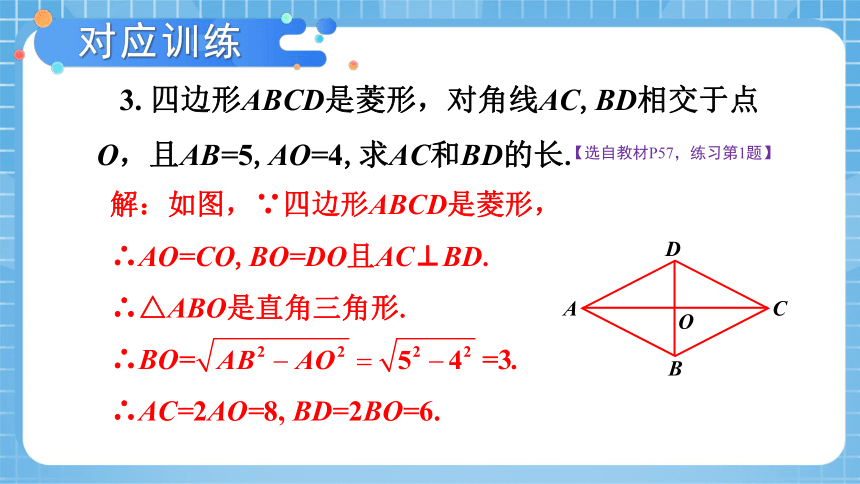
3. 四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4,求AC和BD的长.
对应训练
【选自教材P57,练习第1题】
解:如图,∵四边形ABCD是菱形,
∴AO=CO,BO=DO且AC⊥BD.
∴△ABO是直角三角形.
∴BO= =3.
∴AC=2AO=8, BD=2BO=6.
A
B
C
D
O
探究点2
将由于菱形的对角线互相垂直,我们发现,菱形的对角线可以把菱形分成四个全等的直角三角形.
那么菱形的面积计算除了像平行四边形那样利用底×高,是否可以转化成三角形来求得
菱形的面积
菱形的面积还可以利用4个全等的三角形面积的和来计算.
B
C
D
A
O
归纳总结:菱形被它的两条对角线分成四个全等的直角三角形,它们的底和高分别是两条对角线的一半.所以利用三角形的面积公式可以得到,菱形的面积等于它的两条对角线长的积的一半.
菱形面积推导
B
C
D
A
O
菱形的面积=对角线长的积的一半
例1 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
A
B
C
D
O
例题精析
解:∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO= ∠ABC= 60°=30°.
在Rt△OAB中,
AO= AB= 20=10
∴花坛的两条小路长
AC=2AO=20(m),BD=2BO=20 ≈34.64(m)
花坛的面积
A
B
C
D
O
20m
60°
例题精析
1. 已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积.
对应训练
【选自教材P57,练习第2题】
A
C
B
D
O
解:如图,∵四边形ABCD是菱形,
∴AO=CO,BO=DO且AC⊥BD.
∵AC=8,BD=6,∴AO=4,BO=3.
在Rt△AOB中,由勾股定理得
AB= =5,
∴菱形的周长为20,菱形的面积为24.
2. 小雨在参观故宫博物院时,被太和殿窗棂的三交六椀菱花图案所吸引,他从中提取出一个含60°角的菱形ABCD(如图).若AB的长度为2,求菱形ABCD的面积.
对应训练
B
D
A
C
60°
对应训练
解:如图,过点A作AH⊥BC于点H.
∵四边形ABCD是菱形,∴BC=AB=2.
∵∠B=60°,∴∠BAH=90°-∠B=30°,
△ABC 是等边三角形.
∴BH= AB=1.
由勾股定理易得AH= ,
∴菱形ABCD的面积为BC·AH=2× = .
B
D
A
C
H
60°
例2 如图,在菱形ABCD中, 过点B分别作BM⊥
AD 于点M, BN⊥CD于点N , BM , BN分别交AC于点
E, F. 求证: AE=CF.
例题精析
A
C
B
D
E
F
M
N
例题精析
解:∵四边形ABCD 为菱形,
∴AB=CB,∠BAM=∠BCN ,∠BAE=∠DAE=∠DCF=∠BCF.
∵BM⊥AD ,BN⊥CD ,∴∠AMB=∠CNB=90°.
∴∠BAM+∠ABE=90°,∠BCN+∠CBF=90°,
∴∠ABE=∠CBF.
在△ABE和△CBF中,
∴△ABE≌△CBF(ASA),∴AE=CF.
∠BAE=∠BCF
AB=CB
∠ABE=∠CBF
A
C
B
D
E
F
M
N
1. 已知:如图,在菱形ABCD中,对角线AC与BD 交于点O,∠BAD=120°,AC=4,则该菱形的面积是 .
对应训练
A
B
C
D
O
2. 如图,四边形ABCD是菱形,F是AB上一点,DF交AC于点E,连接BE. 求证:∠AFD=∠CBE.
对应训练
解:∵四边形ABCD是菱形,
∴AB∥CD,CB=CD,CA平分∠BCD.
∴∠BCE=∠DCE.
又CE=CE, ∴△BCE≌△DCE(SAS).
∴∠CBE=∠CDE.∵AB∥CD ,
∴∠AFD=∠CDE.∴∠AFD=∠CBE.
A
B
C
D
F
E
知识结构:
课堂总结
平行四边形
菱形
四条边都相等
两条对角线互相垂直,并且每一条对角线平分一组对角
课后作业
1. 教材P60习题18.2第5, 11题.
1. 如图,四边形ABCD是菱形,∠ACD=30°,BD=6,
求:(1)∠BAD,∠ABC的度数;
(2)AB,AC的长.
A
C
D
B
课后作业
【选自教材P60,习题18.2第5题】
解:(1)∵四边形ABCD是菱形
∴AC平分∠BCD.
∴∠BCD=2∠ACD=2×30°=60°.
∴∠BAD=∠BCD=60°.
又∠ABC+∠BAD=180°,
∴∠ABC=180°-∠BAD=180°-60°=120°
课后作业
A
C
D
B
课后作业
A
C
D
B
O
(2)设AC与BD交于点O,
由(1)知∠BAD=60°,AB=AD,
∴△ABD是等边三角形.
∴AB=BD=6.
在Rt△ABO中,AB=6,BO= BD=3,
∴AO= ,
∴AC=2AO= .
2. 如图,四边形ABCD是菱形,AC=8,BD=6,
DH⊥AB于点H,求DH的长.
∴AB=
解:∵四边形ABCD是菱形
∴OA= AC=4,OB= BD=3
∴AB=
又 =24
A
C
D
O
H
B
课后作业
【选自教材P61,习题18.2第11题】
3. 已知:菱形ABCD中,E是BC的中点,且AE⊥BC, BC=a,
则(1)∠BCD的度数 ;
(2)对角线BD的长 ;
(3)菱形ABCD的面积 .
A
B
C
D
a
E
O
120°
课后作业
4. 如图,在菱形ABCD中,AB=4a,E在BC上,EC=2a, ∠BAD=120°,点P在BD上,则PE+PC的最小值是 .
A
B
C
D
P
E
4a
120°
2a
课后作业
第十八章 平行四边形
菱形的性质
情境导入
拿一个活动的平行四边形教具,移动它的一条边,使这条边与邻边的长度相等,这时它是什么图形
点击查看平行四边形到菱形的变化过程
概念:有一组邻边相等的平行四边形叫做菱形
邻边相等
情境导入
仔细观察下列实际生活中的图片,你觉得哪些是菱形的形象
菱形是生活中很常见的图形,你还能列举出菱形在生活中应用的其他例子吗 我们一起来探讨一下菱形的性质吧!
探究点1
将一个菱形分别沿它的两条对角线对折,然后打开.
观察图形,回答下列问题:
(1)菱形在对称性方面有什么特点
菱形的性质
菱形是轴对称图形,它的对角线所在的直线就是它的对称轴.
菱形在平行四边形的基础上多了邻边相等的条件.
探究点1
将一个菱形分别沿它的两条对角线对折,然后打开.
观察图形,回答下列问题:
(2)菱形是特殊的平行四边形,它和平行四边形相比,有什么特殊之处
菱形的性质
由于菱形是有一组邻边相等的平行四边形,由平行四边形对边相等的性质容易发现菱形的四条边都相等.
探究点1
将一个菱形分别沿它的两条对角线对折,然后打开.
观察图形,回答下列问题:
(3)平行四边形的两组对边分别相等,那么菱形的四条边有怎样的关系呢
菱形的性质
归纳总结:菱形的四条边都相等.
探究点1
将一个菱形分别沿它的两条对角线对折,然后打开.
观察图形,回答下列问题:
(4)我们通过刚刚的折纸,可以发现菱形的两条对角线有什么位置关系
菱形的性质
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
下面我们来试着证明这条性质:
已知:如图,菱形ABCD的对角线相交于点O.
求证:AC⊥BD;
AC平分∠BAD和∠BCD
BD平分∠ABC=∠ADC.
B
C
D
A
O
探究点1
菱形的性质
证明:∵四边形ABCD是菱形,
∴AB=AD,OB=OD,
∴AC⊥BD,AC平分∠BAD(等腰三角形的三线合一).
同理,CA平分∠BCD,BD平分∠ABC,DB平分∠ADC.
1.菱形的四条边都相等.
2.菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
几何语言:∵四边形ABCD是菱形,
∴AB=BC=CD=AD ,AC⊥BD ,
AC平分∠BAD ,CA平分∠BCD ,
BD平分∠ABC,DB平分∠ADC.
归纳总结
综合来看,这两条性质可用下面的几何语言来表示:
B
C
D
A
O
菱形的性质
1. 菱形不具有的性质是( )
对应训练
A. 四条边都相等 B. 对角线相等
C. 是轴对称图形 D. 是中心对称图形
B
对应训练
2. 如图,BD是菱形ABCD的一条对角线,点E在BC 的延长线上.若∠ADB=32°,则∠DCE的度数为
°.
64
A
B
C
D
E
3. 四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4,求AC和BD的长.
对应训练
【选自教材P57,练习第1题】
解:如图,∵四边形ABCD是菱形,
∴AO=CO,BO=DO且AC⊥BD.
∴△ABO是直角三角形.
∴BO= =3.
∴AC=2AO=8, BD=2BO=6.
A
B
C
D
O
探究点2
将由于菱形的对角线互相垂直,我们发现,菱形的对角线可以把菱形分成四个全等的直角三角形.
那么菱形的面积计算除了像平行四边形那样利用底×高,是否可以转化成三角形来求得
菱形的面积
菱形的面积还可以利用4个全等的三角形面积的和来计算.
B
C
D
A
O
归纳总结:菱形被它的两条对角线分成四个全等的直角三角形,它们的底和高分别是两条对角线的一半.所以利用三角形的面积公式可以得到,菱形的面积等于它的两条对角线长的积的一半.
菱形面积推导
B
C
D
A
O
菱形的面积=对角线长的积的一半
例1 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
A
B
C
D
O
例题精析
解:∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO= ∠ABC= 60°=30°.
在Rt△OAB中,
AO= AB= 20=10
∴花坛的两条小路长
AC=2AO=20(m),BD=2BO=20 ≈34.64(m)
花坛的面积
A
B
C
D
O
20m
60°
例题精析
1. 已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积.
对应训练
【选自教材P57,练习第2题】
A
C
B
D
O
解:如图,∵四边形ABCD是菱形,
∴AO=CO,BO=DO且AC⊥BD.
∵AC=8,BD=6,∴AO=4,BO=3.
在Rt△AOB中,由勾股定理得
AB= =5,
∴菱形的周长为20,菱形的面积为24.
2. 小雨在参观故宫博物院时,被太和殿窗棂的三交六椀菱花图案所吸引,他从中提取出一个含60°角的菱形ABCD(如图).若AB的长度为2,求菱形ABCD的面积.
对应训练
B
D
A
C
60°
对应训练
解:如图,过点A作AH⊥BC于点H.
∵四边形ABCD是菱形,∴BC=AB=2.
∵∠B=60°,∴∠BAH=90°-∠B=30°,
△ABC 是等边三角形.
∴BH= AB=1.
由勾股定理易得AH= ,
∴菱形ABCD的面积为BC·AH=2× = .
B
D
A
C
H
60°
例2 如图,在菱形ABCD中, 过点B分别作BM⊥
AD 于点M, BN⊥CD于点N , BM , BN分别交AC于点
E, F. 求证: AE=CF.
例题精析
A
C
B
D
E
F
M
N
例题精析
解:∵四边形ABCD 为菱形,
∴AB=CB,∠BAM=∠BCN ,∠BAE=∠DAE=∠DCF=∠BCF.
∵BM⊥AD ,BN⊥CD ,∴∠AMB=∠CNB=90°.
∴∠BAM+∠ABE=90°,∠BCN+∠CBF=90°,
∴∠ABE=∠CBF.
在△ABE和△CBF中,
∴△ABE≌△CBF(ASA),∴AE=CF.
∠BAE=∠BCF
AB=CB
∠ABE=∠CBF
A
C
B
D
E
F
M
N
1. 已知:如图,在菱形ABCD中,对角线AC与BD 交于点O,∠BAD=120°,AC=4,则该菱形的面积是 .
对应训练
A
B
C
D
O
2. 如图,四边形ABCD是菱形,F是AB上一点,DF交AC于点E,连接BE. 求证:∠AFD=∠CBE.
对应训练
解:∵四边形ABCD是菱形,
∴AB∥CD,CB=CD,CA平分∠BCD.
∴∠BCE=∠DCE.
又CE=CE, ∴△BCE≌△DCE(SAS).
∴∠CBE=∠CDE.∵AB∥CD ,
∴∠AFD=∠CDE.∴∠AFD=∠CBE.
A
B
C
D
F
E
知识结构:
课堂总结
平行四边形
菱形
四条边都相等
两条对角线互相垂直,并且每一条对角线平分一组对角
课后作业
1. 教材P60习题18.2第5, 11题.
1. 如图,四边形ABCD是菱形,∠ACD=30°,BD=6,
求:(1)∠BAD,∠ABC的度数;
(2)AB,AC的长.
A
C
D
B
课后作业
【选自教材P60,习题18.2第5题】
解:(1)∵四边形ABCD是菱形
∴AC平分∠BCD.
∴∠BCD=2∠ACD=2×30°=60°.
∴∠BAD=∠BCD=60°.
又∠ABC+∠BAD=180°,
∴∠ABC=180°-∠BAD=180°-60°=120°
课后作业
A
C
D
B
课后作业
A
C
D
B
O
(2)设AC与BD交于点O,
由(1)知∠BAD=60°,AB=AD,
∴△ABD是等边三角形.
∴AB=BD=6.
在Rt△ABO中,AB=6,BO= BD=3,
∴AO= ,
∴AC=2AO= .
2. 如图,四边形ABCD是菱形,AC=8,BD=6,
DH⊥AB于点H,求DH的长.
∴AB=
解:∵四边形ABCD是菱形
∴OA= AC=4,OB= BD=3
∴AB=
又 =24
A
C
D
O
H
B
课后作业
【选自教材P61,习题18.2第11题】
3. 已知:菱形ABCD中,E是BC的中点,且AE⊥BC, BC=a,
则(1)∠BCD的度数 ;
(2)对角线BD的长 ;
(3)菱形ABCD的面积 .
A
B
C
D
a
E
O
120°
课后作业
4. 如图,在菱形ABCD中,AB=4a,E在BC上,EC=2a, ∠BAD=120°,点P在BD上,则PE+PC的最小值是 .
A
B
C
D
P
E
4a
120°
2a
课后作业
