2023—2024学年浙教版数学九年级上册 期末拔高试题(无答案)
文档属性
| 名称 | 2023—2024学年浙教版数学九年级上册 期末拔高试题(无答案) | 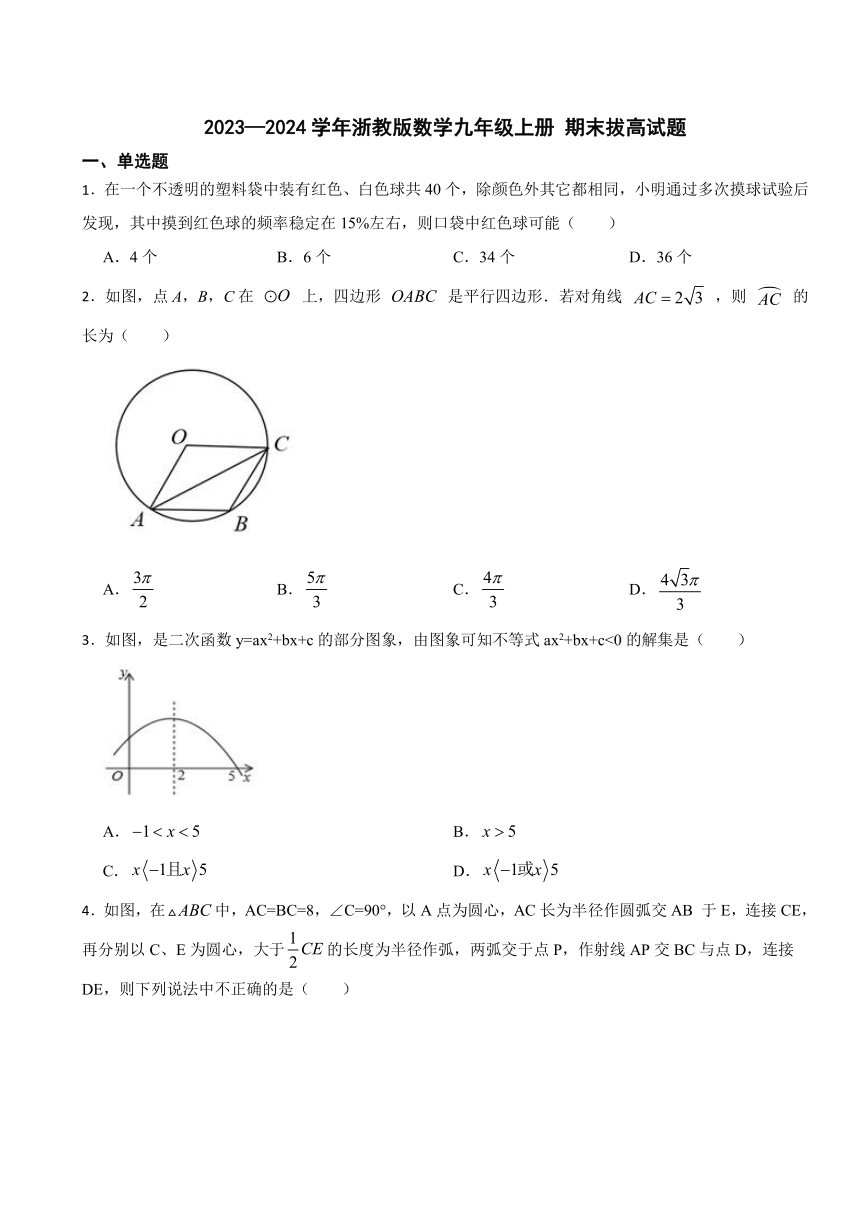 | |
| 格式 | docx | ||
| 文件大小 | 192.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-31 19:45:17 | ||
图片预览


文档简介
2023—2024学年浙教版数学九年级上册 期末拔高试题
一、单选题
1.在一个不透明的塑料袋中装有红色、白色球共40个,除颜色外其它都相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能( )
A.4个 B.6个 C.34个 D.36个
2.如图,点A,B,C在 上,四边形 是平行四边形.若对角线 ,则 的长为( )
A. B. C. D.
3.如图,是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
A. B.
C. D.
4.如图,在中,AC=BC=8,∠C=90°,以A点为圆心,AC长为半径作圆弧交AB 于E,连接CE,再分别以C、E为圆心,大于的长度为半径作弧,两弧交于点P,作射线AP交BC与点D,连接DE,则下列说法中不正确的是( )
A. B.
C. D.
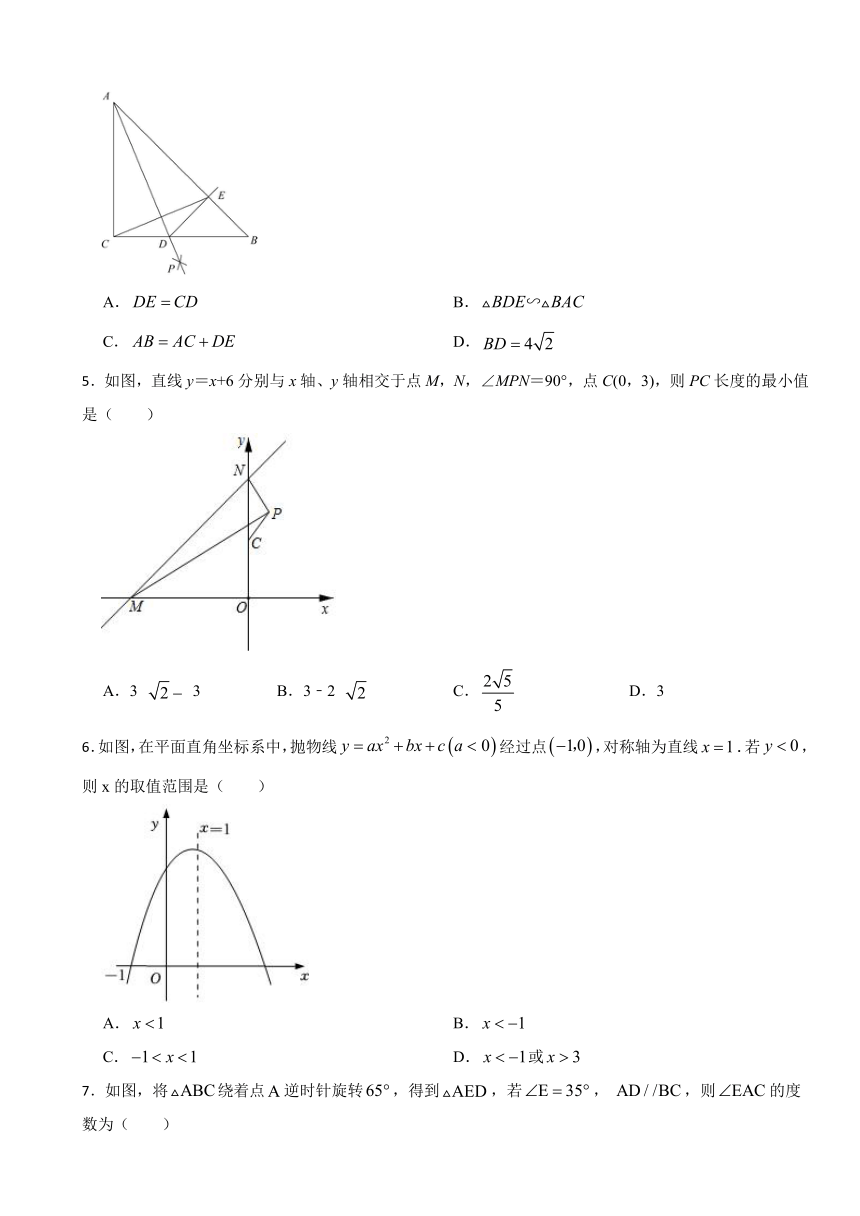
5.如图,直线y=x+6分别与x轴、y轴相交于点M,N,∠MPN=90°,点C(0,3),则PC长度的最小值是( )
A.3 3 B.3﹣2 C. D.3
6.如图,在平面直角坐标系中,抛物线经过点,对称轴为直线.若,则x的取值范围是( )
A. B.
C. D.或
7.如图,将绕着点逆时针旋转,得到,若,,则的度数为( )
A. B. C. D.
8.若关于x的不等式组有解,则函数y=(a 3)x2 x 图象与x轴的交点个数为( )
A.0 B.1 C.2 D.1或2
9.如图,在国旗台DF上有一根旗杆AF,国庆节当天小明参加升旗仪式,在B处测得旗杆顶端的仰角为37°,小明向前走4米到达点E,经过坡度为1的坡面DE,坡面的水平距离是1米,到达点D,测得此时旗杆顶端的仰角为53°,则旗杆的高度约为( )米.(参考数据: , , )
A.6.29 B.4.71 C.4 D.5.33
10.已知二次函数的图象经过与两点,关于的一元二次方程有两个不同的实数根,其中一个根是如果关于的方程有两个不同的整数,则这两个整数根可能是( )
A., B.,
C., D.,
二、填空题
11.在2,-2,0三个整数中,任取一个,恰好使分式 有意义的概率是 。
12.如图,矩形ABCD是由两个边长为1的小正方形拼成,图中阴影部分是以B、D为圆心半径为1的两个小扇形,则这两个阴影部分面积之和为 .
13.甲、乙两个袋子中各装有2个相同的小球,分别写有数字1和2.从两个袋子中各随机取出1个小球,球上都写有数字2的概率是 .
14.如图,已知∠ADE=∠C,且AD=3,AF=8,AC=6,则AE= .
15.如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有 (填序号).
①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.
三、解答题
16.如图,已知 ∥ , .求证: .
17.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.
(1)在图①中,求∠AFB的度数;
(2)在图②中,∠AFB的度数为,图③中,∠AFB的度数为;
(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.
18.一个不透明的袋子里装有编号分别为1、2、3的球(除编号以为,其余都相同),其中1号球1个,3号球3个,从中随机摸出一个球是2号球的概率为.
(1)求袋子里2号球的个数.
(2)甲、乙两人分别从袋中摸出一个球(不放回),甲摸出球的编号记为x,乙摸出球的编号记为y,用列表法求点A(x,y)在直线y=x下方的概率.
19.老王准备给小陈打电话,由于保管不善,电话本上小陈的手机号码中有两个数字已模糊不清.如果用x,y表示这两个看不清的数字,那么小陈的手机号码为139x370y580(手机号码由11个数字组成),老王记得这11个数之和是20的整数倍.
(1) 求x+y的值.
(2)求老王一次拨对小陈手机号码的概率.
20.小颖和小丽做“摸球”游戏:在一个不透明的袋子中装有编号为1-4的四个球(除编号不同外其它都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字.若两次数字之和大于5,则小颖胜,否则小丽胜.这个游戏对双方公平吗?请说明理由.
21.如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.
22.在不透明的袋子中装有3个红球和5个黄球,每个球除颜色外都相同,从中任意摸出一个球
(1)摸到哪种颜色球的可能性大?
(2)请你通过改变袋子中某一种颜色球的数量,设计一种方案;使“摸出红球”和“摸出黄球”的可能性大小相同.
23.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)求BE的长;(2)求△ACD外接圆的半径.
一、单选题
1.在一个不透明的塑料袋中装有红色、白色球共40个,除颜色外其它都相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能( )
A.4个 B.6个 C.34个 D.36个
2.如图,点A,B,C在 上,四边形 是平行四边形.若对角线 ,则 的长为( )
A. B. C. D.
3.如图,是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
A. B.
C. D.
4.如图,在中,AC=BC=8,∠C=90°,以A点为圆心,AC长为半径作圆弧交AB 于E,连接CE,再分别以C、E为圆心,大于的长度为半径作弧,两弧交于点P,作射线AP交BC与点D,连接DE,则下列说法中不正确的是( )
A. B.
C. D.
5.如图,直线y=x+6分别与x轴、y轴相交于点M,N,∠MPN=90°,点C(0,3),则PC长度的最小值是( )
A.3 3 B.3﹣2 C. D.3
6.如图,在平面直角坐标系中,抛物线经过点,对称轴为直线.若,则x的取值范围是( )
A. B.
C. D.或
7.如图,将绕着点逆时针旋转,得到,若,,则的度数为( )
A. B. C. D.
8.若关于x的不等式组有解,则函数y=(a 3)x2 x 图象与x轴的交点个数为( )
A.0 B.1 C.2 D.1或2
9.如图,在国旗台DF上有一根旗杆AF,国庆节当天小明参加升旗仪式,在B处测得旗杆顶端的仰角为37°,小明向前走4米到达点E,经过坡度为1的坡面DE,坡面的水平距离是1米,到达点D,测得此时旗杆顶端的仰角为53°,则旗杆的高度约为( )米.(参考数据: , , )
A.6.29 B.4.71 C.4 D.5.33
10.已知二次函数的图象经过与两点,关于的一元二次方程有两个不同的实数根,其中一个根是如果关于的方程有两个不同的整数,则这两个整数根可能是( )
A., B.,
C., D.,
二、填空题
11.在2,-2,0三个整数中,任取一个,恰好使分式 有意义的概率是 。
12.如图,矩形ABCD是由两个边长为1的小正方形拼成,图中阴影部分是以B、D为圆心半径为1的两个小扇形,则这两个阴影部分面积之和为 .
13.甲、乙两个袋子中各装有2个相同的小球,分别写有数字1和2.从两个袋子中各随机取出1个小球,球上都写有数字2的概率是 .
14.如图,已知∠ADE=∠C,且AD=3,AF=8,AC=6,则AE= .
15.如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有 (填序号).
①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.
三、解答题
16.如图,已知 ∥ , .求证: .
17.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.
(1)在图①中,求∠AFB的度数;
(2)在图②中,∠AFB的度数为,图③中,∠AFB的度数为;
(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.
18.一个不透明的袋子里装有编号分别为1、2、3的球(除编号以为,其余都相同),其中1号球1个,3号球3个,从中随机摸出一个球是2号球的概率为.
(1)求袋子里2号球的个数.
(2)甲、乙两人分别从袋中摸出一个球(不放回),甲摸出球的编号记为x,乙摸出球的编号记为y,用列表法求点A(x,y)在直线y=x下方的概率.
19.老王准备给小陈打电话,由于保管不善,电话本上小陈的手机号码中有两个数字已模糊不清.如果用x,y表示这两个看不清的数字,那么小陈的手机号码为139x370y580(手机号码由11个数字组成),老王记得这11个数之和是20的整数倍.
(1) 求x+y的值.
(2)求老王一次拨对小陈手机号码的概率.
20.小颖和小丽做“摸球”游戏:在一个不透明的袋子中装有编号为1-4的四个球(除编号不同外其它都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字.若两次数字之和大于5,则小颖胜,否则小丽胜.这个游戏对双方公平吗?请说明理由.
21.如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.
22.在不透明的袋子中装有3个红球和5个黄球,每个球除颜色外都相同,从中任意摸出一个球
(1)摸到哪种颜色球的可能性大?
(2)请你通过改变袋子中某一种颜色球的数量,设计一种方案;使“摸出红球”和“摸出黄球”的可能性大小相同.
23.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)求BE的长;(2)求△ACD外接圆的半径.
同课章节目录
