2.5.1 直线与圆的位置关系 课件(共26张PPT)
文档属性
| 名称 | 2.5.1 直线与圆的位置关系 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 836.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 16:43:46 | ||
图片预览








文档简介
(共26张PPT)
2.5.1 直线与圆的
位置关系
2.5 直线与圆、
圆与圆的位置关系
人教A版
选择性必修第一册
图a
图b
图c
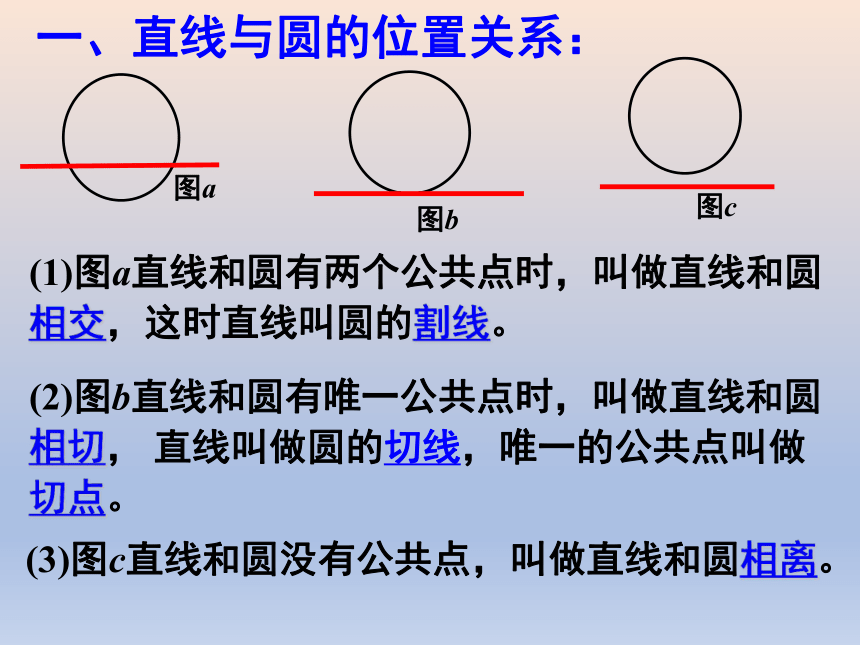
(2)图b直线和圆有唯一公共点时,叫做直线和圆相切, 直线叫做圆的切线,唯一的公共点叫做
切点。
(3)图c直线和圆没有公共点,叫做直线和圆相离。
(1)图a直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫圆的割线。
一、直线与圆的位置关系:
(3)直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系为______
相交
(1)直线x+y-2=0与圆x2+y2=2的位置关系为________
相切
(2)直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为_______
相离
(4)点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系为______
相交
1.填空题
几何法:
弦心距d
半径r
半弦
构成直角三角形的三边
三、弦长问题:
3. 已知直线y=x+1与圆 相交于A,B两点,求弦长|AB|的值.
【解析】设圆心O(0,0)到直线的距离为d,则
【分析】
(2)求过圆上一点的切线方程;
(3)求过圆外一点的切线方程;
(1)已知斜率,求圆的切线方程;
四、切线问题:
(4)求切线长.
10.已知圆C:(x+3)2+(y-4)2=25
(1)求斜率为1的圆C的切线方程;
(2)求过点P(1,1)的圆C的切线方程;
(3)求过点M(0,-1)的圆C的切线方程;
(4)求过点N(2,-3)的圆C的切线方程,并求切线长.
x0x+y0y=r2.
(x0-a)(x-a)+(y0-b)(y-b)=r2.
11.已知圆C:(x-3)2+(y-4)2=4,直线l:y=-x-1
(1)由直线l上的一点P向圆C引切线,求切线长的最小值;(2)点P在直线l上,直线PA、PB与圆C分别切于A、B两点,求四边形PACB面积的最小值.
【方法总结】
(1)形如 型的最值问题,可转化为过点(a,b)和点(x,y)的直线的斜率的最值问题.
(2)形如t=ax+by型的最值问题,可转化为动直线的截距的最值问题.
(3)形如u=(x-a)2+(y-b)2型的最值问题,可转化为动点到定点的距离平方的最值问题.
自 测
自 评
3
4
1
2
2.5.1 直线与圆的
位置关系
2.5 直线与圆、
圆与圆的位置关系
人教A版
选择性必修第一册
图a
图b
图c
(2)图b直线和圆有唯一公共点时,叫做直线和圆相切, 直线叫做圆的切线,唯一的公共点叫做
切点。
(3)图c直线和圆没有公共点,叫做直线和圆相离。
(1)图a直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫圆的割线。
一、直线与圆的位置关系:
(3)直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系为______
相交
(1)直线x+y-2=0与圆x2+y2=2的位置关系为________
相切
(2)直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为_______
相离
(4)点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系为______
相交
1.填空题
几何法:
弦心距d
半径r
半弦
构成直角三角形的三边
三、弦长问题:
3. 已知直线y=x+1与圆 相交于A,B两点,求弦长|AB|的值.
【解析】设圆心O(0,0)到直线的距离为d,则
【分析】
(2)求过圆上一点的切线方程;
(3)求过圆外一点的切线方程;
(1)已知斜率,求圆的切线方程;
四、切线问题:
(4)求切线长.
10.已知圆C:(x+3)2+(y-4)2=25
(1)求斜率为1的圆C的切线方程;
(2)求过点P(1,1)的圆C的切线方程;
(3)求过点M(0,-1)的圆C的切线方程;
(4)求过点N(2,-3)的圆C的切线方程,并求切线长.
x0x+y0y=r2.
(x0-a)(x-a)+(y0-b)(y-b)=r2.
11.已知圆C:(x-3)2+(y-4)2=4,直线l:y=-x-1
(1)由直线l上的一点P向圆C引切线,求切线长的最小值;(2)点P在直线l上,直线PA、PB与圆C分别切于A、B两点,求四边形PACB面积的最小值.
【方法总结】
(1)形如 型的最值问题,可转化为过点(a,b)和点(x,y)的直线的斜率的最值问题.
(2)形如t=ax+by型的最值问题,可转化为动直线的截距的最值问题.
(3)形如u=(x-a)2+(y-b)2型的最值问题,可转化为动点到定点的距离平方的最值问题.
自 测
自 评
3
4
1
2
