四川省泸州市重点中学2023-2024学年高一上学期12月月考数学试题(含答案)
文档属性
| 名称 | 四川省泸州市重点中学2023-2024学年高一上学期12月月考数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 881.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 19:05:46 | ||
图片预览



文档简介
泸州市重点中学2023级高一上期12月月考
数学试题
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.第I卷1至2页,第II卷3至4页.共150分.考试时间120分钟.
注意事项:
1.答题前,先将自己的姓名 准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题作答:每小题选出答案后,用2B铅笔把答题卡上对应题的答案标号涂黑.
3.填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内,作图题可先用铅笔绘出,确认后再用0.5毫米黑色签字笔描清楚,写在试题卷 草稿纸和答题卡上的非答题区域均无效.
4.考试结束后,请将本试题卷和答题卡一并上交.
第I卷(选择题共60分)
一 单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.化为角度是( )
A. B. C. D.
2.不等式的解集为( )
А. B. C. D.
3.若全集,集合及其关系用韦恩图表示如图,则图中阴影表示为( )
A. B.
C. D.
4.已知幂函数图象过点,则等于( )
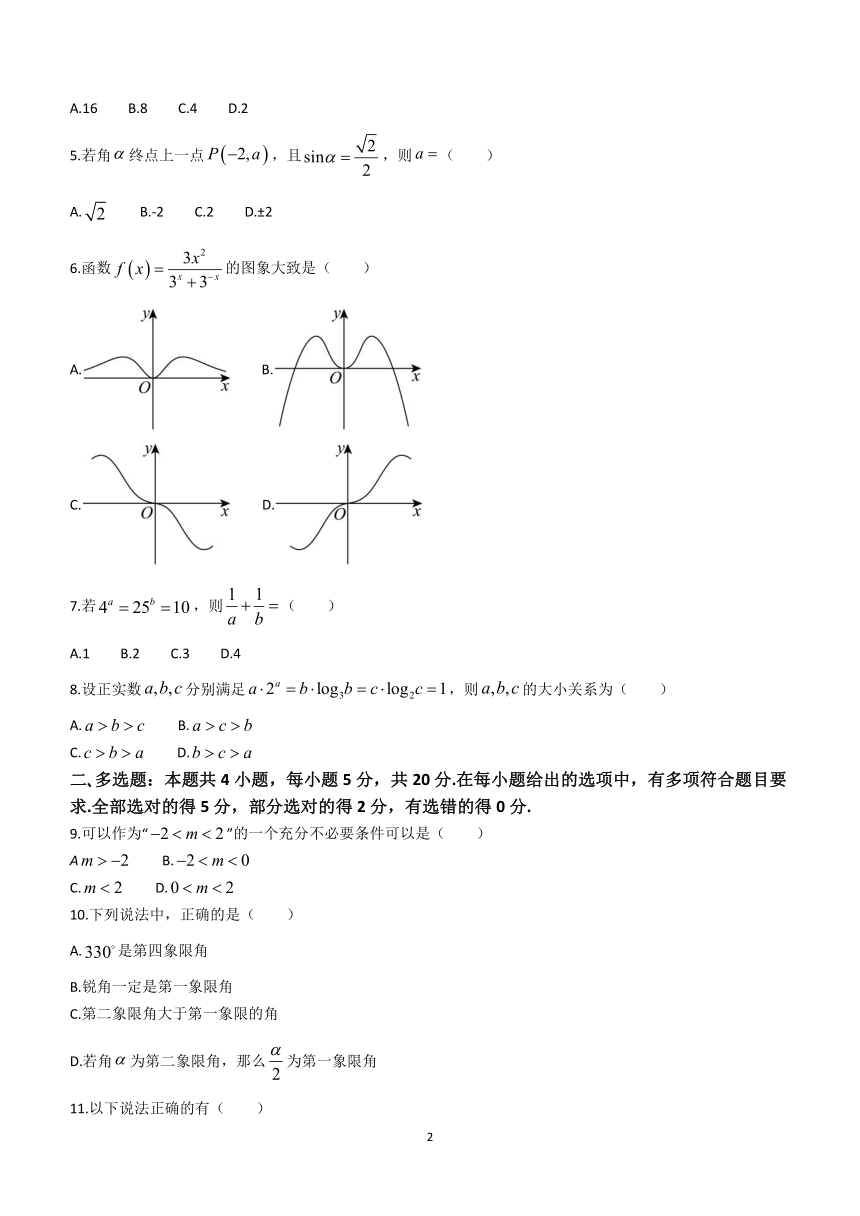
A.16 B.8 C.4 D.2
5.若角终点上一点,且,则( )
A. B.-2 C.2 D.±2
6.函数的图象大致是( )
A. B.
C. D.
7.若,则( )
A.1 B.2 C.3 D.4
8.设正实数分别满足,则的大小关系为( )
A. B.
C. D.
二 多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.可以作为“”的一个充分不必要条件可以是( )
A B.
C. D.
10.下列说法中,正确的是( )
A.是第四象限角
B.锐角一定是第一象限角
C.第二象限角大于第一象限的角
D.若角为第二象限角,那么为第一象限角
11.以下说法正确的有( )
A.实数是成立的充要条件
B.对恒成立
.命题“,使得”的否定是“,使得”
D.若,则的最小值是8
12.函数,下列结论正确的是( )
A.对任意成立
B.函数的值域是
C.若,则一定有
D.函数在上有1个零点
第II卷(非选择题共90分)
注意事项:
1.非选择题的答案必须用0.5毫米黑色签字笔直接答在答题卡上,作图题可先用铅笔绘出,确认后再用0.5毫米黑色签字笔描清楚,答在试题卷和草稿纸上无效.
2.本部分共10个小题,共90分.
三 填空题:本题共4小题,每小题5分,共20分.
13.已知函数的图象恒过定点__________.
14.已知,则__________.
15.沈照的《梦溪笔谈》是中国科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以为圆心为半径的圆弧,是的中点,在上,且.记的弧长的近似值为,“会圆术”给出了的一种计算公式:.若,,则根据该公式计算__________.
16.已知函数对任意两个不相等的实数,都满足不等式,则实数的取值范围是__________.
四 解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
(1);
(2).
18.(本小题满分12分)
设集合,函数的定义域为集合
(1)当时,求;
(2)若,求的取值范围.
19.(本小题满分12分)
(1)已知,求的值;
(2)已知,求的值.
20.(本小题满分12分)
(1)关于的不等式.若不等式的解集为,求的值;
(2)若,求不等式解集.
21.(本小题满分12分)
在国家大力发展新能源汽车产业政策影响下,我国新能源汽车的产销量高速增长.某地区2019年底新能源汽车保有量为1500辆,2020年底新能源汽车保有量为2250辆,2021年底新能源汽车保有量为3375辆.
(1)根据以上数据,试从且和且两种函数模型中选择一个最恰当的模型来刻画新能源汽车保有量的增长趋势并说明理由,设从2019年底起经过年后新能源汽车保有量为辆,求出新能源汽车保有量关于的函数关系式;
(2)2019年底该地区传统能源汽车保有量为50000辆,且传统能源汽车保有量每年下降,若每年新能源汽车保有量按(1)中求得的函数模型增长,试估计到哪一年底新能源汽车保有量将超过传统能源汽车保有量.(参考数据:)
22.(本小题满分12分)
已知函数且是偶函数.
(1)求的值;
(2)判断函数在的单调性,并用定义证明;
(3)若,且对有解,求的取值范围.
2023年秋期高一12月月考数学
参考答案
一 单选题:
题号 1 2 3 4 5 6 7 8
选项 B A C D C A B D
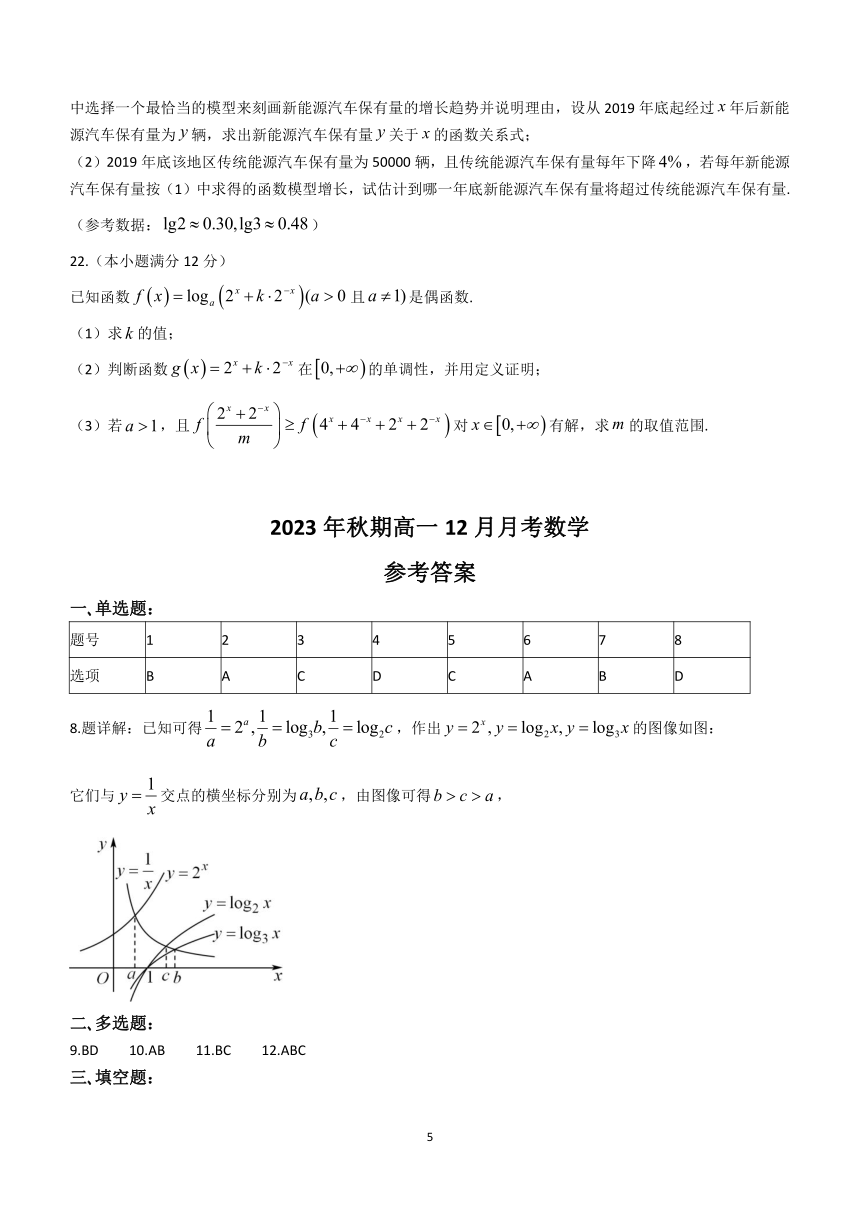
8.题详解:已知可得,作出的图像如图:
它们与交点的横坐标分别为,由图像可得,
二 多选题:
9.BD 10.AB 11.BC 12.ABC
三 填空题:
13.【答案】
14.【详解】由于,所以.
15.【答案】
【详解】如图,连接,
因为是的中点,所以,
又,所以三点共线,即,
又,所以,
则,故,
所以.
16.【详解】由可知,在上单调递减,
又因为在上单调递增,则在上单调递减,
且在上恒成立,所以,解得.
四 解答题
17.解(1)原式.
(2)原式.
18.解:(1)因为,所以,
则
当时,,所以
(2)当,即时,,满足.
当时,要使,则需,解得.
综上所述,的取值范围是.
19.【详解】(1)由,所以;
(2)由,可得,
即,则或,
当时,,则;
当时,,则;
所以或.
20.(1)解:原不等式可化为,
由题知,是方程的两根,由韦达定理得
解得
(2)解:当时,所以原不等式化为,
当时,即时,解原不等式可得或;
当时,即时,原不等式即为,解得;
当时,即时,解得或
综上所述,当时,解原不等式解集为:或;
当时,原不等式解集为;
当时,解得或
21.【详解】(1)由于新能源汽车保有量每年增长得越来越快,因此应该选择指数模型,应选函数模型是且,
由题意得得所以;
(2)设从2019年底起经过年后传统能源汽车保有量为辆,则有,设从2019年底起经过年后新能源汽车的数量将超过传统能源汽车,
则有,
即,即
两边同时取对数,得,解得,
故从2019年底起经过8年后,即2027年底新能源汽车的数量将超过传统能源汽车.
22.解:(1)因为函数且是偶函数,
所以,即,所以,
所以,因为不一定为零,所以
(2)由(1)得,则在上单调递增,理由如下:
任取,且,则
,
因为,且,所以,所以,
所以,即,
所以在上单调递增;
(3)当时,因为在上单调递增,
所以在上单调递增,
因为为偶函数,所以由,
则,
即
令,则,所以,所以在时有解,
所以,令,
在上单调递增,则
所以,所以,且,
所以且,即的取值范围为.
数学试题
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.第I卷1至2页,第II卷3至4页.共150分.考试时间120分钟.
注意事项:
1.答题前,先将自己的姓名 准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题作答:每小题选出答案后,用2B铅笔把答题卡上对应题的答案标号涂黑.
3.填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内,作图题可先用铅笔绘出,确认后再用0.5毫米黑色签字笔描清楚,写在试题卷 草稿纸和答题卡上的非答题区域均无效.
4.考试结束后,请将本试题卷和答题卡一并上交.
第I卷(选择题共60分)
一 单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.化为角度是( )
A. B. C. D.
2.不等式的解集为( )
А. B. C. D.
3.若全集,集合及其关系用韦恩图表示如图,则图中阴影表示为( )
A. B.
C. D.
4.已知幂函数图象过点,则等于( )
A.16 B.8 C.4 D.2
5.若角终点上一点,且,则( )
A. B.-2 C.2 D.±2
6.函数的图象大致是( )
A. B.
C. D.
7.若,则( )
A.1 B.2 C.3 D.4
8.设正实数分别满足,则的大小关系为( )
A. B.
C. D.
二 多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.可以作为“”的一个充分不必要条件可以是( )
A B.
C. D.
10.下列说法中,正确的是( )
A.是第四象限角
B.锐角一定是第一象限角
C.第二象限角大于第一象限的角
D.若角为第二象限角,那么为第一象限角
11.以下说法正确的有( )
A.实数是成立的充要条件
B.对恒成立
.命题“,使得”的否定是“,使得”
D.若,则的最小值是8
12.函数,下列结论正确的是( )
A.对任意成立
B.函数的值域是
C.若,则一定有
D.函数在上有1个零点
第II卷(非选择题共90分)
注意事项:
1.非选择题的答案必须用0.5毫米黑色签字笔直接答在答题卡上,作图题可先用铅笔绘出,确认后再用0.5毫米黑色签字笔描清楚,答在试题卷和草稿纸上无效.
2.本部分共10个小题,共90分.
三 填空题:本题共4小题,每小题5分,共20分.
13.已知函数的图象恒过定点__________.
14.已知,则__________.
15.沈照的《梦溪笔谈》是中国科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以为圆心为半径的圆弧,是的中点,在上,且.记的弧长的近似值为,“会圆术”给出了的一种计算公式:.若,,则根据该公式计算__________.
16.已知函数对任意两个不相等的实数,都满足不等式,则实数的取值范围是__________.
四 解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
(1);
(2).
18.(本小题满分12分)
设集合,函数的定义域为集合
(1)当时,求;
(2)若,求的取值范围.
19.(本小题满分12分)
(1)已知,求的值;
(2)已知,求的值.
20.(本小题满分12分)
(1)关于的不等式.若不等式的解集为,求的值;
(2)若,求不等式解集.
21.(本小题满分12分)
在国家大力发展新能源汽车产业政策影响下,我国新能源汽车的产销量高速增长.某地区2019年底新能源汽车保有量为1500辆,2020年底新能源汽车保有量为2250辆,2021年底新能源汽车保有量为3375辆.
(1)根据以上数据,试从且和且两种函数模型中选择一个最恰当的模型来刻画新能源汽车保有量的增长趋势并说明理由,设从2019年底起经过年后新能源汽车保有量为辆,求出新能源汽车保有量关于的函数关系式;
(2)2019年底该地区传统能源汽车保有量为50000辆,且传统能源汽车保有量每年下降,若每年新能源汽车保有量按(1)中求得的函数模型增长,试估计到哪一年底新能源汽车保有量将超过传统能源汽车保有量.(参考数据:)
22.(本小题满分12分)
已知函数且是偶函数.
(1)求的值;
(2)判断函数在的单调性,并用定义证明;
(3)若,且对有解,求的取值范围.
2023年秋期高一12月月考数学
参考答案
一 单选题:
题号 1 2 3 4 5 6 7 8
选项 B A C D C A B D
8.题详解:已知可得,作出的图像如图:
它们与交点的横坐标分别为,由图像可得,
二 多选题:
9.BD 10.AB 11.BC 12.ABC
三 填空题:
13.【答案】
14.【详解】由于,所以.
15.【答案】
【详解】如图,连接,
因为是的中点,所以,
又,所以三点共线,即,
又,所以,
则,故,
所以.
16.【详解】由可知,在上单调递减,
又因为在上单调递增,则在上单调递减,
且在上恒成立,所以,解得.
四 解答题
17.解(1)原式.
(2)原式.
18.解:(1)因为,所以,
则
当时,,所以
(2)当,即时,,满足.
当时,要使,则需,解得.
综上所述,的取值范围是.
19.【详解】(1)由,所以;
(2)由,可得,
即,则或,
当时,,则;
当时,,则;
所以或.
20.(1)解:原不等式可化为,
由题知,是方程的两根,由韦达定理得
解得
(2)解:当时,所以原不等式化为,
当时,即时,解原不等式可得或;
当时,即时,原不等式即为,解得;
当时,即时,解得或
综上所述,当时,解原不等式解集为:或;
当时,原不等式解集为;
当时,解得或
21.【详解】(1)由于新能源汽车保有量每年增长得越来越快,因此应该选择指数模型,应选函数模型是且,
由题意得得所以;
(2)设从2019年底起经过年后传统能源汽车保有量为辆,则有,设从2019年底起经过年后新能源汽车的数量将超过传统能源汽车,
则有,
即,即
两边同时取对数,得,解得,
故从2019年底起经过8年后,即2027年底新能源汽车的数量将超过传统能源汽车.
22.解:(1)因为函数且是偶函数,
所以,即,所以,
所以,因为不一定为零,所以
(2)由(1)得,则在上单调递增,理由如下:
任取,且,则
,
因为,且,所以,所以,
所以,即,
所以在上单调递增;
(3)当时,因为在上单调递增,
所以在上单调递增,
因为为偶函数,所以由,
则,
即
令,则,所以,所以在时有解,
所以,令,
在上单调递增,则
所以,所以,且,
所以且,即的取值范围为.
同课章节目录
