江苏省南京市江宁区2023-2024学年九年级上学期12月月考数学试题(含答案)
文档属性
| 名称 | 江苏省南京市江宁区2023-2024学年九年级上学期12月月考数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-31 19:56:02 | ||
图片预览




文档简介
九年级数学第二次学科素养限时作业 2023.12
(总分120分 时间120分钟)
【注意】:本卷所有解答均写在答题卡相应位置上
一.选择题(每题2分,共12分)
1.下列函数是二次函数的是( )
A. B. C. D.
2.已知点是线段的黄金分割点,若,则的长约为( )
A.0.382 B.3.82 C.0.618 D.6.18
3.在一个不透明的袋中装有5个球,其中2个红球,3个白球,这些球除颜色外无其他差别,从中随机摸出1个球,摸出红球的概率是( )
A. B. C. D.
4.将二次函数的图象先向下平移1个单位,再向右平移2个单位,则平移后的二次函数的解析式为( )
A. B. C. D.
5.如图是二次函数的图象,则不等式的解集是( )
第5题
A. B.或 C. D.或
6.如图,以线段为边分别作直角三角形和等边三角形,其中.连接,当的长度最大时,此时的大小是( )
第6题
A. B. C. D.
二、填空题(每题2分,共20分)
7.若,则______.
8.设,是关于的方程的两个根,且,则的值为______.
9.某公司一月份的产值为200万元,二,三月份的产值总和为720万元,设公司每月产值的平均增长率为,则可列方程为_______.
10.用一个圆心角为,半径为12的扇形作一个圆雉的侧面,则这个圆雉的底面半径为______.
11.已知,若的三边分别长为6、8、10,的面积为96,则的周长为_______.
12.已知二次函数中,函数与自变量的部分对应值如表所示:
… -5 -4 -3 -2 -1 …
… -8 -3 0 1 0 …
当时,的取值范围是______.
13.如图,在边长为1的正方形网格中,A、B、C、D为格点,连接AB、CD相交于点E,则AE的长为______.
第13题
14.如图,内接于,外角的平分线交于点D,射线AD交CB延长线于点E.若
,,则的度数为______.
第14题图
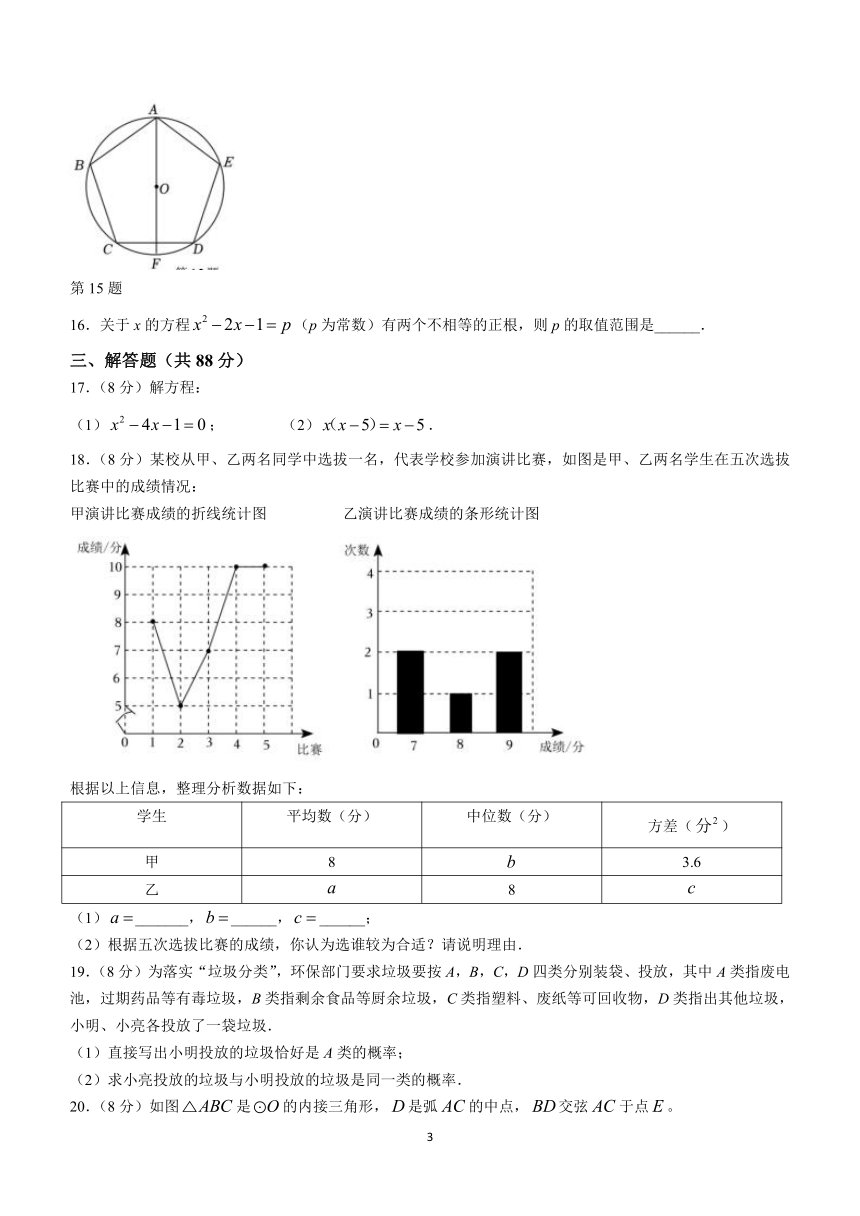
15.如图,正五边形ABCDE内接于⊙O,AF是⊙O的直径,P是⊙O上的一点(不与点B,F重合),则
∠BPF的度数为_______.
第15题
16.关于x的方程(p为常数)有两个不相等的正根,则p的取值范围是______.
三、解答题(共88分)
17.(8分)解方程:
(1); (2).
18.(8分)某校从甲、乙两名同学中选拔一名,代表学校参加演讲比赛,如图是甲、乙两名学生在五次选拔比赛中的成绩情况:
甲演讲比赛成绩的折线统计图 乙演讲比赛成绩的条形统计图
根据以上信息,整理分析数据如下:
学生 平均数(分) 中位数(分) 方差()
甲 8 3.6
乙 8
(1)_______,______,______;
(2)根据五次选拔比赛的成绩,你认为选谁较为合适?请说明理由.
19.(8分)为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率;
(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.
20.(8分)如图是的内接三角形,是弧的中点,交弦于点。
(1)求证:;
(2)若,,求的长.
21.(8分)已知二次函数(为常数).
(1)求证:不论为何值,该函数的图象与轴总有两个公共点;
(2)若函数的图象与轴的两个公共点分别在原点的两侧,求的取值范围.
22.(10分)已知二次函数的函数值与自变量的部分对应值如下表:
… -2 -1 0 1 2 3 …
… 10 0 -6 -8 -6 0 …
(1)求该二次函数的表达式;
(2)当时,的取值范围是______.
(3)该图像关于轴对称的函数图像的表达式为______.
23.(8分)如图,是的直径,射线交交于点.
(1)尺规作图:求作的中点.(保留作图痕迹)
(2)过点画垂足为.若,,求的面积.
24.(8分)如图,点为正方形的边上的一点,是的外接圆,与交于点,是上一点,且.
(1)求证:是的切线;
(2)若,,求半径的长.
25.(10分)某超市销售一种饮料,每瓶进价为9元,当每瓶售价为10元时,日均销售量为560瓶.经市场调查表明,每瓶售价每增加0.5元,日均销售量减少40瓶.
(1)当每 售价为11元时,日均销售量为______瓶;
(2)当每 售价为多少元时,所得日均总利润最大?最大日均总利润为多少元?
26.(12分)如图,在矩形中,,,动点在边上以每秒的速度由点向点运动,设动点运动的时间为,连接,过点作交边于点,延长至点,使得,连接,.
(1)当点由点运动到点时,点运动的路程为______;
(2)设的面积为,的面积为,求,与的函数表达式,并写出自变量的取值范围;
(3)当所在直线经过中点时,求的值.
备用图
数学参考答案
一.选择题(每题2分,共12分)
1.C 2.B 3.A 4.C 5.D 6.A
二、填空题(每题2分,共20分)
7. 8.0
9. 10.5 11.48
12. 13. 14.40 15.54或126 16.
三、解答题(共64分)
17.(1), (2),
18.(8分)(1)8,8,0.8;
(2)乙.可从平均数、中位数、方差来分析。(2分一空)
19.(1)(2分)垃圾要按A,B,C,D四类分别装袋,小明投放了一袋垃圾,
小明投放的垃圾恰好是A类的概率为:;
(2)(6分)如图所示:
由图可知,共有16种等可能结果,其中小亮投放的垃圾与小明投放的垃圾是同一类的结果有4种,所以小亮投放的垃圾与小明投放的垃圾是同一类的概率为.(方法不唯一 可直接列举所有等可能结果。16种结果列对给3分)
20.(8分)
(1)证明:是的中点,
,,,
.(4分)
(2)解:,
, ,,
,,,
解得或(不符合题意,舍去),
的长是2.(4分)
21.(8分)
(1)令,.
因为,
所以方程有两个不相等的实数根.
所以该函数图像与轴总有两个公共点.
证法二:
当时,.
解这个方程,得,.
因为,所以方程有两个不相等的实数根.
所以该函数图像与轴总有两个公共点.
(2)解:当时,.解这个方程,得,.
函数图像与轴的交点的坐标为,.
因为函数图像与轴的两个公共点分别在原点的两侧,且,
所以且.解得.
22.(1)(4分)
(2)(2分)
(3)(2分)
23.(1)(方法不唯一)(4分)
(2)是的直径,,
,,,
,,
四边形为矩形,,
,
在中,,
的面积.(4分)
24.证明:(1)连接,
,
,
四边形是正方形,
,
,
,,
四边形是正方形,
,,
,
,,
点是上的一点,
是的切线;
(2)解:连接,
是的外接圆,,
是的直径,
,
四边形是正方形,
,
四边形是矩形,
,
,,
,
,
四边形是正方形,
,,,
,
.
25.(1)当每瓶的售价为11元时,日均销售量为瓶,故答案为:480;(2分)
(2)设每瓶的售价为元,日均利润为元,
则
,
当时,取得最大值,最大值为1280,
答:当每瓶售价为13元时,所得日均总利润最大,最大日均总利润为1280元.(6分)
26.(1)四边形为矩形,
,
,
,,
,,
,即,
解得,,
当时,有最大值4,
点运动的路程为:,
故答案为:8;(3分)
(2)如图1,过点作交的延长线于交的延长线于,
,,,,,,即,
解得,,,
则,
,
;(5分)
(3)点是的中点,
,,
,,
解得,,(不合题意,舍去),
当所在直线经过中点时,的值为.(4分)
图1
(总分120分 时间120分钟)
【注意】:本卷所有解答均写在答题卡相应位置上
一.选择题(每题2分,共12分)
1.下列函数是二次函数的是( )
A. B. C. D.
2.已知点是线段的黄金分割点,若,则的长约为( )
A.0.382 B.3.82 C.0.618 D.6.18
3.在一个不透明的袋中装有5个球,其中2个红球,3个白球,这些球除颜色外无其他差别,从中随机摸出1个球,摸出红球的概率是( )
A. B. C. D.
4.将二次函数的图象先向下平移1个单位,再向右平移2个单位,则平移后的二次函数的解析式为( )
A. B. C. D.
5.如图是二次函数的图象,则不等式的解集是( )
第5题
A. B.或 C. D.或
6.如图,以线段为边分别作直角三角形和等边三角形,其中.连接,当的长度最大时,此时的大小是( )
第6题
A. B. C. D.
二、填空题(每题2分,共20分)
7.若,则______.
8.设,是关于的方程的两个根,且,则的值为______.
9.某公司一月份的产值为200万元,二,三月份的产值总和为720万元,设公司每月产值的平均增长率为,则可列方程为_______.
10.用一个圆心角为,半径为12的扇形作一个圆雉的侧面,则这个圆雉的底面半径为______.
11.已知,若的三边分别长为6、8、10,的面积为96,则的周长为_______.
12.已知二次函数中,函数与自变量的部分对应值如表所示:
… -5 -4 -3 -2 -1 …
… -8 -3 0 1 0 …
当时,的取值范围是______.
13.如图,在边长为1的正方形网格中,A、B、C、D为格点,连接AB、CD相交于点E,则AE的长为______.
第13题
14.如图,内接于,外角的平分线交于点D,射线AD交CB延长线于点E.若
,,则的度数为______.
第14题图
15.如图,正五边形ABCDE内接于⊙O,AF是⊙O的直径,P是⊙O上的一点(不与点B,F重合),则
∠BPF的度数为_______.
第15题
16.关于x的方程(p为常数)有两个不相等的正根,则p的取值范围是______.
三、解答题(共88分)
17.(8分)解方程:
(1); (2).
18.(8分)某校从甲、乙两名同学中选拔一名,代表学校参加演讲比赛,如图是甲、乙两名学生在五次选拔比赛中的成绩情况:
甲演讲比赛成绩的折线统计图 乙演讲比赛成绩的条形统计图
根据以上信息,整理分析数据如下:
学生 平均数(分) 中位数(分) 方差()
甲 8 3.6
乙 8
(1)_______,______,______;
(2)根据五次选拔比赛的成绩,你认为选谁较为合适?请说明理由.
19.(8分)为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率;
(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.
20.(8分)如图是的内接三角形,是弧的中点,交弦于点。
(1)求证:;
(2)若,,求的长.
21.(8分)已知二次函数(为常数).
(1)求证:不论为何值,该函数的图象与轴总有两个公共点;
(2)若函数的图象与轴的两个公共点分别在原点的两侧,求的取值范围.
22.(10分)已知二次函数的函数值与自变量的部分对应值如下表:
… -2 -1 0 1 2 3 …
… 10 0 -6 -8 -6 0 …
(1)求该二次函数的表达式;
(2)当时,的取值范围是______.
(3)该图像关于轴对称的函数图像的表达式为______.
23.(8分)如图,是的直径,射线交交于点.
(1)尺规作图:求作的中点.(保留作图痕迹)
(2)过点画垂足为.若,,求的面积.
24.(8分)如图,点为正方形的边上的一点,是的外接圆,与交于点,是上一点,且.
(1)求证:是的切线;
(2)若,,求半径的长.
25.(10分)某超市销售一种饮料,每瓶进价为9元,当每瓶售价为10元时,日均销售量为560瓶.经市场调查表明,每瓶售价每增加0.5元,日均销售量减少40瓶.
(1)当每 售价为11元时,日均销售量为______瓶;
(2)当每 售价为多少元时,所得日均总利润最大?最大日均总利润为多少元?
26.(12分)如图,在矩形中,,,动点在边上以每秒的速度由点向点运动,设动点运动的时间为,连接,过点作交边于点,延长至点,使得,连接,.
(1)当点由点运动到点时,点运动的路程为______;
(2)设的面积为,的面积为,求,与的函数表达式,并写出自变量的取值范围;
(3)当所在直线经过中点时,求的值.
备用图
数学参考答案
一.选择题(每题2分,共12分)
1.C 2.B 3.A 4.C 5.D 6.A
二、填空题(每题2分,共20分)
7. 8.0
9. 10.5 11.48
12. 13. 14.40 15.54或126 16.
三、解答题(共64分)
17.(1), (2),
18.(8分)(1)8,8,0.8;
(2)乙.可从平均数、中位数、方差来分析。(2分一空)
19.(1)(2分)垃圾要按A,B,C,D四类分别装袋,小明投放了一袋垃圾,
小明投放的垃圾恰好是A类的概率为:;
(2)(6分)如图所示:
由图可知,共有16种等可能结果,其中小亮投放的垃圾与小明投放的垃圾是同一类的结果有4种,所以小亮投放的垃圾与小明投放的垃圾是同一类的概率为.(方法不唯一 可直接列举所有等可能结果。16种结果列对给3分)
20.(8分)
(1)证明:是的中点,
,,,
.(4分)
(2)解:,
, ,,
,,,
解得或(不符合题意,舍去),
的长是2.(4分)
21.(8分)
(1)令,.
因为,
所以方程有两个不相等的实数根.
所以该函数图像与轴总有两个公共点.
证法二:
当时,.
解这个方程,得,.
因为,所以方程有两个不相等的实数根.
所以该函数图像与轴总有两个公共点.
(2)解:当时,.解这个方程,得,.
函数图像与轴的交点的坐标为,.
因为函数图像与轴的两个公共点分别在原点的两侧,且,
所以且.解得.
22.(1)(4分)
(2)(2分)
(3)(2分)
23.(1)(方法不唯一)(4分)
(2)是的直径,,
,,,
,,
四边形为矩形,,
,
在中,,
的面积.(4分)
24.证明:(1)连接,
,
,
四边形是正方形,
,
,
,,
四边形是正方形,
,,
,
,,
点是上的一点,
是的切线;
(2)解:连接,
是的外接圆,,
是的直径,
,
四边形是正方形,
,
四边形是矩形,
,
,,
,
,
四边形是正方形,
,,,
,
.
25.(1)当每瓶的售价为11元时,日均销售量为瓶,故答案为:480;(2分)
(2)设每瓶的售价为元,日均利润为元,
则
,
当时,取得最大值,最大值为1280,
答:当每瓶售价为13元时,所得日均总利润最大,最大日均总利润为1280元.(6分)
26.(1)四边形为矩形,
,
,
,,
,,
,即,
解得,,
当时,有最大值4,
点运动的路程为:,
故答案为:8;(3分)
(2)如图1,过点作交的延长线于交的延长线于,
,,,,,,即,
解得,,,
则,
,
;(5分)
(3)点是的中点,
,,
,,
解得,,(不合题意,舍去),
当所在直线经过中点时,的值为.(4分)
图1
同课章节目录
