29.1.2正投影 教案 2023-2024学年 人教版数学九年级下册
文档属性
| 名称 | 29.1.2正投影 教案 2023-2024学年 人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 169.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 10:57:09 | ||
图片预览


文档简介
29.1 投 影
第2课时 正投影
教学目标:
1.了解正投影的概念.能根据正投影的性质画出简单的平面图形的正投影.
2.通过动手操作画图形的正投影,培养学生动手实践能力,发展空间想象能力.
3.感受日常生活中的一些投影现象,体会数学与生活实际密不可分,激发学生学习数学的兴趣.
教学重难点:
重点:
1.正投影的含义.
2.能根据正投影的性质画出简单的平面图形的正投影.
难点:归纳正投影的性质,正确画出简单平面图形的正投影.
教学过程
导入
复习
1.说一说什么是投影、投影线、投影面
2.什么是平行投影和中心投影 它们有什么区别和联系
[师生活动] 学生思考后回答问题,小组内交流,回答,教师点评,导入新课.
新课讲授
知识点1 正投影的概念及性质
观察与思考
图中表示一块三角尺在光线照射下形成的投影,其中图(1)与图(2)(3)的投影线有什么区别 图(2)(3)的投影线与投影面的位置关系有什么区别
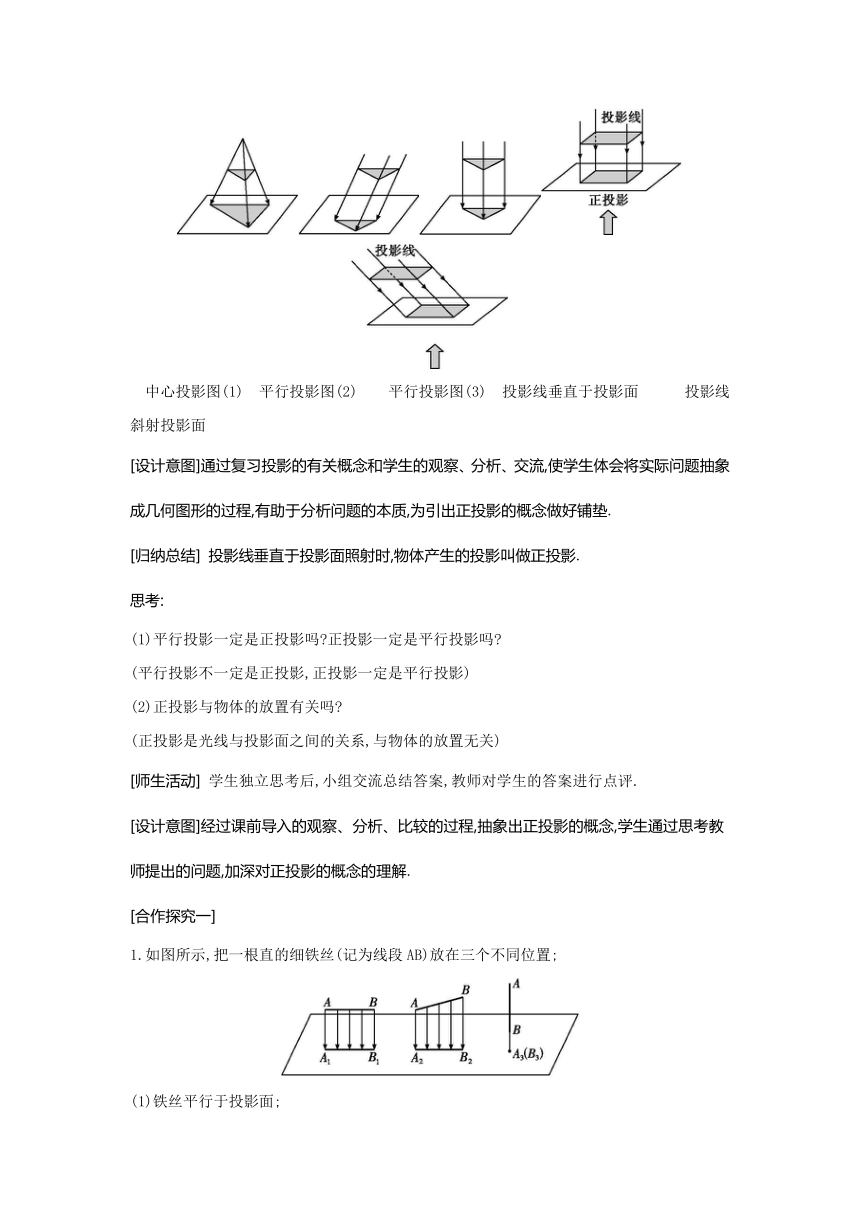
中心投影图(1) 平行投影图(2) 平行投影图(3) 投影线垂直于投影面 投影线斜射投影面
[设计意图]通过复习投影的有关概念和学生的观察、分析、交流,使学生体会将实际问题抽象成几何图形的过程,有助于分析问题的本质,为引出正投影的概念做好铺垫.
[归纳总结] 投影线垂直于投影面照射时,物体产生的投影叫做正投影.
思考:
(1)平行投影一定是正投影吗 正投影一定是平行投影吗
(平行投影不一定是正投影,正投影一定是平行投影)
(2)正投影与物体的放置有关吗
(正投影是光线与投影面之间的关系,与物体的放置无关)
[师生活动] 学生独立思考后,小组交流总结答案,教师对学生的答案进行点评.
[设计意图]经过课前导入的观察、分析、比较的过程,抽象出正投影的概念,学生通过思考教师提出的问题,加深对正投影的概念的理解.
[合作探究一]
1.如图所示,把一根直的细铁丝(记为线段AB)放在三个不同位置;
(1)铁丝平行于投影面;
(2)铁丝倾斜于投影面;
(3)铁丝垂直于投影面(铁丝不一定要与投影面有交点).
思考:三种情形下铁丝的正投影各是什么形状 大小有什么关系
[归纳] 通过观察,我们可以发现:
(1)当线段AB平行于投影面时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB=A1B1;
(2)当线段AB倾斜于投影面时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB>A2B2;
(3)当线段AB垂直于投影面时,它的正投影是一个点A3(B3).
[合作探究二]
2.如图所示,把一块正方形硬纸板ABCD放在三个不同位置:(1)纸板平行于投影面;(2)纸板倾斜于投影面;(3)纸板垂直于投影面.三种情形下纸板的正投影各是什么形状
思考:三种情形下纸板的正投影各是什么形状 大小有什么关系
[归纳] 通过观察、测量可知:
(1)当纸板平行于投影面时,纸板的正投影与纸板的形状、大小一样;
(2)当纸板倾斜于投影面时,纸板的正投影与纸板的形状、大小不完全一样;
(3)当纸板垂直于投影面时,纸板的正投影成为一条线段.
[归纳总结] 当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
知识点2 画几何体的正投影
画出如图所示摆放的正方体在投影面上的正投影.
(1)如图(1)所示,正方体的一个面ABCD平行于投影面;
(2)如图(2)所示,正方体的一个面ABCD倾斜于投影面,上底面ADEF垂直于投影面,并且上底面的对角线AE垂直于投影面.
解:(1)如图①所示,正方体的正投影为正方形A'B'C'D',它与正方体的一个面是全等关系.
(2)如图②所示,正方体的正投影为矩形F'G'C'D',这个矩形的长等于正方体的底面对角线长,矩形的宽等于正方体的棱长.矩形上、下两边中点连线A'B'是正方体的侧棱AB及它所对的另一条侧棱EH的投影.
范例应用
例1 几何体在平面内的正投影,取决于(A)
①几何体的形状;②几何体与投影面的位置关系;③投影面的大小.
A.①② B.①③ C.②③ D.①②③
[分析] 几何体的形状不同,其正投影一般也不同,所以①正确.几何体与投影面的位置关系不同,其正投影也不同,②正确.几何体在平面内的正投影与投影面的大小无关,所以③错误.
例2 画出下列立体图形的正投影(投影线从上方射向下方).
解:如图所示.
课堂训练
1.如图所示,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是(D)
2.如图所示,把正方体的一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光线垂直,则正方体在纸上的正投影是(C)
3.如图所示,正方形纸板ABCD边长为10 cm,四边形A'B'C'D'是正方形纸板ABCD在平面上的正投影,AD,BC与平面平行,AB,CD与平面成30°角,求四边形A'B'C'D'的面积.
解:如图所示,作AH⊥BB'于点H.则∠BAH=30°.
在Rt△ABH中,AH=AB·cos∠BAH=10·cos 30°=10×=5(cm).
所以根据正投影的性质知
A'B'=AH=5(cm),A'D'=AD=10 cm.
S四边形A'B'C'D'=A'B'·A'D'=5×10=50(cm2).
所以四边形A'B'C'D'的面积为50 cm2.
小结
正投影
1.正投影的概念及性质
2.平面图形的正投影
3.几何体的正投影
板书
第2课时 正投影
1.认识概念:正投影
2.探究性质
探究一:线段在平面上的正投影
探究二:正方形纸板在平面上的正投影
反思
本节课的重点是通过观察、思考及动手操作,抽象出正投影的概念和性质,培养学生空间想象能力和归纳总结能力,教学设计时,本以为影子是学生熟悉的生活情景,学生应该易于理解和掌握,所以在探究正投影的性质时,速度稍快些,结果有些学生缺乏空间想象能力,造成抽象概括其性质有困难,在以后的教学中,应注重培养学生空间想象及抽象概括能力,多给学生相互交流的时间和空间.
第2课时 正投影
教学目标:
1.了解正投影的概念.能根据正投影的性质画出简单的平面图形的正投影.
2.通过动手操作画图形的正投影,培养学生动手实践能力,发展空间想象能力.
3.感受日常生活中的一些投影现象,体会数学与生活实际密不可分,激发学生学习数学的兴趣.
教学重难点:
重点:
1.正投影的含义.
2.能根据正投影的性质画出简单的平面图形的正投影.
难点:归纳正投影的性质,正确画出简单平面图形的正投影.
教学过程
导入
复习
1.说一说什么是投影、投影线、投影面
2.什么是平行投影和中心投影 它们有什么区别和联系
[师生活动] 学生思考后回答问题,小组内交流,回答,教师点评,导入新课.
新课讲授
知识点1 正投影的概念及性质
观察与思考
图中表示一块三角尺在光线照射下形成的投影,其中图(1)与图(2)(3)的投影线有什么区别 图(2)(3)的投影线与投影面的位置关系有什么区别
中心投影图(1) 平行投影图(2) 平行投影图(3) 投影线垂直于投影面 投影线斜射投影面
[设计意图]通过复习投影的有关概念和学生的观察、分析、交流,使学生体会将实际问题抽象成几何图形的过程,有助于分析问题的本质,为引出正投影的概念做好铺垫.
[归纳总结] 投影线垂直于投影面照射时,物体产生的投影叫做正投影.
思考:
(1)平行投影一定是正投影吗 正投影一定是平行投影吗
(平行投影不一定是正投影,正投影一定是平行投影)
(2)正投影与物体的放置有关吗
(正投影是光线与投影面之间的关系,与物体的放置无关)
[师生活动] 学生独立思考后,小组交流总结答案,教师对学生的答案进行点评.
[设计意图]经过课前导入的观察、分析、比较的过程,抽象出正投影的概念,学生通过思考教师提出的问题,加深对正投影的概念的理解.
[合作探究一]
1.如图所示,把一根直的细铁丝(记为线段AB)放在三个不同位置;
(1)铁丝平行于投影面;
(2)铁丝倾斜于投影面;
(3)铁丝垂直于投影面(铁丝不一定要与投影面有交点).
思考:三种情形下铁丝的正投影各是什么形状 大小有什么关系
[归纳] 通过观察,我们可以发现:
(1)当线段AB平行于投影面时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB=A1B1;
(2)当线段AB倾斜于投影面时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB>A2B2;
(3)当线段AB垂直于投影面时,它的正投影是一个点A3(B3).
[合作探究二]
2.如图所示,把一块正方形硬纸板ABCD放在三个不同位置:(1)纸板平行于投影面;(2)纸板倾斜于投影面;(3)纸板垂直于投影面.三种情形下纸板的正投影各是什么形状
思考:三种情形下纸板的正投影各是什么形状 大小有什么关系
[归纳] 通过观察、测量可知:
(1)当纸板平行于投影面时,纸板的正投影与纸板的形状、大小一样;
(2)当纸板倾斜于投影面时,纸板的正投影与纸板的形状、大小不完全一样;
(3)当纸板垂直于投影面时,纸板的正投影成为一条线段.
[归纳总结] 当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
知识点2 画几何体的正投影
画出如图所示摆放的正方体在投影面上的正投影.
(1)如图(1)所示,正方体的一个面ABCD平行于投影面;
(2)如图(2)所示,正方体的一个面ABCD倾斜于投影面,上底面ADEF垂直于投影面,并且上底面的对角线AE垂直于投影面.
解:(1)如图①所示,正方体的正投影为正方形A'B'C'D',它与正方体的一个面是全等关系.
(2)如图②所示,正方体的正投影为矩形F'G'C'D',这个矩形的长等于正方体的底面对角线长,矩形的宽等于正方体的棱长.矩形上、下两边中点连线A'B'是正方体的侧棱AB及它所对的另一条侧棱EH的投影.
范例应用
例1 几何体在平面内的正投影,取决于(A)
①几何体的形状;②几何体与投影面的位置关系;③投影面的大小.
A.①② B.①③ C.②③ D.①②③
[分析] 几何体的形状不同,其正投影一般也不同,所以①正确.几何体与投影面的位置关系不同,其正投影也不同,②正确.几何体在平面内的正投影与投影面的大小无关,所以③错误.
例2 画出下列立体图形的正投影(投影线从上方射向下方).
解:如图所示.
课堂训练
1.如图所示,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是(D)
2.如图所示,把正方体的一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光线垂直,则正方体在纸上的正投影是(C)
3.如图所示,正方形纸板ABCD边长为10 cm,四边形A'B'C'D'是正方形纸板ABCD在平面上的正投影,AD,BC与平面平行,AB,CD与平面成30°角,求四边形A'B'C'D'的面积.
解:如图所示,作AH⊥BB'于点H.则∠BAH=30°.
在Rt△ABH中,AH=AB·cos∠BAH=10·cos 30°=10×=5(cm).
所以根据正投影的性质知
A'B'=AH=5(cm),A'D'=AD=10 cm.
S四边形A'B'C'D'=A'B'·A'D'=5×10=50(cm2).
所以四边形A'B'C'D'的面积为50 cm2.
小结
正投影
1.正投影的概念及性质
2.平面图形的正投影
3.几何体的正投影
板书
第2课时 正投影
1.认识概念:正投影
2.探究性质
探究一:线段在平面上的正投影
探究二:正方形纸板在平面上的正投影
反思
本节课的重点是通过观察、思考及动手操作,抽象出正投影的概念和性质,培养学生空间想象能力和归纳总结能力,教学设计时,本以为影子是学生熟悉的生活情景,学生应该易于理解和掌握,所以在探究正投影的性质时,速度稍快些,结果有些学生缺乏空间想象能力,造成抽象概括其性质有困难,在以后的教学中,应注重培养学生空间想象及抽象概括能力,多给学生相互交流的时间和空间.
