期末经典题型练习(二)2023-2024学年九年级上册苏科版(含解析)
文档属性
| 名称 | 期末经典题型练习(二)2023-2024学年九年级上册苏科版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 22:45:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末经典题型练习(二)2023-2024学年九年级上册苏科版
一、单选题
1.掷一枚质地均匀的骰子,骰子停止后,出现可能性大的是( )
A.小于3的点数 B.大于3的点数 C.小于5的点数 D.大于5的点数
2.八(3)班七个兴趣小组人数分别为4、4、5、、6、6、7,已知这组数据的平均数是5,则这组数据的中位数是( )
A.6 B.5 C.4 D.3
3.某班有50人,一次数学测试后,老师对测试成绩进行了统计.由于小颖没有参加此次集体测试,因此计算其他49人的平均分为92分,方差s2=23.后来小颖进行了补测,成绩是92分,关于该班50人的数学测试成绩,下列说法正确的是( )
A.平均分不变,方差变小 B.平均分不变,方差变大
C.平均分和方差都不变 D.平均分和方差都改变
4.已知、是一元二次方程的两个实数根,则的值为( )
A.4 B.-4 C. D.2
5.用配方法解一元二次方程,配方后的方程为( )
A. B. C. D.
6.如图,正五边形ABCDE内接于⊙O,连接AC,则∠ACD的度数是( )
A.72° B.70° C.60° D.45°
7.如图,△ABC中,AB=2,将△ABC绕点A逆时针旋转60°得到△AB1C1,AB1恰好经过点C.则阴影部分的面积为( )
A. B. C. D.
8.如图,为的直径,点C为上的一点,过点C作的切线,交直径的延长线于点D;若,则的度数是( )
A.23° B.44° C.46° D.57°
二、填空题
9.如图,线段AB被等分成5段,在图上任取一点,这一点取在粗线段上的概率是 .
10.“服务社会,提升自我.”凉山州某学校积极开展志愿者服务活动,来自九年级的5名同学(三男两女)成立了“交通秩序维护”小分队.若从该小分队任选两名同学进行交通秩序维护,则恰是一男一女的概率是 .
11.若关于x的方程是一元二次方程,则m的取值范围是 .
12.⊙的半径为,弦,且,,则与的距离为 .
13.一名学生军训时射靶10次,命中的环数分别为4,7,8,6,8,6,5,9,10,7.则这名学生射击环数的方差是 .
14.我国南宋数学家杨辉在1275年提出的一个问题:“直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步?若设阔(宽)为x步,则可列方程 .
15.如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线.
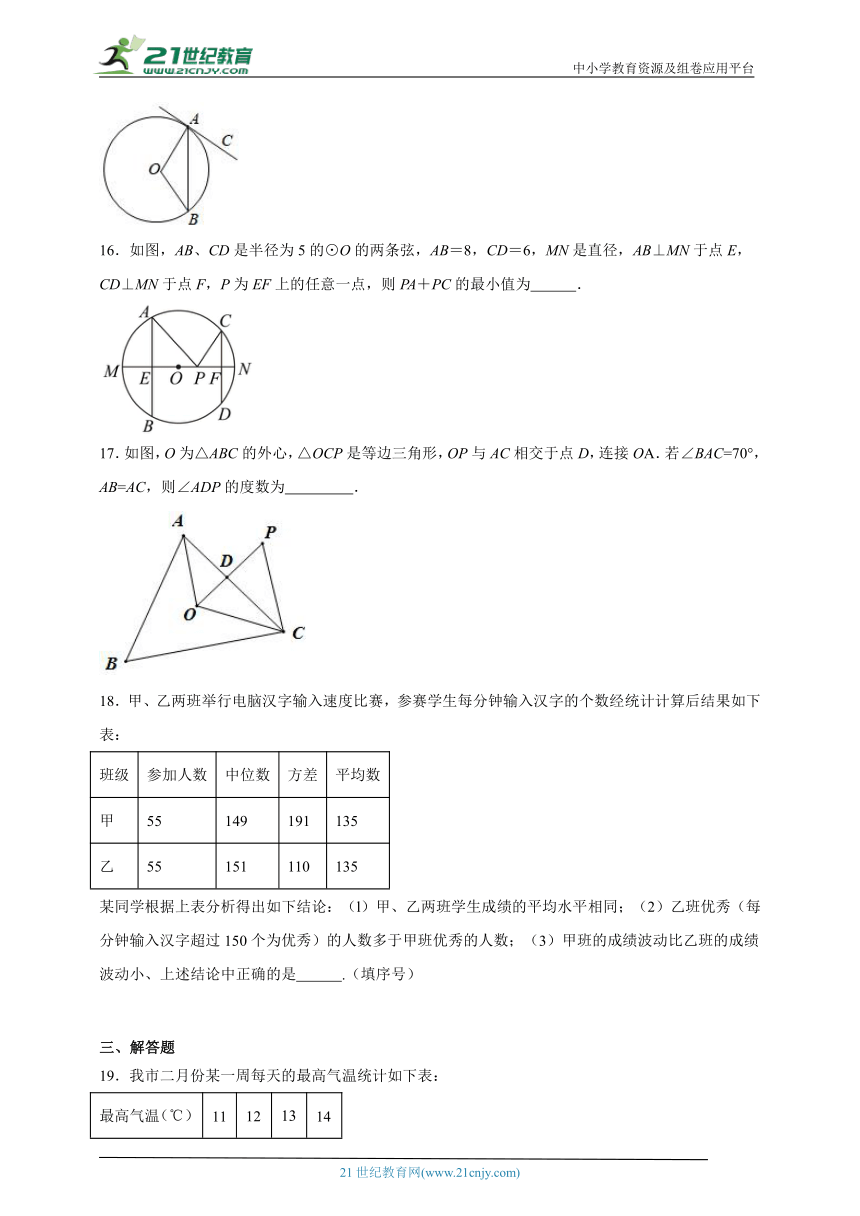
16.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
17.如图,O为△ABC的外心,△OCP是等边三角形,OP与AC相交于点D,连接OA.若∠BAC=70°,AB=AC,则∠ADP的度数为 .
18.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据上表分析得出如下结论:(l)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀(每分钟输入汉字超过150个为优秀)的人数多于甲班优秀的人数;(3)甲班的成绩波动比乙班的成绩波动小、上述结论中正确的是 .(填序号)
三、解答题
19.我市二月份某一周每天的最高气温统计如下表:
最高气温
天数(天)
(1)求这一周最高气温这组数据的众数与中位数;
(2)求这一周最高气温这组数据的极差与方差.
20.已知:关于x的方程
(1)请说明:方程总有两个不相等的实数根;
(2)若方程有一个根为3,求m的值.
21.一起感悟读书之美,推广全民阅读,建设“书香中国”,犹如点亮一座灯塔,撒播一抔种子、开凿一眼清泉.如今,全民阅读已蔚然成风,氤氲书香正飘满中国,听总书记分享他的读书故事,一起感语读书之美,不负韶华梦,读书正当时!某校对A.《三国演义》、B.《红楼梦》、C.《西游记》、D.《水浒传》四大名著开展“传统文化经典著作”推荐阅读活动.
(1)小云从这4部名著中,随机选择1部阅读,他选中《红楼梦》的概率为 .
(2)该校拟从这4部名著中,选择2部作为课外阅读书籍.求《红楼梦》被选中的概率.
22.某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售_______________件,每件盈利____________元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
23.在圆柱形油槽内装入一些油以后,截面如图.截面圆的直径为200cm,若油面的宽AB=160cm,求油槽中油的最大深度.
24.如图,是直径,是的弦,,求的度数.
25.如图,内接于,且为的直径,过点作的切线交的延长线于点,点在直径上,且,连接并延长交于点.连接,,试判断与的数量关系,并说明理由.
参考答案:
1.C
【分析】根据概率公式,分别求出各个选项的概率即可.
【详解】解:A、;
B、;
C、;
D、;
∵,
∴骰子停止后,出现可能性大的是小于5的点数,
故选:C.
【点睛】本题考查了等可能事件的概率,解题的关键是熟知概率计算的公式.
2.B
【分析】本题可先算出x的值,再把数据按从小到大的顺序排列,找出最中间的数,即为中位数.
【详解】解:∵某班七个兴趣小组人数分别为4,4,5,x,6,6,7.已知这组数据的平均数是5,
∴x=5×7 4 4 5 6 6 7=3,
∴这一组数从小到大排列为:3,4,4,5,6,6,7,
∴这组数据的中位数是:5.
故选:B.
【点睛】本题考查的是中位数和平均数的定义,熟知中位数的定义是解答此题的关键.
3.A
【分析】根据平均数,方差的定义计算即可.
【详解】解:∵小颖的成绩和其他49人的平均数相同,都是92分,
∴该班50人的测试成绩的平均分为92分,方差变小,
故选:A.
【点睛】本题考查了方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
4.A
【分析】根据根与系数的关系得,,利用代数式变形得到,然后利用整体代入的方法计算.
【详解】解:根据题意得,,则
.
故选:A.
【点睛】本题考查了一元二次方程根与系数的关系:若是一元二次方程的两根,,.
5.A
【分析】两边配上一次项系数一半的平方,写成完全平方式即可得到答案.
【详解】∵,
∴,
则,
即,
故选:A.
【点睛】此题考查配方法解一元二次方程,掌握配方法是解题的关键.
6.A
【分析】由正五边形的性质可知△ABC是等腰三角形,求出∠B,的度数即可解决问题.
【详解】解:在正五边形ABCDE中,
∠B=∠BCD=×(5-2)×180=108°,AB=BC,
∴∠BCA=∠BAC=(180°-108°)=36°,
∴∠ACD=∠BCD-∠ACB=108°-36°=72°.
故选:A.
【点睛】本题主要考查了正多边形与圆,多边形内角与外角的知识点,解答本题的关键是求出正五边形的内角,此题基础题,比较简单.
7.A
【分析】根据旋转的性质可知,由此可得,根据扇形面积公式即可得出结论.
【详解】由旋转得:∠B1AB=60°,
∵,
∴==.
故选:A.
【点睛】本题主要考查了旋转的性质以及扇形的面积公式,解决本题的的关键根据旋转的性质找出阴影部分的面积等于扇形的面积.
8.B
【分析】连接,由切线的性质可得由圆周角定理可求得的度数,再由直角三角形两锐角互余即可求得答案.
【详解】解:连接,如图,
为的切线,
,
,
,
.
故选:B.
【点睛】本题考查了切线的性质,圆周角定理等,正确添加辅助线,熟练运用相关知识是解题的关键.
9.
【分析】先求出粗线段的长,然后根据概率公式即可得出答案.
【详解】∵线段AB被等分成5段,粗线段有2段,
∴在图上任取一点,这一点取在粗线段上的概率为.
故答案为.
【点睛】本题考查了概率公式,关键是求出粗线段的长,用到的知识点为:概率=粗线段长与总线段长之比.
10.
【详解】根据题意画出树状图如下:
∵一共有20种情况,恰好是一男一女的有12种情况,
∴P(恰好是一男一女)=.
11./
【分析】根据一元二次方程存在的条件,求解即可.
【详解】解:∵关于x的方程是一元二次方程,
∴m-3≠0,
即m≠3,
故答案为:m≠3.
【点睛】本题考查了一元二次方程的概念,一元二次方程需满足:整式方程、化简后只含一个未知数且未知数最高次数为2、二次项系数不为0.
12.7cm或1cm/1cm或7cm
【分析】分当两条弦位于圆心O的同侧和异侧两种情况,分别利用垂径定理和勾股定理解答即可.
【详解】解:当两条弦位于圆心O同侧时,
如图1:过O作OE⊥AB,交AB于点E,交CD于点F,连接OA,OC,
∵AB∥CD,
∴OE⊥CD,
∴E、F分别为AB、CD的中点,
∴AE=BE=AB=4m,CF=DF=CD=3m,
在Rt△COF中,OC=5cm,C34cm,
根据勾股定理得:OF=4m,
在Rt△AOE中,OA=5cm,AE=4m,
根据勾股定理得:OE═3m,
则EF=OF-OE=4-3=1cm;
当两条弦位于圆心O异侧时,
如图2:过O作OE⊥AB,交AB于点E,交CD于点F,连接OA,OC,
∵AB∥CD,
∴OE⊥CD,
∴E、F分别为AB、CD的中点,
∴AE=BE=AB=4m,CF=DF=CD=3m,
在Rt△COF中,OC=5cm,CF=3cm,
根据勾股定理得:OF=4m,
在Rt△AOE中,OA=5cm,AE=4m,
根据勾股定理得:OE═3m,
则EF=OF+OE=4+3=7cm.
故填:7cm或1cm.
【点睛】本题主要考查了勾股定理和垂径定理,掌握分类讨论思想成为解答本题的关键.
13.3.
【分析】先计算出平均数,再根据方差公式列式计算即可.
【详解】解:∵这组数据的平均数是(4+7+8+6+8+6+5+9+10+7)÷10=7,
∴这名学生射击环数的方差
= [(4-7)2+(7-7)2+(8-7)2+(6-7)2+(8-7)2+(6-7)2+(5-7)2+(9-7)2+(10-7)2+(7-7)2]
= (9+0+1+1+1+1+4+4+9+0)
=3.
故答案为3.
【点睛】本题考查方差:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1-)2+(x2-)2+…+(xn-)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
14.x(x+12)=864
【分析】利用长乘以宽=864,列出方程即可得出答案.
【详解】解:设阔(宽)为x步,则所列方程为:x(x+12)=864.
故答案为:x(x+12)=864.
【点睛】此题主要考查了由实际问题抽象出一元二次方程,正确表示出矩形的长是解题关键.
15.60
【分析】由已知可求得∠OAB的度数,因为OA⊥AC,AC才能成为⊙O的切线,从而可求得∠CAB的度数.
【详解】解:∵△AOB中,OA=OB,∠AOB=120°,
∴,
∵当OA⊥AC即∠OAC=90°时,AC才能成为⊙O的切线,
∴当∠CAB的度数等于60°,即OA⊥AC时,AC才能成为⊙O的切线.
故答案为:60.
【点睛】本题考查了切线的判定,三角形内角和定理,等腰三角形的性质,掌握切线的判定定理是解答此题的关键.
16.7
【分析】连接OA、OB、OC,作CH⊥AB,用勾股定理算得EF=OE+OF=7,CH=7,在直角三角形CHB中求出BC即可得到答案.
【详解】解:如图,
连接OA、OB、OC,作CH⊥AB于H.
根据垂径定理,得到BE=AB=4,CF=CD=3,
∴OE===3,OF=,
∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为7.
故答案为:7.
【点睛】此题考查了圆的垂径定理,圆中最短路径问题以及勾股定理,熟练掌握垂径定理及勾股定理是解题的关键.
17.85°/85度
【分析】根据题意利用三角形外心的性质以及利用等腰三角形的性质得出∠OAC=∠OCA=35°,进而结合三角形外角的性质得出答案.
【详解】解:∵O为△ABC的外心,∠BAC=70°,AB=AC,
∴∠OAC=35°,AO=CO,
∴∠OAC=∠OCA=35°,
∴∠AOC=110°,
∵△OCP为正三角形,
∴∠COP =60°,
∴∠AOP=∠AOC -∠COP =50°,
∴∠ADP=∠OAD+∠AOD=85°.
故选:85°.
【点睛】本题主要考查三角形的外心的性质以及等边三角形的性质等知识,得出∠OAC=∠OCA=35°是解题的关键.
18.(1),(2).
【分析】平均水平的判断主要分析平均数;优秀人数的判断从中位数不同可以得到;波动大小比较方差的大小.
【详解】解:从表中可知,平均字数都是135,(1)正确;
甲班的中位数是149,乙班的中位数是151,比甲的多,而平均数都要为135,说明乙的优秀人数多于甲班的,(2)正确;
甲班的方差大于乙班的,则说明乙班的波动小,所以(3)错误.
(1)(2)正确.
故答案为(1)(2).
【点睛】本题考查了平均数,中位数,方差的意义.平均数平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
19.(1)众数为11,中位数为12
(2)极差为3,方差为
【分析】(1)根据将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,以及一组数据中出现次数最多的数据叫做众数.分别求出即可;
(2)根据极差是指一组数据中最大数据与最小数据的差,极差最大值最小值,以及方差公式求出即可.
【详解】(1)解:根据图表得出数据有:11,11,11,12,12,13,14,
根据众数定义出现次数最多的是众数,
这组数据的众数为:11,
中位数为第4个数:12;
(2)根据极差最大值最小值,
极差为:,
这组数据的平均数为:,
方差为:
.
【点睛】此题考查了确定一组数据的中位数和众数以及极差与方差等知识,一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
20.(1)见解析
(2)
【分析】(1)计算一元二次方程根的判别式,根据判别式即可得出结论;
(2)将代入原方程,得到关于的一元二次方程,解方程即可求解.
【详解】(1)解:∵中,,
∴原方程总有两个不相等的实数根;
(2)解:∵方程有一个根为3,令代入原方程,得
,
即,
,
∴,
【点睛】本题考查了一元二次方程根的判别式,一元二次方程的解,因式分解法解一元二次方程,正确的计算是解题的关键.
21.(1)
(2)
【分析】(1)直接利用概率公式求解即可.
(2)画树状图得出所有等可能的结果数和《红楼梦》被选中的结果数,再利用概率公式可得出答案.
【详解】(1)解:∵共有4部名著,
∴随机选择1部为《红楼梦》的概率为.
(2)画树状图如下:
共有12种等可能的结果,其中《红楼梦》被选中的结果有6种,
∴《红楼梦》被选中的概率为.
【点睛】本题考查列表法与树状图法,熟练掌握概率公式是解答本题的关键.用到的知识点为:概率=所求情况数与总情况数之比.
22.(1);
(2)每件童装降价20元时,平均每天赢利1200元
(3)不可能平均每天赢利2000元,理由见解析
【分析】(1)根据销售量=原销售量+因价格下降增加的销售量,每件的利润=实际售价-进价,列式即可;
(2)根据总利润=每件的利润×销售数量,列方程求解即可;
(3)根据总利润=每件的利润×销售数量,列方程求解即可.
【详解】(1)解:设每件童装降价x元时,每天可销售件,每件盈利元,
故答案为:,;
(2)依题可得:,
∴,
∴,
∴,,
扩大销售量,增加利润,
,
答:每件童装降价20元时,平均每天赢利1200元;
(3)根据题意得:,
∴,
∴△= =-4×1×600=-15000,
∴原方程无解.
答:不可能平均每天赢利2000元.
【点睛】本题考查了一元二次方程的实际应用,理解题意找出题目蕴含的等量关系是解本题的关键.
23.油槽中油的最大深度为
【分析】过作于 交于 则 由 结合勾股定理求解 从而可得答案.
【详解】解:过作于 交于
则
截面圆的直径为200cm,油面的宽AB=160cm,
所以油槽中油的最大深度为
【点睛】本题考查的是垂径定理的实际应用,掌握利用垂径定理解决油槽深度问题是解题的关键.
24.
【分析】连接BC,利用直径对的圆周角是 ,得到,再利用同弧所对的圆周角相等,得到,最后利用三角形内角和定理即可求解.
【详解】解:连接.
是的直径
.
=
即
【点睛】本题考查了直径所对的圆周角是直角,已经同弧所对的圆周角相等的基本知识,属于基础题.
25.AF=BF,理由见解析.
【分析】连接,,可得,再根据,可得,然后得出,可得出OF是AB垂直平分线即可得出结论.
【详解】解:.理由如下:
如图,连接,.
是的切线,
,
,
,
,
,
,
,
,
又,
,
,
,
,
∴OF垂直平分AB
.
【点睛】本题考查了圆的切线相关性质,等腰三角形的性质,垂直平分线等,解题的关键是认清图形,抽象出各几何图形的特殊位置关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末经典题型练习(二)2023-2024学年九年级上册苏科版
一、单选题
1.掷一枚质地均匀的骰子,骰子停止后,出现可能性大的是( )
A.小于3的点数 B.大于3的点数 C.小于5的点数 D.大于5的点数
2.八(3)班七个兴趣小组人数分别为4、4、5、、6、6、7,已知这组数据的平均数是5,则这组数据的中位数是( )
A.6 B.5 C.4 D.3
3.某班有50人,一次数学测试后,老师对测试成绩进行了统计.由于小颖没有参加此次集体测试,因此计算其他49人的平均分为92分,方差s2=23.后来小颖进行了补测,成绩是92分,关于该班50人的数学测试成绩,下列说法正确的是( )
A.平均分不变,方差变小 B.平均分不变,方差变大
C.平均分和方差都不变 D.平均分和方差都改变
4.已知、是一元二次方程的两个实数根,则的值为( )
A.4 B.-4 C. D.2
5.用配方法解一元二次方程,配方后的方程为( )
A. B. C. D.
6.如图,正五边形ABCDE内接于⊙O,连接AC,则∠ACD的度数是( )
A.72° B.70° C.60° D.45°
7.如图,△ABC中,AB=2,将△ABC绕点A逆时针旋转60°得到△AB1C1,AB1恰好经过点C.则阴影部分的面积为( )
A. B. C. D.
8.如图,为的直径,点C为上的一点,过点C作的切线,交直径的延长线于点D;若,则的度数是( )
A.23° B.44° C.46° D.57°
二、填空题
9.如图,线段AB被等分成5段,在图上任取一点,这一点取在粗线段上的概率是 .
10.“服务社会,提升自我.”凉山州某学校积极开展志愿者服务活动,来自九年级的5名同学(三男两女)成立了“交通秩序维护”小分队.若从该小分队任选两名同学进行交通秩序维护,则恰是一男一女的概率是 .
11.若关于x的方程是一元二次方程,则m的取值范围是 .
12.⊙的半径为,弦,且,,则与的距离为 .
13.一名学生军训时射靶10次,命中的环数分别为4,7,8,6,8,6,5,9,10,7.则这名学生射击环数的方差是 .
14.我国南宋数学家杨辉在1275年提出的一个问题:“直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步?若设阔(宽)为x步,则可列方程 .
15.如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线.
16.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
17.如图,O为△ABC的外心,△OCP是等边三角形,OP与AC相交于点D,连接OA.若∠BAC=70°,AB=AC,则∠ADP的度数为 .
18.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据上表分析得出如下结论:(l)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀(每分钟输入汉字超过150个为优秀)的人数多于甲班优秀的人数;(3)甲班的成绩波动比乙班的成绩波动小、上述结论中正确的是 .(填序号)
三、解答题
19.我市二月份某一周每天的最高气温统计如下表:
最高气温
天数(天)
(1)求这一周最高气温这组数据的众数与中位数;
(2)求这一周最高气温这组数据的极差与方差.
20.已知:关于x的方程
(1)请说明:方程总有两个不相等的实数根;
(2)若方程有一个根为3,求m的值.
21.一起感悟读书之美,推广全民阅读,建设“书香中国”,犹如点亮一座灯塔,撒播一抔种子、开凿一眼清泉.如今,全民阅读已蔚然成风,氤氲书香正飘满中国,听总书记分享他的读书故事,一起感语读书之美,不负韶华梦,读书正当时!某校对A.《三国演义》、B.《红楼梦》、C.《西游记》、D.《水浒传》四大名著开展“传统文化经典著作”推荐阅读活动.
(1)小云从这4部名著中,随机选择1部阅读,他选中《红楼梦》的概率为 .
(2)该校拟从这4部名著中,选择2部作为课外阅读书籍.求《红楼梦》被选中的概率.
22.某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售_______________件,每件盈利____________元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
23.在圆柱形油槽内装入一些油以后,截面如图.截面圆的直径为200cm,若油面的宽AB=160cm,求油槽中油的最大深度.
24.如图,是直径,是的弦,,求的度数.
25.如图,内接于,且为的直径,过点作的切线交的延长线于点,点在直径上,且,连接并延长交于点.连接,,试判断与的数量关系,并说明理由.
参考答案:
1.C
【分析】根据概率公式,分别求出各个选项的概率即可.
【详解】解:A、;
B、;
C、;
D、;
∵,
∴骰子停止后,出现可能性大的是小于5的点数,
故选:C.
【点睛】本题考查了等可能事件的概率,解题的关键是熟知概率计算的公式.
2.B
【分析】本题可先算出x的值,再把数据按从小到大的顺序排列,找出最中间的数,即为中位数.
【详解】解:∵某班七个兴趣小组人数分别为4,4,5,x,6,6,7.已知这组数据的平均数是5,
∴x=5×7 4 4 5 6 6 7=3,
∴这一组数从小到大排列为:3,4,4,5,6,6,7,
∴这组数据的中位数是:5.
故选:B.
【点睛】本题考查的是中位数和平均数的定义,熟知中位数的定义是解答此题的关键.
3.A
【分析】根据平均数,方差的定义计算即可.
【详解】解:∵小颖的成绩和其他49人的平均数相同,都是92分,
∴该班50人的测试成绩的平均分为92分,方差变小,
故选:A.
【点睛】本题考查了方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
4.A
【分析】根据根与系数的关系得,,利用代数式变形得到,然后利用整体代入的方法计算.
【详解】解:根据题意得,,则
.
故选:A.
【点睛】本题考查了一元二次方程根与系数的关系:若是一元二次方程的两根,,.
5.A
【分析】两边配上一次项系数一半的平方,写成完全平方式即可得到答案.
【详解】∵,
∴,
则,
即,
故选:A.
【点睛】此题考查配方法解一元二次方程,掌握配方法是解题的关键.
6.A
【分析】由正五边形的性质可知△ABC是等腰三角形,求出∠B,的度数即可解决问题.
【详解】解:在正五边形ABCDE中,
∠B=∠BCD=×(5-2)×180=108°,AB=BC,
∴∠BCA=∠BAC=(180°-108°)=36°,
∴∠ACD=∠BCD-∠ACB=108°-36°=72°.
故选:A.
【点睛】本题主要考查了正多边形与圆,多边形内角与外角的知识点,解答本题的关键是求出正五边形的内角,此题基础题,比较简单.
7.A
【分析】根据旋转的性质可知,由此可得,根据扇形面积公式即可得出结论.
【详解】由旋转得:∠B1AB=60°,
∵,
∴==.
故选:A.
【点睛】本题主要考查了旋转的性质以及扇形的面积公式,解决本题的的关键根据旋转的性质找出阴影部分的面积等于扇形的面积.
8.B
【分析】连接,由切线的性质可得由圆周角定理可求得的度数,再由直角三角形两锐角互余即可求得答案.
【详解】解:连接,如图,
为的切线,
,
,
,
.
故选:B.
【点睛】本题考查了切线的性质,圆周角定理等,正确添加辅助线,熟练运用相关知识是解题的关键.
9.
【分析】先求出粗线段的长,然后根据概率公式即可得出答案.
【详解】∵线段AB被等分成5段,粗线段有2段,
∴在图上任取一点,这一点取在粗线段上的概率为.
故答案为.
【点睛】本题考查了概率公式,关键是求出粗线段的长,用到的知识点为:概率=粗线段长与总线段长之比.
10.
【详解】根据题意画出树状图如下:
∵一共有20种情况,恰好是一男一女的有12种情况,
∴P(恰好是一男一女)=.
11./
【分析】根据一元二次方程存在的条件,求解即可.
【详解】解:∵关于x的方程是一元二次方程,
∴m-3≠0,
即m≠3,
故答案为:m≠3.
【点睛】本题考查了一元二次方程的概念,一元二次方程需满足:整式方程、化简后只含一个未知数且未知数最高次数为2、二次项系数不为0.
12.7cm或1cm/1cm或7cm
【分析】分当两条弦位于圆心O的同侧和异侧两种情况,分别利用垂径定理和勾股定理解答即可.
【详解】解:当两条弦位于圆心O同侧时,
如图1:过O作OE⊥AB,交AB于点E,交CD于点F,连接OA,OC,
∵AB∥CD,
∴OE⊥CD,
∴E、F分别为AB、CD的中点,
∴AE=BE=AB=4m,CF=DF=CD=3m,
在Rt△COF中,OC=5cm,C34cm,
根据勾股定理得:OF=4m,
在Rt△AOE中,OA=5cm,AE=4m,
根据勾股定理得:OE═3m,
则EF=OF-OE=4-3=1cm;
当两条弦位于圆心O异侧时,
如图2:过O作OE⊥AB,交AB于点E,交CD于点F,连接OA,OC,
∵AB∥CD,
∴OE⊥CD,
∴E、F分别为AB、CD的中点,
∴AE=BE=AB=4m,CF=DF=CD=3m,
在Rt△COF中,OC=5cm,CF=3cm,
根据勾股定理得:OF=4m,
在Rt△AOE中,OA=5cm,AE=4m,
根据勾股定理得:OE═3m,
则EF=OF+OE=4+3=7cm.
故填:7cm或1cm.
【点睛】本题主要考查了勾股定理和垂径定理,掌握分类讨论思想成为解答本题的关键.
13.3.
【分析】先计算出平均数,再根据方差公式列式计算即可.
【详解】解:∵这组数据的平均数是(4+7+8+6+8+6+5+9+10+7)÷10=7,
∴这名学生射击环数的方差
= [(4-7)2+(7-7)2+(8-7)2+(6-7)2+(8-7)2+(6-7)2+(5-7)2+(9-7)2+(10-7)2+(7-7)2]
= (9+0+1+1+1+1+4+4+9+0)
=3.
故答案为3.
【点睛】本题考查方差:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1-)2+(x2-)2+…+(xn-)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
14.x(x+12)=864
【分析】利用长乘以宽=864,列出方程即可得出答案.
【详解】解:设阔(宽)为x步,则所列方程为:x(x+12)=864.
故答案为:x(x+12)=864.
【点睛】此题主要考查了由实际问题抽象出一元二次方程,正确表示出矩形的长是解题关键.
15.60
【分析】由已知可求得∠OAB的度数,因为OA⊥AC,AC才能成为⊙O的切线,从而可求得∠CAB的度数.
【详解】解:∵△AOB中,OA=OB,∠AOB=120°,
∴,
∵当OA⊥AC即∠OAC=90°时,AC才能成为⊙O的切线,
∴当∠CAB的度数等于60°,即OA⊥AC时,AC才能成为⊙O的切线.
故答案为:60.
【点睛】本题考查了切线的判定,三角形内角和定理,等腰三角形的性质,掌握切线的判定定理是解答此题的关键.
16.7
【分析】连接OA、OB、OC,作CH⊥AB,用勾股定理算得EF=OE+OF=7,CH=7,在直角三角形CHB中求出BC即可得到答案.
【详解】解:如图,
连接OA、OB、OC,作CH⊥AB于H.
根据垂径定理,得到BE=AB=4,CF=CD=3,
∴OE===3,OF=,
∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为7.
故答案为:7.
【点睛】此题考查了圆的垂径定理,圆中最短路径问题以及勾股定理,熟练掌握垂径定理及勾股定理是解题的关键.
17.85°/85度
【分析】根据题意利用三角形外心的性质以及利用等腰三角形的性质得出∠OAC=∠OCA=35°,进而结合三角形外角的性质得出答案.
【详解】解:∵O为△ABC的外心,∠BAC=70°,AB=AC,
∴∠OAC=35°,AO=CO,
∴∠OAC=∠OCA=35°,
∴∠AOC=110°,
∵△OCP为正三角形,
∴∠COP =60°,
∴∠AOP=∠AOC -∠COP =50°,
∴∠ADP=∠OAD+∠AOD=85°.
故选:85°.
【点睛】本题主要考查三角形的外心的性质以及等边三角形的性质等知识,得出∠OAC=∠OCA=35°是解题的关键.
18.(1),(2).
【分析】平均水平的判断主要分析平均数;优秀人数的判断从中位数不同可以得到;波动大小比较方差的大小.
【详解】解:从表中可知,平均字数都是135,(1)正确;
甲班的中位数是149,乙班的中位数是151,比甲的多,而平均数都要为135,说明乙的优秀人数多于甲班的,(2)正确;
甲班的方差大于乙班的,则说明乙班的波动小,所以(3)错误.
(1)(2)正确.
故答案为(1)(2).
【点睛】本题考查了平均数,中位数,方差的意义.平均数平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
19.(1)众数为11,中位数为12
(2)极差为3,方差为
【分析】(1)根据将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,以及一组数据中出现次数最多的数据叫做众数.分别求出即可;
(2)根据极差是指一组数据中最大数据与最小数据的差,极差最大值最小值,以及方差公式求出即可.
【详解】(1)解:根据图表得出数据有:11,11,11,12,12,13,14,
根据众数定义出现次数最多的是众数,
这组数据的众数为:11,
中位数为第4个数:12;
(2)根据极差最大值最小值,
极差为:,
这组数据的平均数为:,
方差为:
.
【点睛】此题考查了确定一组数据的中位数和众数以及极差与方差等知识,一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
20.(1)见解析
(2)
【分析】(1)计算一元二次方程根的判别式,根据判别式即可得出结论;
(2)将代入原方程,得到关于的一元二次方程,解方程即可求解.
【详解】(1)解:∵中,,
∴原方程总有两个不相等的实数根;
(2)解:∵方程有一个根为3,令代入原方程,得
,
即,
,
∴,
【点睛】本题考查了一元二次方程根的判别式,一元二次方程的解,因式分解法解一元二次方程,正确的计算是解题的关键.
21.(1)
(2)
【分析】(1)直接利用概率公式求解即可.
(2)画树状图得出所有等可能的结果数和《红楼梦》被选中的结果数,再利用概率公式可得出答案.
【详解】(1)解:∵共有4部名著,
∴随机选择1部为《红楼梦》的概率为.
(2)画树状图如下:
共有12种等可能的结果,其中《红楼梦》被选中的结果有6种,
∴《红楼梦》被选中的概率为.
【点睛】本题考查列表法与树状图法,熟练掌握概率公式是解答本题的关键.用到的知识点为:概率=所求情况数与总情况数之比.
22.(1);
(2)每件童装降价20元时,平均每天赢利1200元
(3)不可能平均每天赢利2000元,理由见解析
【分析】(1)根据销售量=原销售量+因价格下降增加的销售量,每件的利润=实际售价-进价,列式即可;
(2)根据总利润=每件的利润×销售数量,列方程求解即可;
(3)根据总利润=每件的利润×销售数量,列方程求解即可.
【详解】(1)解:设每件童装降价x元时,每天可销售件,每件盈利元,
故答案为:,;
(2)依题可得:,
∴,
∴,
∴,,
扩大销售量,增加利润,
,
答:每件童装降价20元时,平均每天赢利1200元;
(3)根据题意得:,
∴,
∴△= =-4×1×600=-15000,
∴原方程无解.
答:不可能平均每天赢利2000元.
【点睛】本题考查了一元二次方程的实际应用,理解题意找出题目蕴含的等量关系是解本题的关键.
23.油槽中油的最大深度为
【分析】过作于 交于 则 由 结合勾股定理求解 从而可得答案.
【详解】解:过作于 交于
则
截面圆的直径为200cm,油面的宽AB=160cm,
所以油槽中油的最大深度为
【点睛】本题考查的是垂径定理的实际应用,掌握利用垂径定理解决油槽深度问题是解题的关键.
24.
【分析】连接BC,利用直径对的圆周角是 ,得到,再利用同弧所对的圆周角相等,得到,最后利用三角形内角和定理即可求解.
【详解】解:连接.
是的直径
.
=
即
【点睛】本题考查了直径所对的圆周角是直角,已经同弧所对的圆周角相等的基本知识,属于基础题.
25.AF=BF,理由见解析.
【分析】连接,,可得,再根据,可得,然后得出,可得出OF是AB垂直平分线即可得出结论.
【详解】解:.理由如下:
如图,连接,.
是的切线,
,
,
,
,
,
,
,
,
又,
,
,
,
,
∴OF垂直平分AB
.
【点睛】本题考查了圆的切线相关性质,等腰三角形的性质,垂直平分线等,解题的关键是认清图形,抽象出各几何图形的特殊位置关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
