【核心素养目标】苏科版八年级数学上册1.3 第5课时 利用“ASA”与“AAS”判定三角形全等 课件(共24张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版八年级数学上册1.3 第5课时 利用“ASA”与“AAS”判定三角形全等 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 19:32:55 | ||
图片预览








文档简介
(共24张PPT)
第1章 全等三角形
1.3 探索三角形全等的条件
第5课时 利用“ASA”与“AAS”判定三角形全等
1.能根据题意恰当选用“ASA”或“AAS”判定两个三角形全等.
2.能熟练运用“ASA”和“AAS”解决生活中的实际问题,发展学生的抽象思维、逻辑推理与论证表达能力.
◎重点:能根据题意恰当选用“ASA”或“AAS”判定两个三角形全等.
◎难点:能熟练运用“ASA”和“AAS”解决生活中的实际问题.
1.能够 完全重合 的两个三角形叫做全等三角形.
2.目前学过的判定两个三角形全等的方法有哪些?
边角边: 两边 及其 夹角 分别相等的两个三角形全等.
角边角:有 两角及夹边 分别相等的两个三角形全等.
角角边:有 两角 分别相等且其中一组等角的 对边 相等的两个三角形全等.
完全重合
两边
夹角
两角及夹边
两角
对边
·导学建议·
回顾之前学过的判定定理,唤醒旧知,为本课时学习如何选择恰当的判定方法作铺垫.(准备直尺、白纸)
利用“ASA”与“AAS”判定三角形全等
阅读课本本课时相关内容,回答下列问题.
思考 (1)如图1,∠A=∠B,∠l=∠2,EA=EB.你能证明AC=BD吗?
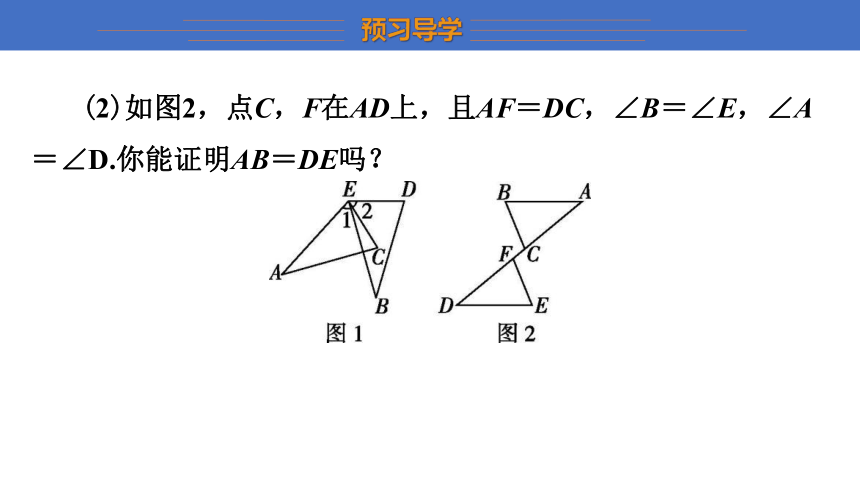
(2)如图2,点C,F在AD上,且AF=DC,∠B=∠E,∠A=∠D.你能证明AB=DE吗?
答:(1)证明:∵∠1=∠2,在△AEC和△BED中,∴△AEC≌△BED(ASA),∴AC=BD.
(2)证明:∵AF=DC,∴AF-CF=DC-CF,即AC=DF,在△ABC和△DEF中,
∴△ABC≌△DEF(AAS),∴AB=DE.
·导学建议·
证明三角形全等时,如果题目中给出了两组对应角(或对应边)之间的关系,往往需要通过等式的性质进行二次构造等量关系,解答过程中选用哪个判定定理,则要看“对应边”与“对应角”的位置符合哪个定理规定的位置关系.
归纳总结 用“角边角”定理时,要满足两个三角形 两角及其夹边 对应相等的条件.
用“角角边”定理时,要满足两个三角形 两角 分别相等且其中的一组等角的 对边 相等的条件.
两角
及其夹边
两角
对边
·导学建议·
在例6中,由于结论中的线段AB,CD不是图中哪个三角形的边,所以分析的要求较高.此外在本例的教学中,应把重点放在引导学生充分的讨论、交流上.在实际教学中,部分学生经历前面的情境活动和探索活动,能够有条理的思考和表达解答本例的思路,对于有困难的学生,教师应给予适当的帮助,引导他们用图形的运动来识图,给出示范的分析以及本例的推证过程.课本提供了综合法和用符号“ ”表述的两种表述方式,教学时,可以引导学生把两种表述过程对照起来看,有利于学生理清思路.
如图,已知AC与BD相交于点P,AB∥CD,P为AC的中点,若CD=7,AE=3,求BE的长.
解:∵AB∥CD,∴∠B=∠D,∠A=∠PCD.∵P为AC的中点,∴AP=PC.在△ABP和△CDP中,∴△ABP≌△CDP(AAS),∴AB=CD=7,∴BE=AB-AE=4.
添加合适的条件证明三角形全等
1.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AB=BE,∠ABC=∠E,请添加一个条件,使△ABC≌△BED,并以选择的条件写出证明过程.
①若添加的条件是BC=DE,证明过程如下:
在△ABC和△BED中,
∴△ABC≌△BED(SAS).
解:可以添加BC=DE或∠A=∠EBD或∠ACB=∠D.
②若添加的条件是∠A=∠EBD,证明过程如下:
在△ABC和△BED中,
∴△ABC≌△BED(ASA).
③若添加的条件是∠ACB=∠D,证明过程如下:
在△ABC和△BED中,
∴△ABC≌△BED(AAS).
变式演练 如图,AB=CB.要证明△ABE≌△CBD,如果直接利用“ASA”,那么需要补充的条件是 ∠A=∠C ;如果直接利用“AAS”,那么需要补充的条件是 ∠AEB=∠CDB .
∠A=∠C
∠AEB=
∠CDB
方法归纳交流 开放型试题,答案或解法不唯一,具体分析要判定全等的两个三角形已具备的条件,再根据可能使用的判定方法对应找出所缺少的条件(不同的判定方法往往对应不同的添加条件,此外有一组边相等是判定三角形全等必不可少的条件).
添加辅助线构造三角形全等解决面积问题
2.如图,∠ABC=∠ACD=90°,BC=2,AC=CD,求△BCD的面积.
解:如图,过点D作DH⊥BC,交BC的延长线于点H.
∵∠ABC=90°,∴∠BAC+∠ACB=90°.∵∠ACD=90°,∴∠HCD+∠ACB=90°,∴∠BAC=∠HCD,在△ABC和△CHD中,∴△ABC≌△CHD(AAS),
∴DH=BC=2,
∴△BCD的面积为×BC×DH=×2×2=2.
∴△BCD的面积为×BC×DH=×2×2=2.
变式演练 如图,△ABC的面积为5 cm2,AP垂直∠B的平分线BP于点P,则△PBC的面积为 cm2 .
cm2
方法归纳交流 解题的关键是学会添加常用辅助线,构造全等三角形,再根据全等三角形面积相等、等高模型知识进行求解.
第1章 全等三角形
1.3 探索三角形全等的条件
第5课时 利用“ASA”与“AAS”判定三角形全等
1.能根据题意恰当选用“ASA”或“AAS”判定两个三角形全等.
2.能熟练运用“ASA”和“AAS”解决生活中的实际问题,发展学生的抽象思维、逻辑推理与论证表达能力.
◎重点:能根据题意恰当选用“ASA”或“AAS”判定两个三角形全等.
◎难点:能熟练运用“ASA”和“AAS”解决生活中的实际问题.
1.能够 完全重合 的两个三角形叫做全等三角形.
2.目前学过的判定两个三角形全等的方法有哪些?
边角边: 两边 及其 夹角 分别相等的两个三角形全等.
角边角:有 两角及夹边 分别相等的两个三角形全等.
角角边:有 两角 分别相等且其中一组等角的 对边 相等的两个三角形全等.
完全重合
两边
夹角
两角及夹边
两角
对边
·导学建议·
回顾之前学过的判定定理,唤醒旧知,为本课时学习如何选择恰当的判定方法作铺垫.(准备直尺、白纸)
利用“ASA”与“AAS”判定三角形全等
阅读课本本课时相关内容,回答下列问题.
思考 (1)如图1,∠A=∠B,∠l=∠2,EA=EB.你能证明AC=BD吗?
(2)如图2,点C,F在AD上,且AF=DC,∠B=∠E,∠A=∠D.你能证明AB=DE吗?
答:(1)证明:∵∠1=∠2,在△AEC和△BED中,∴△AEC≌△BED(ASA),∴AC=BD.
(2)证明:∵AF=DC,∴AF-CF=DC-CF,即AC=DF,在△ABC和△DEF中,
∴△ABC≌△DEF(AAS),∴AB=DE.
·导学建议·
证明三角形全等时,如果题目中给出了两组对应角(或对应边)之间的关系,往往需要通过等式的性质进行二次构造等量关系,解答过程中选用哪个判定定理,则要看“对应边”与“对应角”的位置符合哪个定理规定的位置关系.
归纳总结 用“角边角”定理时,要满足两个三角形 两角及其夹边 对应相等的条件.
用“角角边”定理时,要满足两个三角形 两角 分别相等且其中的一组等角的 对边 相等的条件.
两角
及其夹边
两角
对边
·导学建议·
在例6中,由于结论中的线段AB,CD不是图中哪个三角形的边,所以分析的要求较高.此外在本例的教学中,应把重点放在引导学生充分的讨论、交流上.在实际教学中,部分学生经历前面的情境活动和探索活动,能够有条理的思考和表达解答本例的思路,对于有困难的学生,教师应给予适当的帮助,引导他们用图形的运动来识图,给出示范的分析以及本例的推证过程.课本提供了综合法和用符号“ ”表述的两种表述方式,教学时,可以引导学生把两种表述过程对照起来看,有利于学生理清思路.
如图,已知AC与BD相交于点P,AB∥CD,P为AC的中点,若CD=7,AE=3,求BE的长.
解:∵AB∥CD,∴∠B=∠D,∠A=∠PCD.∵P为AC的中点,∴AP=PC.在△ABP和△CDP中,∴△ABP≌△CDP(AAS),∴AB=CD=7,∴BE=AB-AE=4.
添加合适的条件证明三角形全等
1.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AB=BE,∠ABC=∠E,请添加一个条件,使△ABC≌△BED,并以选择的条件写出证明过程.
①若添加的条件是BC=DE,证明过程如下:
在△ABC和△BED中,
∴△ABC≌△BED(SAS).
解:可以添加BC=DE或∠A=∠EBD或∠ACB=∠D.
②若添加的条件是∠A=∠EBD,证明过程如下:
在△ABC和△BED中,
∴△ABC≌△BED(ASA).
③若添加的条件是∠ACB=∠D,证明过程如下:
在△ABC和△BED中,
∴△ABC≌△BED(AAS).
变式演练 如图,AB=CB.要证明△ABE≌△CBD,如果直接利用“ASA”,那么需要补充的条件是 ∠A=∠C ;如果直接利用“AAS”,那么需要补充的条件是 ∠AEB=∠CDB .
∠A=∠C
∠AEB=
∠CDB
方法归纳交流 开放型试题,答案或解法不唯一,具体分析要判定全等的两个三角形已具备的条件,再根据可能使用的判定方法对应找出所缺少的条件(不同的判定方法往往对应不同的添加条件,此外有一组边相等是判定三角形全等必不可少的条件).
添加辅助线构造三角形全等解决面积问题
2.如图,∠ABC=∠ACD=90°,BC=2,AC=CD,求△BCD的面积.
解:如图,过点D作DH⊥BC,交BC的延长线于点H.
∵∠ABC=90°,∴∠BAC+∠ACB=90°.∵∠ACD=90°,∴∠HCD+∠ACB=90°,∴∠BAC=∠HCD,在△ABC和△CHD中,∴△ABC≌△CHD(AAS),
∴DH=BC=2,
∴△BCD的面积为×BC×DH=×2×2=2.
∴△BCD的面积为×BC×DH=×2×2=2.
变式演练 如图,△ABC的面积为5 cm2,AP垂直∠B的平分线BP于点P,则△PBC的面积为 cm2 .
cm2
方法归纳交流 解题的关键是学会添加常用辅助线,构造全等三角形,再根据全等三角形面积相等、等高模型知识进行求解.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
