北师大版数学九年级下册2.4 二次函数的应用 课件 (共28张PPT)
文档属性
| 名称 | 北师大版数学九年级下册2.4 二次函数的应用 课件 (共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 19:37:10 | ||
图片预览






文档简介
(共28张PPT)
4 二次函数的应用
第1课时 最大面积问题
北师版九年级数学下册
第二章 二次函数
新课导入
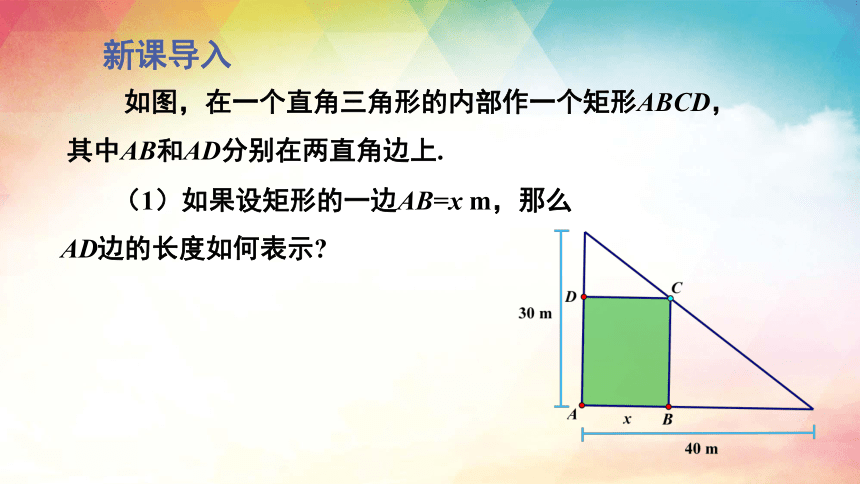
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
(1)如果设矩形的一边AB=x m,那么
AD边的长度如何表示
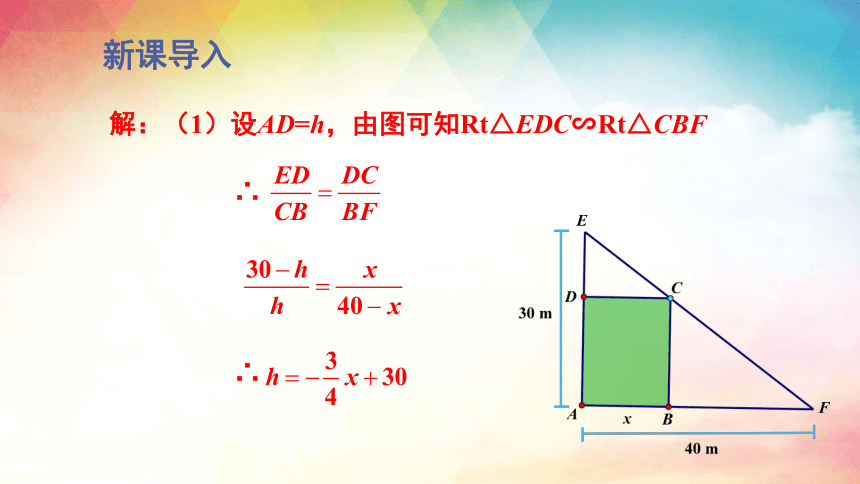
解:(1)设AD=h,由图可知Rt△EDC∽Rt△CBF
∴
∴
新课导入
E
F
新课导入
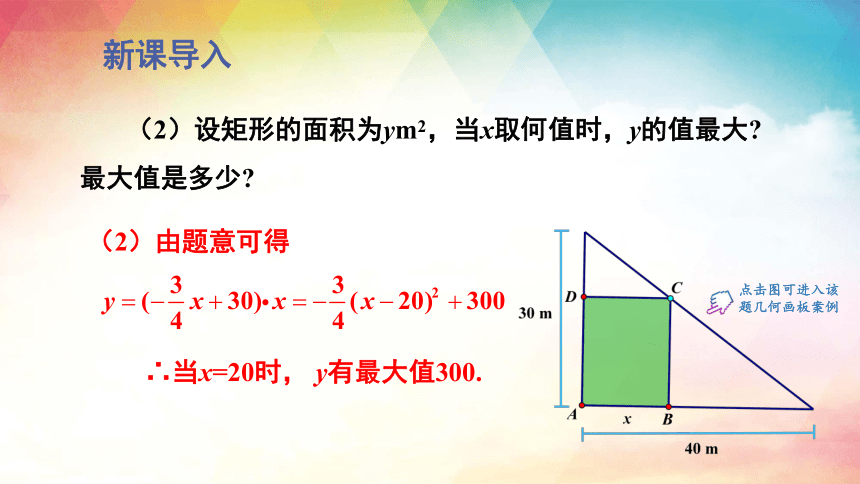
(2)设矩形的面积为ym2,当x取何值时,y的值最大 最大值是多少
(2)由题意可得
∴当x=20时, y有最大值300.
点击图可进入该题几何画板案例
探究新知
在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
点击图可进入该题几何画板案例
N
M
解:如下图所示,过点G作GM⊥EF,交DA于点N,交CB于点M.
∵ DA//CB,∴GN⊥DA.
∵DA//EF,
点击图可进入该题几何画板案例
N
M
探究新知
在Rt△EGF中,
由
得GM=24(m)
∴当x=12时, y有最大值300.
例1 某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多 (结果精确到0.01m)此时,窗户的面积是多少 (结果精确到0.01m2)
解:∵7x+4y+πx=15,
∴
∵0<x<15,且0< <15,
∴0<x<1.48.
设窗户的面积是Sm2,则
∴当x= ≈1.07时,S最大= ≈4.02.
因此,当x约为1.07m时,窗户通过的光线最多.
此时,窗户的面积约为4.02m2.
随堂练习
1. 一根铝合金型材长为6m,用它制作一个“日”字形窗户的框架ABCD(如图),如果恰好用完整条铝合金型材,那么AB,AD分别为多少米时,窗户的面积最大?
A
B
C
D
解:设AB=x,则AD= ,
∴S=
∴当x=1时,S有最大值 .
即当AB,AD分别为1m,1.5m时,窗户面积最大,为1.5m2.
2. 如图,小亮父亲想用长为80m的栅栏,再借助房屋的外墙围成一个矩形羊圈ABCD,已知房屋外墙长50m,设矩形ABCD的边 AB = x m,面积为 S m2.
A
B
C
D
(1)写出 S 与 x 之间的关系式,并指出 x 的取值范围;
解:(1)S=x·(80-2x)=-2x2+80x
由题意0<80-2x≤50
∴15≤ x<40
x
2. 如图,小亮父亲想用长为80m的栅栏,再借助房屋的外墙围成一个矩形羊圈ABCD,已知房屋外墙长50m,设矩形ABCD的边 AB = x m,面积为 S m2.
A
B
C
D
(2)S=x·(80-2x)=-2x2+80x
=-2(x-20)2+800
∴当x=20时, S 有最大值800.
即当AB,BC分别为20m,40m时,羊圈面积最大,为800m2.
(2)当 AB, BC 分别为多少米时,羊圈的面积最大 最大面积是多少
x
3. 在前面的问题中,如果设AD边的长为xm,那么问题的结果会怎样?
E
F
解:∵AD=xm,DC∥AB,
∴ ,
∴DC=AB= ,
∴y=AD·AB=
=
(0<x<30)
∴当x=15时, y有最大值300.
4 二次函数的应用
第2课时 最大利润问题
北师版九年级数学下册
第二章 二次函数
新课导入
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
选择什么量设未知数呢?
销售利润=单件利润×销售量
遇到有关销售利润的问题,常用相等关系是?
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
x
新课导入
单件利润为:(x-10)元
降价后的销售量为: 件
y
=-5000(x-12)2+20000
故厂家批发单价为12元时,获利最多,为20000元.
新课导入
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
每件T恤衫降价a元
y
单件利润为:(13-a-10)元
降价后的销售量为: 件
=-5000(a-1)2+20000
故厂家批发单价为12元时,获利最多,为20000元.
13-1=12(元),
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
新课导入
你还有其他设未知量的方法吗?
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
新课导入
解决了上述关于服装销售的问题,请你谈一谈怎样设因变量更好?
探究新知
例2 某旅馆有客房 120 间,每间房的日租金为 160 元时,每天都客满. 经市场调查发现,如果每间客房的日租金增加 10 元,那么客房每天出租数会减少 6 间.不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高 最高总收入是多少
客房日租金的总收入=每间客房日租金×每天客房出租数
探究新知
例2 某旅馆有客房 120 间,每间房的日租金为 160 元时,每天都客满. 经市场调查发现,如果每间客房的日租金增加 10 元,那么客房每天出租数会减少 6 间.不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高 最高总收入是多少
设每间客房的日租金提高x个10元
则每天客房数会减少6x间
客房日租金总收入为y元
探究新知
∵ x ≥ 0,且120-6x>0,∴ 0 ≤ x<20.
当x=2时, y最大=19440.
这时每间客房的日租金为160+10×2= 180 (元)
因此,每间客房的日租金提高到 180 元时,客房总收入最高, 最高收入为19440 元.
议一议
还记得本章一开始的“种多少棵橙子树”的问题吗?我们得到表示增种橙子树的数量x(棵)与橙子总产量y(个)的二次函数表达式
(1)利用函数图象描述橙子的总产量与增种橙子树的棵树之间的关系.
(2)增种多少棵橙子树,可以使橙子的总产量在60400个以上?
∴ 增种6~14棵橙子树可以使橙子的总产量在60400个以上.
随堂练习
1. 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可售出400件. 根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件. 销售单价为多少元时,半月内获得的利润最大?最大利润是多少?
解:设销售单价为x元(x≥30),利润为y元,则
y = (x-20)[400-20(x-20)] =-20(x-35)2+4500
∴当x=35时, y最大=4500.
即销售单价为35元时,半月内可获得最大利润4500元.
2. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅行团每增加一人,每人的单价就降低10元.你能帮助算一下,当一个旅行团的人数是多少时,旅行社可以获得最大营业额 最大营业额是多少
解:设一个旅行团有x人时,旅行社营业额为y元.则
y = [800-10(x-30)]·x =-10x2+1100x
= -10(x-55)2+30250
∴当x=55时, y最大=30250.
即一个旅行团有55人时,旅行社可获最大利润30250元.
3. 某种文化衫,平均每天销售 40件,平均每件盈利20 元,若每件降价1元, 则每天可多售10件,如果每天要盈利最多,每件应降价多少元?
解:设每件应降价x元,每天的利润为y元,
由题意得:y=(20-x)(40+10x)
=-10x2+160x+800
=-10(x-8)2+1440 (0<x<20).
当x=8时,y有最大值1440.
即当每件降价8元时,每天的盈利最多.
谢谢观看
4 二次函数的应用
第1课时 最大面积问题
北师版九年级数学下册
第二章 二次函数
新课导入
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
(1)如果设矩形的一边AB=x m,那么
AD边的长度如何表示
解:(1)设AD=h,由图可知Rt△EDC∽Rt△CBF
∴
∴
新课导入
E
F
新课导入
(2)设矩形的面积为ym2,当x取何值时,y的值最大 最大值是多少
(2)由题意可得
∴当x=20时, y有最大值300.
点击图可进入该题几何画板案例
探究新知
在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
点击图可进入该题几何画板案例
N
M
解:如下图所示,过点G作GM⊥EF,交DA于点N,交CB于点M.
∵ DA//CB,∴GN⊥DA.
∵DA//EF,
点击图可进入该题几何画板案例
N
M
探究新知
在Rt△EGF中,
由
得GM=24(m)
∴当x=12时, y有最大值300.
例1 某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多 (结果精确到0.01m)此时,窗户的面积是多少 (结果精确到0.01m2)
解:∵7x+4y+πx=15,
∴
∵0<x<15,且0< <15,
∴0<x<1.48.
设窗户的面积是Sm2,则
∴当x= ≈1.07时,S最大= ≈4.02.
因此,当x约为1.07m时,窗户通过的光线最多.
此时,窗户的面积约为4.02m2.
随堂练习
1. 一根铝合金型材长为6m,用它制作一个“日”字形窗户的框架ABCD(如图),如果恰好用完整条铝合金型材,那么AB,AD分别为多少米时,窗户的面积最大?
A
B
C
D
解:设AB=x,则AD= ,
∴S=
∴当x=1时,S有最大值 .
即当AB,AD分别为1m,1.5m时,窗户面积最大,为1.5m2.
2. 如图,小亮父亲想用长为80m的栅栏,再借助房屋的外墙围成一个矩形羊圈ABCD,已知房屋外墙长50m,设矩形ABCD的边 AB = x m,面积为 S m2.
A
B
C
D
(1)写出 S 与 x 之间的关系式,并指出 x 的取值范围;
解:(1)S=x·(80-2x)=-2x2+80x
由题意0<80-2x≤50
∴15≤ x<40
x
2. 如图,小亮父亲想用长为80m的栅栏,再借助房屋的外墙围成一个矩形羊圈ABCD,已知房屋外墙长50m,设矩形ABCD的边 AB = x m,面积为 S m2.
A
B
C
D
(2)S=x·(80-2x)=-2x2+80x
=-2(x-20)2+800
∴当x=20时, S 有最大值800.
即当AB,BC分别为20m,40m时,羊圈面积最大,为800m2.
(2)当 AB, BC 分别为多少米时,羊圈的面积最大 最大面积是多少
x
3. 在前面的问题中,如果设AD边的长为xm,那么问题的结果会怎样?
E
F
解:∵AD=xm,DC∥AB,
∴ ,
∴DC=AB= ,
∴y=AD·AB=
=
(0<x<30)
∴当x=15时, y有最大值300.
4 二次函数的应用
第2课时 最大利润问题
北师版九年级数学下册
第二章 二次函数
新课导入
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
选择什么量设未知数呢?
销售利润=单件利润×销售量
遇到有关销售利润的问题,常用相等关系是?
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
x
新课导入
单件利润为:(x-10)元
降价后的销售量为: 件
y
=-5000(x-12)2+20000
故厂家批发单价为12元时,获利最多,为20000元.
新课导入
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
每件T恤衫降价a元
y
单件利润为:(13-a-10)元
降价后的销售量为: 件
=-5000(a-1)2+20000
故厂家批发单价为12元时,获利最多,为20000元.
13-1=12(元),
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
新课导入
你还有其他设未知量的方法吗?
服装厂生产某品牌的T恤衫成本是每件 10 元.根据市场调查,以单价13元批发给经销商,经销商愿意经销 5000件 ,并且表示单价每降价 0.1 元,愿意多经销 500 件.
请你帮助分析,厂家批发单价是多少时可以获利最多
新课导入
解决了上述关于服装销售的问题,请你谈一谈怎样设因变量更好?
探究新知
例2 某旅馆有客房 120 间,每间房的日租金为 160 元时,每天都客满. 经市场调查发现,如果每间客房的日租金增加 10 元,那么客房每天出租数会减少 6 间.不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高 最高总收入是多少
客房日租金的总收入=每间客房日租金×每天客房出租数
探究新知
例2 某旅馆有客房 120 间,每间房的日租金为 160 元时,每天都客满. 经市场调查发现,如果每间客房的日租金增加 10 元,那么客房每天出租数会减少 6 间.不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高 最高总收入是多少
设每间客房的日租金提高x个10元
则每天客房数会减少6x间
客房日租金总收入为y元
探究新知
∵ x ≥ 0,且120-6x>0,∴ 0 ≤ x<20.
当x=2时, y最大=19440.
这时每间客房的日租金为160+10×2= 180 (元)
因此,每间客房的日租金提高到 180 元时,客房总收入最高, 最高收入为19440 元.
议一议
还记得本章一开始的“种多少棵橙子树”的问题吗?我们得到表示增种橙子树的数量x(棵)与橙子总产量y(个)的二次函数表达式
(1)利用函数图象描述橙子的总产量与增种橙子树的棵树之间的关系.
(2)增种多少棵橙子树,可以使橙子的总产量在60400个以上?
∴ 增种6~14棵橙子树可以使橙子的总产量在60400个以上.
随堂练习
1. 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可售出400件. 根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件. 销售单价为多少元时,半月内获得的利润最大?最大利润是多少?
解:设销售单价为x元(x≥30),利润为y元,则
y = (x-20)[400-20(x-20)] =-20(x-35)2+4500
∴当x=35时, y最大=4500.
即销售单价为35元时,半月内可获得最大利润4500元.
2. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅行团每增加一人,每人的单价就降低10元.你能帮助算一下,当一个旅行团的人数是多少时,旅行社可以获得最大营业额 最大营业额是多少
解:设一个旅行团有x人时,旅行社营业额为y元.则
y = [800-10(x-30)]·x =-10x2+1100x
= -10(x-55)2+30250
∴当x=55时, y最大=30250.
即一个旅行团有55人时,旅行社可获最大利润30250元.
3. 某种文化衫,平均每天销售 40件,平均每件盈利20 元,若每件降价1元, 则每天可多售10件,如果每天要盈利最多,每件应降价多少元?
解:设每件应降价x元,每天的利润为y元,
由题意得:y=(20-x)(40+10x)
=-10x2+160x+800
=-10(x-8)2+1440 (0<x<20).
当x=8时,y有最大值1440.
即当每件降价8元时,每天的盈利最多.
谢谢观看
