【核心素养目标】苏科版八年级数学上册2.5 第4课时 直角三角形的性质 课件 (共23张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版八年级数学上册2.5 第4课时 直角三角形的性质 课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 885.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 19:38:49 | ||
图片预览








文档简介
(共23张PPT)
第2章 对称图形
2.5 等腰三角形的轴对称性
第4课时 直角三角形的性质
1.探索并掌握直角三角形斜边上的中线等于斜边的一半.
2.探索并掌握有一个角为30°的直角三角形的性质.
3.理解合情推理和演绎推理都是获得数学结论的重要途径,经历分析法演绎证明思路的过程.
◎重点:探索并应用“直角三角形斜边上的中线等于斜边的一半”解决相关数学问题.
◎难点:引导学生用“分析法”证明“直角三角形斜边上的中线等于斜边的一半”.
同学们在作图时候,经常要用到三角板,大家看一下手里的三角板,你知道直角三角形斜边上的中线和斜边之间有什么关系吗?
1.剪一张直角三角形纸片,把纸片按下图所示方法折叠,你有什么发现?
结论:直角三角形斜边上的中线等于 斜边的一半 .
斜边的一半
直角三角形的性质
阅读课本本课时从开始到“练习”前面内容,回答下面问题:
·导学建议·
让学生动手操作得到直角三角形斜边上的中线和斜边之间的长度关系,教师通过引导学生动手操作激发学生的学习兴趣.
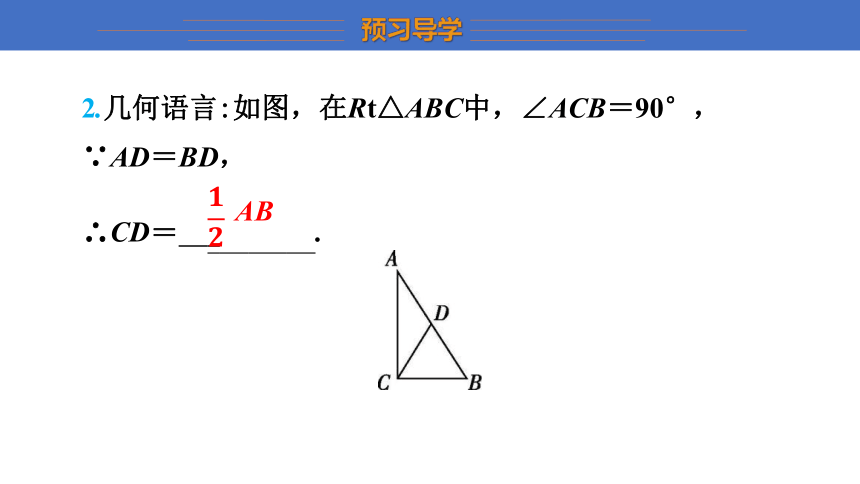
2.几何语言:如图,在Rt△ABC中,∠ACB=90°,
∵AD=BD,
∴CD= AB .
AB
3.在Rt△ABC中,如果∠ACB是直角,∠A=30°,那么BC和AB有怎样的数量关系?我们可以得到什么结论?
答:BC=AB.
结论:在直角三角形中,如果一个锐角等于30°,那么它所对应的直角边等于斜边的一半.
1.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,E为AC的中点.连接DE,则△CDE的周长为( C )
A.20 B.12
C.14 D.13
C
2.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( C )
A.60° B.45°
C.30° D.75°
C
3.如图,这是屋架设计图的一部分,D是斜梁AB的中点,立柱BC,DE分别垂直于横梁AC,若DE=1.8 m,∠A=30°,则斜梁AB的长为 7.2 m.
7.2
4.如图,在△ABC中,∠ACB=90°,∠B=20°,D在BC上,AD=BD,E为AB的中点,AD,CE相交于点F,则∠DFE= 60° .
60°
直角三角形的性质应用于几何计算
1.如图,∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则ON=( A )
A.7 B.6
C.5 D.4
A
直角三角形的性质应用于几何证明
2.如图,在△ABC中,BD,CE是高,G为BC的中点,FG⊥DE,F为垂足,求证:EF=DF.
证明:如图,连接EG、DG,
∵G为BC的中点,BD,CE是高,
∴EG=DG=BC.
∵FG⊥DE,
∴EF=DF.
·导学建议·
学生自主分析,请学生代表分析思路,其基本思路为连续两次运用“直角三角形斜边上的中线等于斜边的一半”.
直角三角形的性质应用于实际问题
3.如图,一根5米的竹竿AB斜靠在竖直的墙上,P是AB的中点,A'B'表示竹竿AB端沿墙上下滑动过程的某个位置,那么在竹竿AB的滑动过程中,OP是否发生变化?如果发生变化,请计算OP变化了多少米?如果不发生变化,请说明理由.
解:OP的长度不发生变化.
理由:∵AO⊥BO,P是AB的中点,
∴在Rt△AOB中,OP=AB=2.5.
∵A'O⊥B'O,P'是A'B'的中点,
∴在Rt△A'OB'中,OP'=A'B'=2.5,
∴OP=OP',
∴在滑动的过程中,OP的长度不发生变化.
·导学建议·
引导学生运用“直角三角形斜边上的中线等于斜边的一半”,OP、OP'分别是Rt△AOB与Rt△A'OB'斜边上的中线,分别等于斜边AB和A'B'的一半.
1.如图,在△ABC中,∠C=90°,∠A=15°,∠DBC=60°,BC=4,则AD的长是( D )
A.2 B.4
C.6 D.8
D
2.如图,在Rt△ABC中,CD是斜边AB上的中线,DE⊥AC,垂足为E.如果CD=2.4 cm,那么AB= 4.8 cm.
4.8
3.如图,要修建一个地铁站,想把地铁站的出口D建造在离附近的三个公交站点A、B、C的距离相等的位置.而这三个公交站点的位置正好构成一个直角三角形,∠ACB=90°.你会把地铁站的出口D建造在哪里?
解:根据“直角三角形斜边上的中线等于斜边的一半”可知,地铁站的出口D应建在AB的中点上,如图所示.
解:根据“直角三角形斜边上的中线等于斜边的一半”可
知,地铁站的出口D应建在AB的中点上,如图所示.
第2章 对称图形
2.5 等腰三角形的轴对称性
第4课时 直角三角形的性质
1.探索并掌握直角三角形斜边上的中线等于斜边的一半.
2.探索并掌握有一个角为30°的直角三角形的性质.
3.理解合情推理和演绎推理都是获得数学结论的重要途径,经历分析法演绎证明思路的过程.
◎重点:探索并应用“直角三角形斜边上的中线等于斜边的一半”解决相关数学问题.
◎难点:引导学生用“分析法”证明“直角三角形斜边上的中线等于斜边的一半”.
同学们在作图时候,经常要用到三角板,大家看一下手里的三角板,你知道直角三角形斜边上的中线和斜边之间有什么关系吗?
1.剪一张直角三角形纸片,把纸片按下图所示方法折叠,你有什么发现?
结论:直角三角形斜边上的中线等于 斜边的一半 .
斜边的一半
直角三角形的性质
阅读课本本课时从开始到“练习”前面内容,回答下面问题:
·导学建议·
让学生动手操作得到直角三角形斜边上的中线和斜边之间的长度关系,教师通过引导学生动手操作激发学生的学习兴趣.
2.几何语言:如图,在Rt△ABC中,∠ACB=90°,
∵AD=BD,
∴CD= AB .
AB
3.在Rt△ABC中,如果∠ACB是直角,∠A=30°,那么BC和AB有怎样的数量关系?我们可以得到什么结论?
答:BC=AB.
结论:在直角三角形中,如果一个锐角等于30°,那么它所对应的直角边等于斜边的一半.
1.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,E为AC的中点.连接DE,则△CDE的周长为( C )
A.20 B.12
C.14 D.13
C
2.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( C )
A.60° B.45°
C.30° D.75°
C
3.如图,这是屋架设计图的一部分,D是斜梁AB的中点,立柱BC,DE分别垂直于横梁AC,若DE=1.8 m,∠A=30°,则斜梁AB的长为 7.2 m.
7.2
4.如图,在△ABC中,∠ACB=90°,∠B=20°,D在BC上,AD=BD,E为AB的中点,AD,CE相交于点F,则∠DFE= 60° .
60°
直角三角形的性质应用于几何计算
1.如图,∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则ON=( A )
A.7 B.6
C.5 D.4
A
直角三角形的性质应用于几何证明
2.如图,在△ABC中,BD,CE是高,G为BC的中点,FG⊥DE,F为垂足,求证:EF=DF.
证明:如图,连接EG、DG,
∵G为BC的中点,BD,CE是高,
∴EG=DG=BC.
∵FG⊥DE,
∴EF=DF.
·导学建议·
学生自主分析,请学生代表分析思路,其基本思路为连续两次运用“直角三角形斜边上的中线等于斜边的一半”.
直角三角形的性质应用于实际问题
3.如图,一根5米的竹竿AB斜靠在竖直的墙上,P是AB的中点,A'B'表示竹竿AB端沿墙上下滑动过程的某个位置,那么在竹竿AB的滑动过程中,OP是否发生变化?如果发生变化,请计算OP变化了多少米?如果不发生变化,请说明理由.
解:OP的长度不发生变化.
理由:∵AO⊥BO,P是AB的中点,
∴在Rt△AOB中,OP=AB=2.5.
∵A'O⊥B'O,P'是A'B'的中点,
∴在Rt△A'OB'中,OP'=A'B'=2.5,
∴OP=OP',
∴在滑动的过程中,OP的长度不发生变化.
·导学建议·
引导学生运用“直角三角形斜边上的中线等于斜边的一半”,OP、OP'分别是Rt△AOB与Rt△A'OB'斜边上的中线,分别等于斜边AB和A'B'的一半.
1.如图,在△ABC中,∠C=90°,∠A=15°,∠DBC=60°,BC=4,则AD的长是( D )
A.2 B.4
C.6 D.8
D
2.如图,在Rt△ABC中,CD是斜边AB上的中线,DE⊥AC,垂足为E.如果CD=2.4 cm,那么AB= 4.8 cm.
4.8
3.如图,要修建一个地铁站,想把地铁站的出口D建造在离附近的三个公交站点A、B、C的距离相等的位置.而这三个公交站点的位置正好构成一个直角三角形,∠ACB=90°.你会把地铁站的出口D建造在哪里?
解:根据“直角三角形斜边上的中线等于斜边的一半”可知,地铁站的出口D应建在AB的中点上,如图所示.
解:根据“直角三角形斜边上的中线等于斜边的一半”可
知,地铁站的出口D应建在AB的中点上,如图所示.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
