实际问题与一元一次方程(行程问题)
文档属性
| 名称 | 实际问题与一元一次方程(行程问题) |

|
|
| 格式 | rar | ||
| 文件大小 | 34.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-28 00:00:00 | ||
图片预览




文档简介
课件11张PPT。3.4 实际问题与一元一次方程(4)行程问题例1.甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.①几小时后两车相遇?分析:若两车同时出发,则等量关系为:
吉普车的路程+客车的路程=1500解:设两车x小时后相遇,依题意可得
60x+(60÷1.5)x=1500
解得:x=15
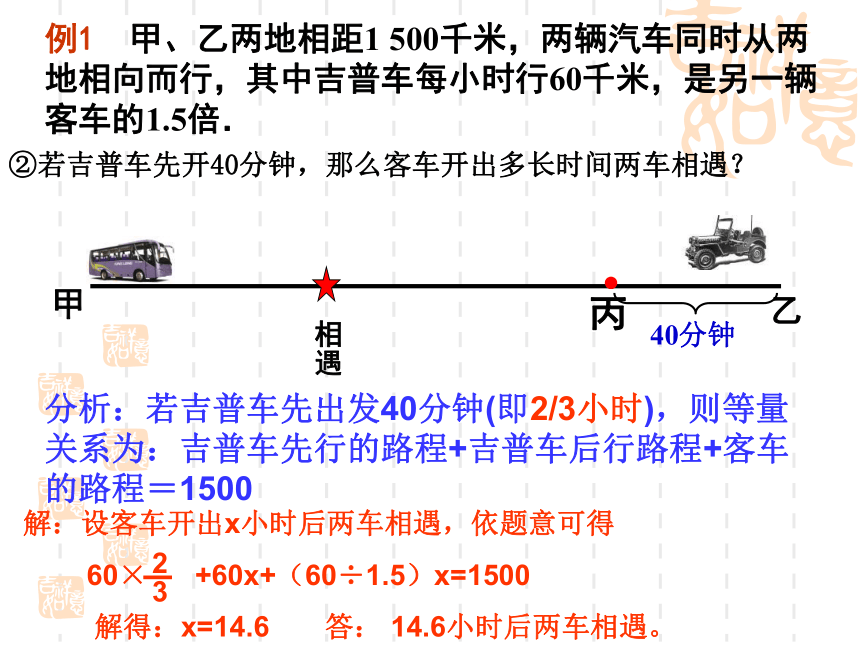
答:15小时后两车相遇。 ②若吉普车先开40分钟,那么客车开出多长时间两车相遇? 例1 甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.②若吉普车先开40分钟,那么客车开出多长时间两车相遇? 分析:若吉普车先出发40分钟(即2/3小时),则等量关系为:吉普车先行的路程+吉普车后行路程+客车的路程=1500例2、甲骑自行车从A地到B地,乙骑自行车从B地到A地,两人都匀速前进。已知两人在上午8时同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米。求A、B两地间的路程。解法2:设甲、乙两人的速度和为x千米/小时,则A、B两地间
路程为(2x+36)千米,而10时到12时,两人的路程和
为 2×36=72千米,故可得2x=72
解得:x=36
所以,2x+36=108
答:A、B两地相距108千米。例3、某船从A码头顺流而下到B码头,然后逆流返回C码头(C码头在A、B之间),共行9小时,已知船在静水中的速度为7.5千米/时,水流速度是2.5千米/时,A、C两码头相距15千米,求A、B之间的距离.分析:船在顺水中的速度为(7.5+2.5)千米/小时,船在逆水中的速度为(7.5-2.5)千米/小时,等量关系:
船从A到B花的时间(顺水)+船从B到C的时间(逆水)=9例4.一小船由A港口到B港口顺流需行驶6小时,由B港口到A港口需行驶8小时,一天,小船由A港口出发顺流到达B港口,发现一救生圈中途落水,立即返回,1小时后找到救生圈,若水流速度是2千米/时。(1)小船在静水中的速度是多少?(2)救生圈是何时掉入水中的? 常用的关系式
顺流时的速度=静水中的速度+水流的速度
逆流时的速度=静水中的速度-水流的速度解:(1)假设小船在静水中的速度是x千米/时 则有 6×(x+2)=8×(x-2) x=14 所以小船在静水中的速度是14千米/时
(2)假设救生圈是在离开A港y小时的时候落水的,
则有
2×(6-y+1)+(14-2)×1=(6-y)×(14+2) 解得y=5.
所以救生圈是在离开A港5小时的地方掉入水中的。
解释:6-y+1为救生圈在水中漂的时间,再乘以2就是找到救生圈的时候它所漂过的路程,(14-2)×1为船回来时走的路程,这两段路程相加就是救生圈掉落地点到B港的距离 例5、从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?解:设水路长为x千米,则公路长为(x+40)千米等量关系:船行时间-车行时间=3小时答:水路长240千米,公路长为280千米,车行时间为
7小时,船行时间为10小时 依题意得:
x=240例6、甲、乙两人在400米长的环形跑道上练习跑步,甲每秒跑5米,乙每秒跑3米。(1)若两人同时同地同向出发,多长时间两人首次相遇?(2)若两人同时同地反向出发,多长时间两人首次相遇?分析:圆形跑道中的规律:
第1次相遇:快的人跑的路程-慢的人跑的路程=1圈
第2次相遇: 快的人跑的路程-慢的人跑的路程=2圈
(第3次相遇:快的人跑的路程-慢的人跑的路程=3圈
………. 等量关系
甲行的路程-乙行的路程=400米 等量关系
甲行的路程+乙行的路程=400米一、明确行程问题中三个量的关系三个基本量关系是:速度×时间=路程分析方法辅助手段:线型图示法 二、追及问题:
(1)同地不同时:慢者行程+先行路程=快者路程(2)同时不同地:快者路程 — 慢者行程=间隔距离行程问题
吉普车的路程+客车的路程=1500解:设两车x小时后相遇,依题意可得
60x+(60÷1.5)x=1500
解得:x=15
答:15小时后两车相遇。 ②若吉普车先开40分钟,那么客车开出多长时间两车相遇? 例1 甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.②若吉普车先开40分钟,那么客车开出多长时间两车相遇? 分析:若吉普车先出发40分钟(即2/3小时),则等量关系为:吉普车先行的路程+吉普车后行路程+客车的路程=1500例2、甲骑自行车从A地到B地,乙骑自行车从B地到A地,两人都匀速前进。已知两人在上午8时同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米。求A、B两地间的路程。解法2:设甲、乙两人的速度和为x千米/小时,则A、B两地间
路程为(2x+36)千米,而10时到12时,两人的路程和
为 2×36=72千米,故可得2x=72
解得:x=36
所以,2x+36=108
答:A、B两地相距108千米。例3、某船从A码头顺流而下到B码头,然后逆流返回C码头(C码头在A、B之间),共行9小时,已知船在静水中的速度为7.5千米/时,水流速度是2.5千米/时,A、C两码头相距15千米,求A、B之间的距离.分析:船在顺水中的速度为(7.5+2.5)千米/小时,船在逆水中的速度为(7.5-2.5)千米/小时,等量关系:
船从A到B花的时间(顺水)+船从B到C的时间(逆水)=9例4.一小船由A港口到B港口顺流需行驶6小时,由B港口到A港口需行驶8小时,一天,小船由A港口出发顺流到达B港口,发现一救生圈中途落水,立即返回,1小时后找到救生圈,若水流速度是2千米/时。(1)小船在静水中的速度是多少?(2)救生圈是何时掉入水中的? 常用的关系式
顺流时的速度=静水中的速度+水流的速度
逆流时的速度=静水中的速度-水流的速度解:(1)假设小船在静水中的速度是x千米/时 则有 6×(x+2)=8×(x-2) x=14 所以小船在静水中的速度是14千米/时
(2)假设救生圈是在离开A港y小时的时候落水的,
则有
2×(6-y+1)+(14-2)×1=(6-y)×(14+2) 解得y=5.
所以救生圈是在离开A港5小时的地方掉入水中的。
解释:6-y+1为救生圈在水中漂的时间,再乘以2就是找到救生圈的时候它所漂过的路程,(14-2)×1为船回来时走的路程,这两段路程相加就是救生圈掉落地点到B港的距离 例5、从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?解:设水路长为x千米,则公路长为(x+40)千米等量关系:船行时间-车行时间=3小时答:水路长240千米,公路长为280千米,车行时间为
7小时,船行时间为10小时 依题意得:
x=240例6、甲、乙两人在400米长的环形跑道上练习跑步,甲每秒跑5米,乙每秒跑3米。(1)若两人同时同地同向出发,多长时间两人首次相遇?(2)若两人同时同地反向出发,多长时间两人首次相遇?分析:圆形跑道中的规律:
第1次相遇:快的人跑的路程-慢的人跑的路程=1圈
第2次相遇: 快的人跑的路程-慢的人跑的路程=2圈
(第3次相遇:快的人跑的路程-慢的人跑的路程=3圈
………. 等量关系
甲行的路程-乙行的路程=400米 等量关系
甲行的路程+乙行的路程=400米一、明确行程问题中三个量的关系三个基本量关系是:速度×时间=路程分析方法辅助手段:线型图示法 二、追及问题:
(1)同地不同时:慢者行程+先行路程=快者路程(2)同时不同地:快者路程 — 慢者行程=间隔距离行程问题
