人教版六年级下册数学圆锥的体积(课件)(共32张PPT)
文档属性
| 名称 | 人教版六年级下册数学圆锥的体积(课件)(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-31 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
圆锥的体积
圆柱与圆锥
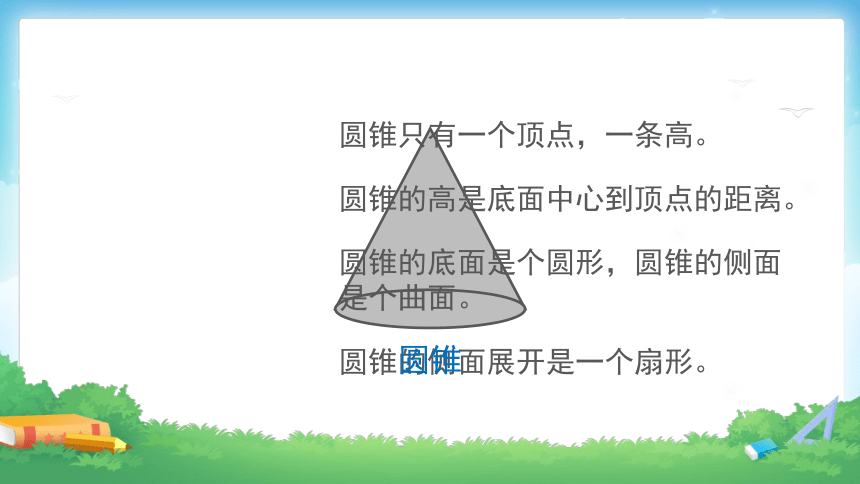
圆锥的侧面展开是一个扇形。
圆锥
圆锥只有一个顶点,一条高。
圆锥的高是底面中心到顶点的距离。
圆锥的底面是个圆形,圆锥的侧面是个曲面。
VS
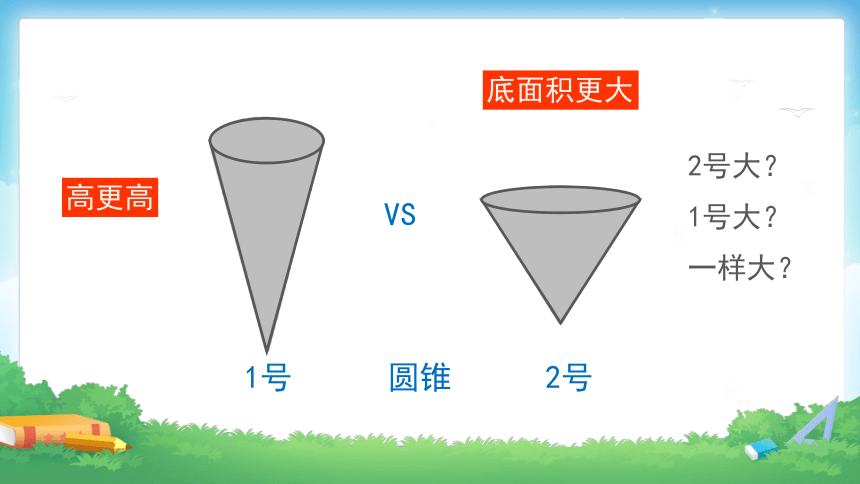
1号
2号
底面积更大
高更高
2号大?
1号大?
一样大?
圆锥
圆锥的体积
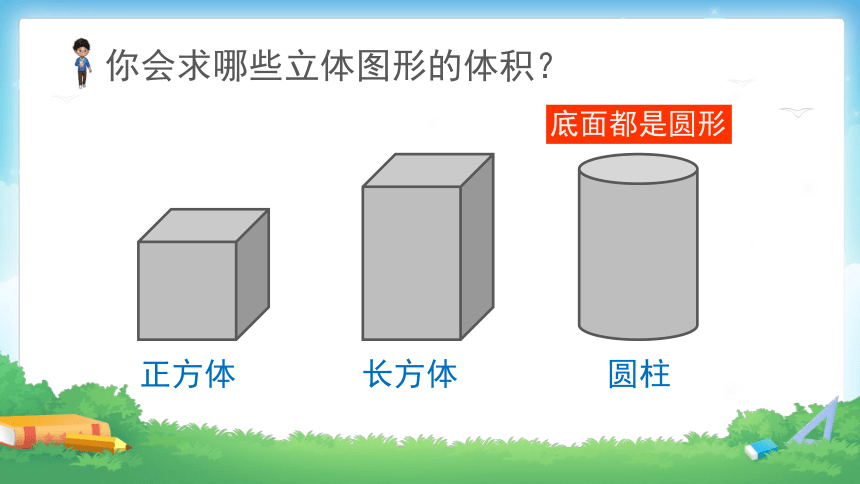
正方体
长方体
圆柱
底面都是圆形
你会求哪些立体图形的体积?
课堂实验
圆锥和圆柱的体积之间是否存在关系?
存在怎样的关系?
实验验证
小组分工合作。
根据记录单的要求做实验。
实验完成后,认真填写记录单。
注意实验卫生。
实验要求
实验一:拿出1号学具,在空圆锥里装满沙子倒入圆柱里( )次倒满。
实验二:拿出2号学具,在空圆锥里装满沙子倒入圆柱里( )次倒满。
3
3
3
7
2
10
?
?
实验记录单
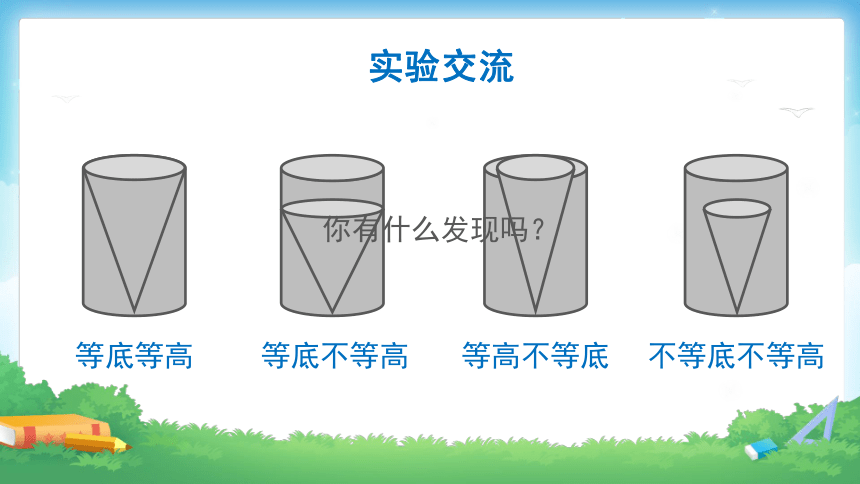
等底等高
等底不等高
等高不等底
不等底不等高
你有什么发现吗?
实验交流
实验猜想
等底等高
实验一:拿出1号学具,在空圆锥里装满沙子倒入圆柱里( )次倒满。
3
3
3
圆柱的体积是圆锥体积的3倍,
圆锥的体积是圆柱体积的 。
等底等高的情况下,
实验结论
等底等高的圆柱和圆锥,
圆柱的体积是圆锥体积的3倍,
圆锥的体积是圆柱体积的 。
实验验证
等底等高
素材来源网络,如有侵权请联系我们!
实验验证
等底等高
实验验证
等底等高
1
存在误差
圆柱的体积是圆锥体积的3倍,
圆锥的体积是圆柱体积的 。
等底等高的圆柱和圆锥
圆锥的体积公式
圆锥的体积 = ×
底面积×高
圆柱的体积 ×
V圆锥 =
V圆柱
×
圆锥的体积 =
sh
=
圆锥的底面积
s
与圆锥等底等高的圆柱的底面积
圆锥的高
与圆锥等底等高的圆柱的高
h
1、 圆柱和圆锥,
圆柱的体积是 ,
圆锥的体积是 。
等底等高的
圆柱体积的
圆锥体积的3倍
2、圆锥的体积公式 ,
s表示 ,
h表示 。
圆锥的高
圆锥的底面积
V = sh
课堂练习
1、一个圆柱的体积是30立方米,与它等底等高的圆锥的体积是( )立方米。
2、一个圆锥的体积是30立方米,与它等底等高的圆柱的体积是( )立方米。
10
90
V圆锥 = V圆柱× = 30× = 10m
V圆柱 = V圆锥×3 = 30×3 = 90m
填一填
1、圆锥的体积等于圆柱体积的三分之一。………( )
2、圆柱体的体积一定比圆锥体的体积大。………( )
3、一个圆锥与一个圆柱等底等高,已知圆锥
的体积是8立方米,圆柱的体积是24立方米。……( )
判断一下
×
×
√
题目没有说在等底等高的情况下
缺少必要数据:底面积和高
V圆柱 = V圆锥×3 =8×3=24m
解决问题
这两根冰淇淋的体积各是多少?哪根大呢?
1号
2号
底面积:
12.56cm2
高:
9cm
底面积:
28.26c㎡
高:
6cm
V = sh
= ×12.56×9
= 37.68cm
①号
V = sh
= ×28.26×6
= 56.52cm
②号
37.68cm < 56.52cm
答:1号冰淇淋的体积是37.68cm ,
2号冰淇淋的体积是56.52cm ,
所以2号冰淇淋大。
同学1
V = sh
= ×12.56×9
= ×9×12.56
= 3×12.56
= 37.68cm
V = sh
= ×28.26×6
= ×6×28.26
= 2×28.26
= 56.52cm
37.68cm < 56.52cm
答:1号冰淇淋的体积是37.68cm ,
2号是56.52cm ,2号大。
同学2
①
②
进行约分
解决问题
工地上有一堆沙子,近似于一个圆锥(如下图)。
这堆沙子的体积大约是多少?
V = sh
= ×[(4÷2) ×3.14]×1.2
= ×12.56×1.2
= ×1.2×12.56
= 5.024(m )
答:这堆沙子的体积大约是5.024m 。
同学1
V = sh
= ×3.14×2×1.2
= 3.14×0.8
= 28.26(m )
r = 4÷2=2(m)
答:这堆沙子的体积大约是2.826m 。
同学2
√
5.024(m )
r = 4÷2=2(m)
V = sh
= ×3.14×2×1.2
= 3.14×0.8
= 28.26(m )
s = πr
√
√
V = s h
没有乘平方
课堂小结
等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的三倍。
你有什么
收获吗?
等底等高的圆柱和圆锥,圆锥的体积是圆柱体积的 。
V圆锥 =
V圆柱
sh
=
圆锥的体积公式
只要你们多思、多想、多动,你们就可以自主探索出更多有趣的数学知识。
再 见!
圆锥的体积
圆柱与圆锥
圆锥的侧面展开是一个扇形。
圆锥
圆锥只有一个顶点,一条高。
圆锥的高是底面中心到顶点的距离。
圆锥的底面是个圆形,圆锥的侧面是个曲面。
VS
1号
2号
底面积更大
高更高
2号大?
1号大?
一样大?
圆锥
圆锥的体积
正方体
长方体
圆柱
底面都是圆形
你会求哪些立体图形的体积?
课堂实验
圆锥和圆柱的体积之间是否存在关系?
存在怎样的关系?
实验验证
小组分工合作。
根据记录单的要求做实验。
实验完成后,认真填写记录单。
注意实验卫生。
实验要求
实验一:拿出1号学具,在空圆锥里装满沙子倒入圆柱里( )次倒满。
实验二:拿出2号学具,在空圆锥里装满沙子倒入圆柱里( )次倒满。
3
3
3
7
2
10
?
?
实验记录单
等底等高
等底不等高
等高不等底
不等底不等高
你有什么发现吗?
实验交流
实验猜想
等底等高
实验一:拿出1号学具,在空圆锥里装满沙子倒入圆柱里( )次倒满。
3
3
3
圆柱的体积是圆锥体积的3倍,
圆锥的体积是圆柱体积的 。
等底等高的情况下,
实验结论
等底等高的圆柱和圆锥,
圆柱的体积是圆锥体积的3倍,
圆锥的体积是圆柱体积的 。
实验验证
等底等高
素材来源网络,如有侵权请联系我们!
实验验证
等底等高
实验验证
等底等高
1
存在误差
圆柱的体积是圆锥体积的3倍,
圆锥的体积是圆柱体积的 。
等底等高的圆柱和圆锥
圆锥的体积公式
圆锥的体积 = ×
底面积×高
圆柱的体积 ×
V圆锥 =
V圆柱
×
圆锥的体积 =
sh
=
圆锥的底面积
s
与圆锥等底等高的圆柱的底面积
圆锥的高
与圆锥等底等高的圆柱的高
h
1、 圆柱和圆锥,
圆柱的体积是 ,
圆锥的体积是 。
等底等高的
圆柱体积的
圆锥体积的3倍
2、圆锥的体积公式 ,
s表示 ,
h表示 。
圆锥的高
圆锥的底面积
V = sh
课堂练习
1、一个圆柱的体积是30立方米,与它等底等高的圆锥的体积是( )立方米。
2、一个圆锥的体积是30立方米,与它等底等高的圆柱的体积是( )立方米。
10
90
V圆锥 = V圆柱× = 30× = 10m
V圆柱 = V圆锥×3 = 30×3 = 90m
填一填
1、圆锥的体积等于圆柱体积的三分之一。………( )
2、圆柱体的体积一定比圆锥体的体积大。………( )
3、一个圆锥与一个圆柱等底等高,已知圆锥
的体积是8立方米,圆柱的体积是24立方米。……( )
判断一下
×
×
√
题目没有说在等底等高的情况下
缺少必要数据:底面积和高
V圆柱 = V圆锥×3 =8×3=24m
解决问题
这两根冰淇淋的体积各是多少?哪根大呢?
1号
2号
底面积:
12.56cm2
高:
9cm
底面积:
28.26c㎡
高:
6cm
V = sh
= ×12.56×9
= 37.68cm
①号
V = sh
= ×28.26×6
= 56.52cm
②号
37.68cm < 56.52cm
答:1号冰淇淋的体积是37.68cm ,
2号冰淇淋的体积是56.52cm ,
所以2号冰淇淋大。
同学1
V = sh
= ×12.56×9
= ×9×12.56
= 3×12.56
= 37.68cm
V = sh
= ×28.26×6
= ×6×28.26
= 2×28.26
= 56.52cm
37.68cm < 56.52cm
答:1号冰淇淋的体积是37.68cm ,
2号是56.52cm ,2号大。
同学2
①
②
进行约分
解决问题
工地上有一堆沙子,近似于一个圆锥(如下图)。
这堆沙子的体积大约是多少?
V = sh
= ×[(4÷2) ×3.14]×1.2
= ×12.56×1.2
= ×1.2×12.56
= 5.024(m )
答:这堆沙子的体积大约是5.024m 。
同学1
V = sh
= ×3.14×2×1.2
= 3.14×0.8
= 28.26(m )
r = 4÷2=2(m)
答:这堆沙子的体积大约是2.826m 。
同学2
√
5.024(m )
r = 4÷2=2(m)
V = sh
= ×3.14×2×1.2
= 3.14×0.8
= 28.26(m )
s = πr
√
√
V = s h
没有乘平方
课堂小结
等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的三倍。
你有什么
收获吗?
等底等高的圆柱和圆锥,圆锥的体积是圆柱体积的 。
V圆锥 =
V圆柱
sh
=
圆锥的体积公式
只要你们多思、多想、多动,你们就可以自主探索出更多有趣的数学知识。
再 见!
