2023-2024学年初中数学人教版九年级下册27.2.1 相似三角形的判定 第3课时 课件(共20张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册27.2.1 相似三角形的判定 第3课时 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 587.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览


文档简介
(共20张PPT)
第二十七章 相似
27.2.1 相似三角形的判定
第3课时 利用两角相等判定
两三角形相似
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.探索两角分别相等的两个三角形相似的判定定理.
2.掌握利用两角来判定两个三角形相似的方法,并能进行
相关计算.
3. 掌握判定两个直角三角形相似的方法,并能进行相关计算.
合作探究
当堂检测
学习目标
课堂总结
自主学习
回顾:我们已经学了哪些两个三角形相似的判定方法?
合作探究
当堂检测
学习目标
课堂总结
自主学习
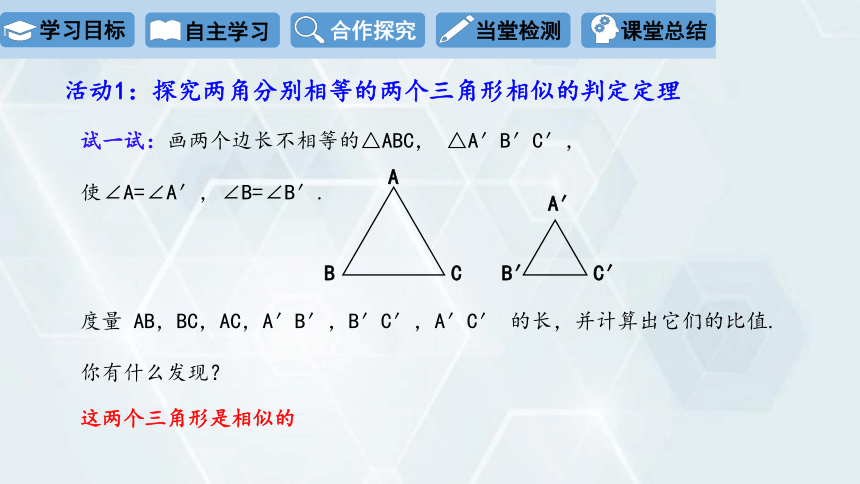
活动1:探究两角分别相等的两个三角形相似的判定定理
试一试:画两个边长不相等的△ABC, △A′B′C′,
使∠A=∠A′,∠B=∠B′.
A
A′
B
C
B′
C′
度量 AB,BC,AC,A′B′,B′C′,A′C′ 的长,并计算出它们的比值.
你有什么发现?
这两个三角形是相似的
合作探究
当堂检测
学习目标
课堂总结
自主学习
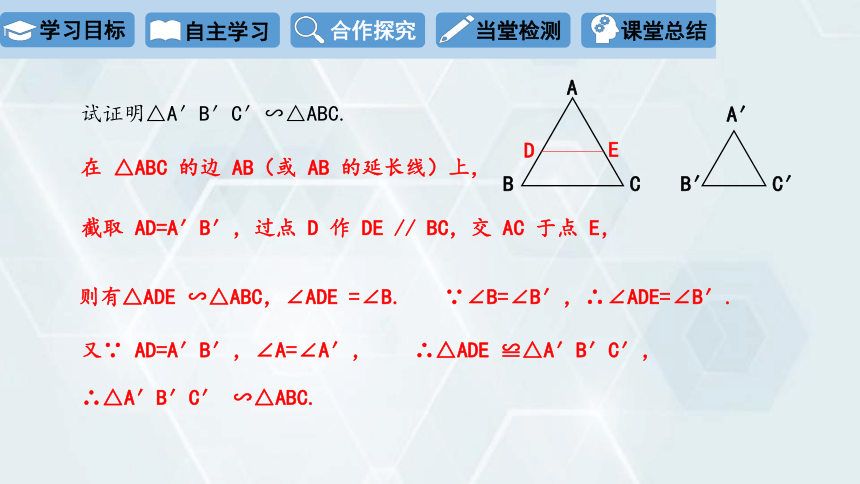
试证明△A′B′C′∽△ABC.
在 △ABC 的边 AB(或 AB 的延长线)上,
A
A′
B
C
B′
C′
∴△A′B′C′ ∽△ABC.
∴△ADE ≌△A′B′C′,
又∵ AD=A′B′,∠A=∠A′,
∵∠B=∠B′,∴∠ADE=∠B′.
则有△ADE ∽△ABC,∠ADE =∠B.
截取 AD=A′B′,过点 D 作 DE // BC,交 AC 于点 E,
D
E
合作探究
当堂检测
学习目标
课堂总结
自主学习
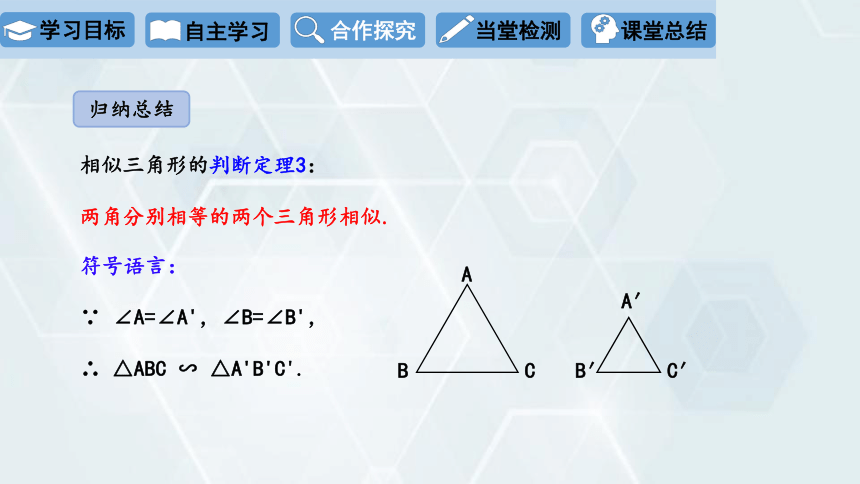
相似三角形的判断定理3:
两角分别相等的两个三角形相似.
符号语言:
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
A
A′
B
C
B′
C′
归纳总结
合作探究
当堂检测
学习目标
课堂总结
自主学习
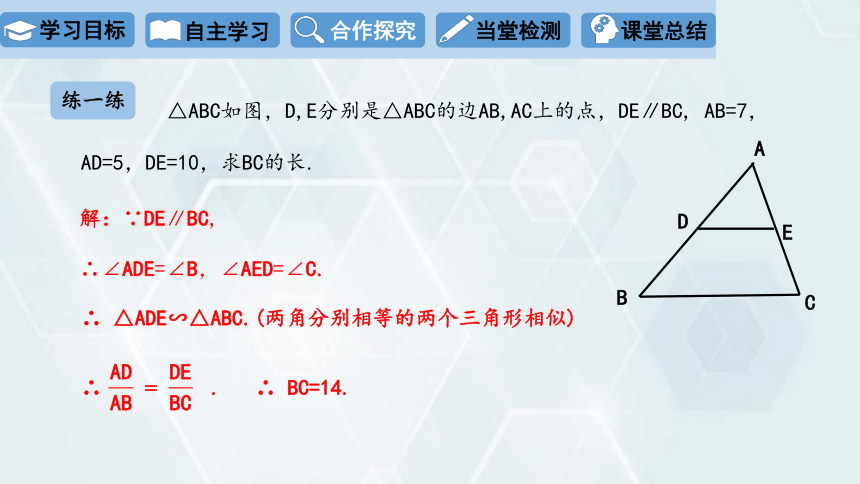
练一练
△ABC如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC, AB=7,
AD=5,DE=10,求BC的长.
解:∵DE∥BC,
∴ △ADE∽△ABC.(两角分别相等的两个三角形相似)
∴ .
∴∠ADE=∠B,∠AED=∠C.
B
A
D
E
C
∴ BC=14.
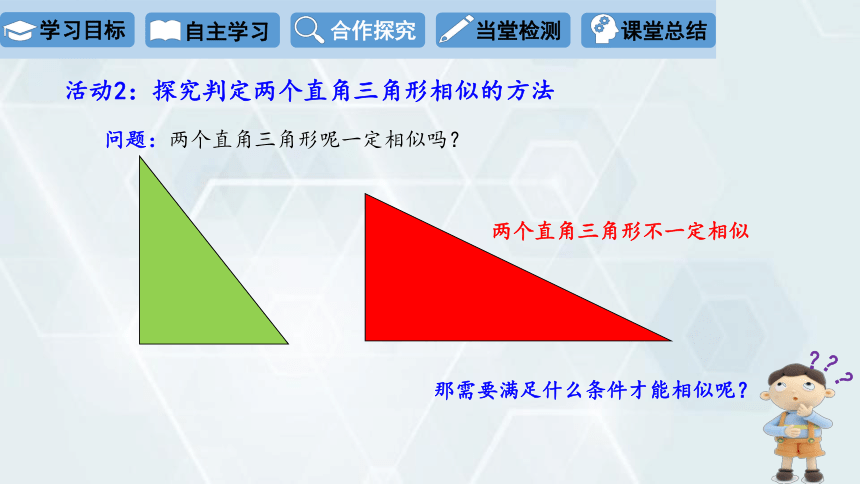
问题:两个直角三角形呢一定相似吗?
两个直角三角形不一定相似
那需要满足什么条件才能相似呢?
?
?
?
合作探究
当堂检测
学习目标
课堂总结
自主学习
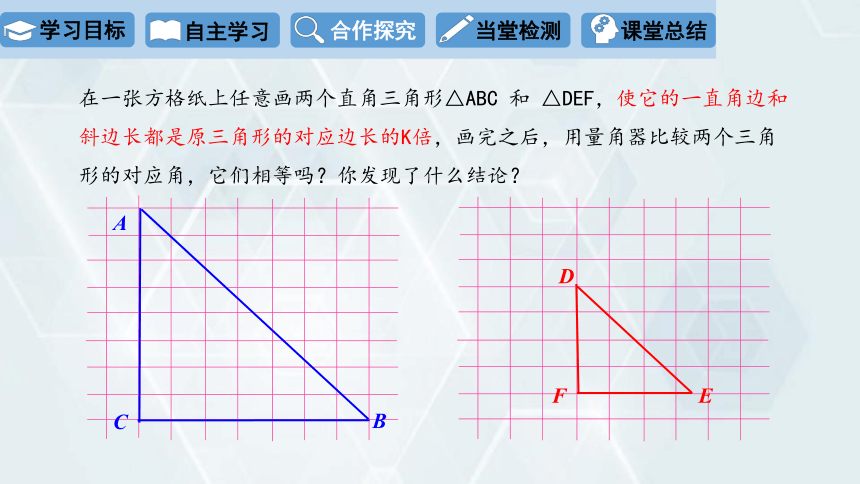
活动2:探究判定两个直角三角形相似的方法
在一张方格纸上任意画两个直角三角形△ABC 和 △DEF,使它的一直角边和斜边长都是原三角形的对应边长的K倍,画完之后,用量角器比较两个三角形的对应角,它们相等吗?你发现了什么结论?
E
F
D
C
B
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
我们发现:它们的三对角分别相等
即:∠A =∠D ,∠B =∠E,∠C=∠F
由定理1我们可知:两个角对应相等的两个三角形相似.
C
B
A
E
F
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
在Rt△ABC和 Rt△A′B′C′中∠C=C′=90°,
求证: Rt△ABC∽Rt△A′B′C′.
A
B
C
A'
B'
C'
证:设 则AB=kA'B',AC=kA'C'
根据勾股定理求得:B'C'= ,
BC=
∴Rt△ABC∽Rt△A'B'C'
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结
如果一个直角三角形的斜边和 一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
简记:斜边和一直角边对应成比例的两个直角三角形相似.
直角三角形相似的判定定理
符号语言:
∵∠B=∠B'=90°,
∴ △ABC ∽ △A'B'C'.
A
A'
B
C
B'
C'
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
C
在 Rt△ABC 和 Rt △DEF 中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
合作探究
当堂检测
学习目标
课堂总结
自主学习
判断直角三角形相似的方法:
① 有一锐角对应相等的两个直角三角形相似
② 有两组直角边对应成比例的两个直角三角形相似
③ 斜边和一直角边对应成比例的两个直角三角形相似
归纳总结
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.下列各组图形中可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如果一个直角三角形的两条边分别是 6 和 8,另一个与它相似的直角三角形边长分别是 3、4 及 x,那么x的值( )
A.10 B. C.5或 D.有无数个
C
注意:未明确对应关系,需要分类讨论.
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,
AB交于点D,E,连接BD.求证:△ABC∽△BDC.
证明:∵DE是AB的垂直平分线,∴AD=BD,
又∵∠C=∠C,∴△ABC∽△BDC.
∵∠ABC=80°,∴∠DBC=40°,∴∠DBC=∠BAC.
∴∠ABD=∠BAC=40°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
4.如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
解:∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°
设BP=x cm,则DP=(14-x)cm
∴①当 时,△ABP∽△CDP
解得x=8.4
②当 时,△ABP∽△PDC
解得x=2或12
综上所述:当BP=2cm或8.4cm或12cm时,△ABP和△CPD相似
6
4
14
x
14-x
即
即
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.相似三角形的判断定理3:
两角分别相等的两个三角形相似.
符号语言:
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
A
A′
B
C
B′
C′
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.直角三角形相似的判定定理:斜边和一直角边对应成比例的两个
直角三角形相似.
注意事项:(1)两个三角形必须都是直角三角形才能使用该定理;
(2)注意分清楚直角边的对应关系,若没有明确说明,则需要分类讨论;
(3)相似三角形的判定定理同样适用于直角三角形相似的判定.
第二十七章 相似
27.2.1 相似三角形的判定
第3课时 利用两角相等判定
两三角形相似
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.探索两角分别相等的两个三角形相似的判定定理.
2.掌握利用两角来判定两个三角形相似的方法,并能进行
相关计算.
3. 掌握判定两个直角三角形相似的方法,并能进行相关计算.
合作探究
当堂检测
学习目标
课堂总结
自主学习
回顾:我们已经学了哪些两个三角形相似的判定方法?
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1:探究两角分别相等的两个三角形相似的判定定理
试一试:画两个边长不相等的△ABC, △A′B′C′,
使∠A=∠A′,∠B=∠B′.
A
A′
B
C
B′
C′
度量 AB,BC,AC,A′B′,B′C′,A′C′ 的长,并计算出它们的比值.
你有什么发现?
这两个三角形是相似的
合作探究
当堂检测
学习目标
课堂总结
自主学习
试证明△A′B′C′∽△ABC.
在 △ABC 的边 AB(或 AB 的延长线)上,
A
A′
B
C
B′
C′
∴△A′B′C′ ∽△ABC.
∴△ADE ≌△A′B′C′,
又∵ AD=A′B′,∠A=∠A′,
∵∠B=∠B′,∴∠ADE=∠B′.
则有△ADE ∽△ABC,∠ADE =∠B.
截取 AD=A′B′,过点 D 作 DE // BC,交 AC 于点 E,
D
E
合作探究
当堂检测
学习目标
课堂总结
自主学习
相似三角形的判断定理3:
两角分别相等的两个三角形相似.
符号语言:
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
A
A′
B
C
B′
C′
归纳总结
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
△ABC如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC, AB=7,
AD=5,DE=10,求BC的长.
解:∵DE∥BC,
∴ △ADE∽△ABC.(两角分别相等的两个三角形相似)
∴ .
∴∠ADE=∠B,∠AED=∠C.
B
A
D
E
C
∴ BC=14.
问题:两个直角三角形呢一定相似吗?
两个直角三角形不一定相似
那需要满足什么条件才能相似呢?
?
?
?
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:探究判定两个直角三角形相似的方法
在一张方格纸上任意画两个直角三角形△ABC 和 △DEF,使它的一直角边和斜边长都是原三角形的对应边长的K倍,画完之后,用量角器比较两个三角形的对应角,它们相等吗?你发现了什么结论?
E
F
D
C
B
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
我们发现:它们的三对角分别相等
即:∠A =∠D ,∠B =∠E,∠C=∠F
由定理1我们可知:两个角对应相等的两个三角形相似.
C
B
A
E
F
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
在Rt△ABC和 Rt△A′B′C′中∠C=C′=90°,
求证: Rt△ABC∽Rt△A′B′C′.
A
B
C
A'
B'
C'
证:设 则AB=kA'B',AC=kA'C'
根据勾股定理求得:B'C'= ,
BC=
∴Rt△ABC∽Rt△A'B'C'
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结
如果一个直角三角形的斜边和 一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
简记:斜边和一直角边对应成比例的两个直角三角形相似.
直角三角形相似的判定定理
符号语言:
∵∠B=∠B'=90°,
∴ △ABC ∽ △A'B'C'.
A
A'
B
C
B'
C'
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
C
在 Rt△ABC 和 Rt △DEF 中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
合作探究
当堂检测
学习目标
课堂总结
自主学习
判断直角三角形相似的方法:
① 有一锐角对应相等的两个直角三角形相似
② 有两组直角边对应成比例的两个直角三角形相似
③ 斜边和一直角边对应成比例的两个直角三角形相似
归纳总结
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.下列各组图形中可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如果一个直角三角形的两条边分别是 6 和 8,另一个与它相似的直角三角形边长分别是 3、4 及 x,那么x的值( )
A.10 B. C.5或 D.有无数个
C
注意:未明确对应关系,需要分类讨论.
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,
AB交于点D,E,连接BD.求证:△ABC∽△BDC.
证明:∵DE是AB的垂直平分线,∴AD=BD,
又∵∠C=∠C,∴△ABC∽△BDC.
∵∠ABC=80°,∴∠DBC=40°,∴∠DBC=∠BAC.
∴∠ABD=∠BAC=40°.
合作探究
当堂检测
学习目标
课堂总结
自主学习
4.如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
解:∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°
设BP=x cm,则DP=(14-x)cm
∴①当 时,△ABP∽△CDP
解得x=8.4
②当 时,△ABP∽△PDC
解得x=2或12
综上所述:当BP=2cm或8.4cm或12cm时,△ABP和△CPD相似
6
4
14
x
14-x
即
即
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.相似三角形的判断定理3:
两角分别相等的两个三角形相似.
符号语言:
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
A
A′
B
C
B′
C′
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.直角三角形相似的判定定理:斜边和一直角边对应成比例的两个
直角三角形相似.
注意事项:(1)两个三角形必须都是直角三角形才能使用该定理;
(2)注意分清楚直角边的对应关系,若没有明确说明,则需要分类讨论;
(3)相似三角形的判定定理同样适用于直角三角形相似的判定.
