2023-2024学年初中数学人教版九年级下册27.2.2 相似三角形的性质 课件(共19张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册27.2.2 相似三角形的性质 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 399.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 08:40:39 | ||
图片预览






文档简介
(共19张PPT)
第二十七章 相似
27.2.2 相似三角形的性质
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. 理解并掌握相似三角形中对应线段的比等于相似比的性质,并能运用其解决问题.
2. 理解并掌握相似三角形面积的比等于相似比的平方的性质,并运用其解决问题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
C
B
A1
C1
B1
问题1:△ABC与△A1B1C1相似吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等.
高
角平分线
中线
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:如图,△ABC ∽△A'B'C',相似比为k,它们对应高的比是多少?
A
B
C
A'
B'
C'
D
D'
∵△ABC ∽△A'B'C',∴∠B=∠B',
解:分别作△ABC和△A'B'C'的高AD和A'D',
则∠ADB =∠A'D'B'=90°.
∴△ABD ∽△A'B'D' ,
合作探究
当堂检测
学习目标
课堂总结
自主学习
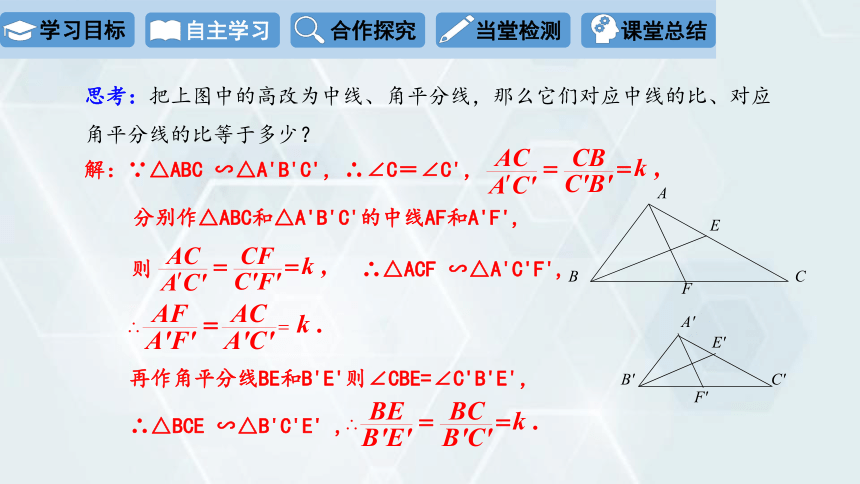
思考:把上图中的高改为中线、角平分线,那么它们对应中线的比、对应角平分线的比等于多少?
A'
B'
F'
C'
E'
A
B
C
F
E
再作角平分线BE和B'E'则∠CBE=∠C'B'E',
解:∵△ABC ∽△A'B'C',∴∠C=∠C',
∴△BCE ∽△B'C'E' ,
分别作△ABC和△A'B'C'的中线AF和A'F',
∴△ACF ∽△A'C'F',
则
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结
定理1:相似三角形对应高的比、对应角平分线的比、对应中线的比
都等于相似比.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:定理1的运用
两个相似三角形的对应边的高分别是6cm和8cm,如果它们对应的两条中线与两条角平分线的和为70cm,中线和与角平分线和为2:3,
问题提出:这两条对应中线的长分别是多少?
问题探究:(1)根据中线、角平分线的已知条件可得到什么?
中线和+角平分线和=70cm
中线和:角平分线和=2:3
解得:中线和=28cm
(2)相似三角形的对应高的比、对应中线的比有什么关系?
等于相似比
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:定理1的运用
两个相似三角形的对应边的高分别是6cm和8cm,如果它们对应的两条中线与两条角平分线的和为70cm,中线和与角平分线和为2:3.
问题解决:设较长的中线长为x cm,
∵中线和+角平分线和=70cm,中线和:角平分线和=2:3
∴中线和为28cm,
∴较短的中线长为(28-x)cm,
∵两个三角形相似,
解得:x=16,28-x=12,
答:这两条对应中线长分别为12cm、16cm.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
6
1.ΔABC∽ΔA1B1C1 ,BD和B1D1是它们的中线,已知AC是A1C1的1.5倍,
B1D1 =4cm,则BD= cm.
2.ΔABC∽ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=2cm ,则ΔABC与ΔA1B1C1的对应高之比为 .
4
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题3:如图,△ABC ∽△A'B'C',相似比为k,
(1)C△ABC:C△A'B'C'= ,
理由: ;
(2)S△ABC:S△A'B'C'= ,
理由: .
A
B
C
A'
B'
C'
k
比例的等比性质
k2
可写成:对应高的比·对应边的比=k·k=k2
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结
定理2:相似三角形的周长比等于相似比,
面积比等于相似比的平方.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:定理2的运用
问题提出:如图,D,E分别是AC,AB上的点,已知△ABC的面积为100cm2,且 ,求四边形BCDE的面积.
问题探究:(1)△ADE与△ABC有什么关系?
相似,且相似比为0.6
(2)S△ADE与S△ABC的数量关系是什么?
B
C
A
D
E
S△ADE=0.36S△ABC
(3)S四边形BCDE与S△ABC的数量关系是什么?
S四边形BCDE=0.64S△ABC
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:定理2的运用
问题提出:如图,D,E分别是AC,AB上的点,已知△ABC的面积为100cm2,且 ,求四边形BCDE的面积.
∴△ADE∽△ABC,且相似比k=0.6,
B
C
A
D
E
问题解决:∵∠A=∠A,且
∴S△ADE = 0.36S△ABC ,
∴S四边形BCDE =S△ABC -S△ADE =0.64S△ABC =64(cm2),
答:四边形BCDE的面积为64cm2.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
3.如图,△ABC中,点D、E、F分别在AB、AC、BC上,且DE∥BC,EF∥AB. 当D点为AB中点时,求S△ABC : S四边形BFED的值.
A
B
C
D
F
E
解:∵ DE∥BC,D为AB中点,
∴△ADE∽△ABC,且相似比为1:2,E为AC中点,
∴S△ADE:S△ABC=1:4,
同理:S△CEF:S△CAB=1:4 ,
设S△ABC=4a,则S△ADE = S△CEF =a,
∴S四边形BFED=S△ABC-S△ADE-S△CEF =2a,
∴S△ABC : S四边形BFED= 0.5 .
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. 判断:
(1)一个三角形的各边长缩小为原来的2倍,这个三角形的高也缩小为原来的2倍 ( )
(2)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍 ( )
(3)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍 ( )
√
×
√
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
1.5
P
A
D
B
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为 4 和 9,求△ABC的面积.
A
B
C
D
F
E
解:∵ DE∥BC,EF∥AB,
∴ △ADE ∽△ABC,∠ADE =∠EFC,∠A =∠CEF,
∴△ADE ∽△EFC.
又∵S△ADE : S△EFC = 4 : 9,
∴AE : EC=2:3,
∴ S△ADE : S△ABC = 4 : 25,
则 AE : AC =2 : 5,
∴ S△ABC = 25.
合作探究
当堂检测
学习目标
课堂总结
自主学习
相似三角形的性质
(1)相似三角形的对应角相等,对应边成比例;
(2)相似三角形对应高的比、对应中线的比与对应角平分线的比等于相似比;
(3)相似三角形的周长比等于相似比;
(4)相似三角形的面积比等于相似比的平方.
第二十七章 相似
27.2.2 相似三角形的性质
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. 理解并掌握相似三角形中对应线段的比等于相似比的性质,并能运用其解决问题.
2. 理解并掌握相似三角形面积的比等于相似比的平方的性质,并运用其解决问题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
C
B
A1
C1
B1
问题1:△ABC与△A1B1C1相似吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等.
高
角平分线
中线
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:如图,△ABC ∽△A'B'C',相似比为k,它们对应高的比是多少?
A
B
C
A'
B'
C'
D
D'
∵△ABC ∽△A'B'C',∴∠B=∠B',
解:分别作△ABC和△A'B'C'的高AD和A'D',
则∠ADB =∠A'D'B'=90°.
∴△ABD ∽△A'B'D' ,
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:把上图中的高改为中线、角平分线,那么它们对应中线的比、对应角平分线的比等于多少?
A'
B'
F'
C'
E'
A
B
C
F
E
再作角平分线BE和B'E'则∠CBE=∠C'B'E',
解:∵△ABC ∽△A'B'C',∴∠C=∠C',
∴△BCE ∽△B'C'E' ,
分别作△ABC和△A'B'C'的中线AF和A'F',
∴△ACF ∽△A'C'F',
则
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结
定理1:相似三角形对应高的比、对应角平分线的比、对应中线的比
都等于相似比.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:定理1的运用
两个相似三角形的对应边的高分别是6cm和8cm,如果它们对应的两条中线与两条角平分线的和为70cm,中线和与角平分线和为2:3,
问题提出:这两条对应中线的长分别是多少?
问题探究:(1)根据中线、角平分线的已知条件可得到什么?
中线和+角平分线和=70cm
中线和:角平分线和=2:3
解得:中线和=28cm
(2)相似三角形的对应高的比、对应中线的比有什么关系?
等于相似比
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:定理1的运用
两个相似三角形的对应边的高分别是6cm和8cm,如果它们对应的两条中线与两条角平分线的和为70cm,中线和与角平分线和为2:3.
问题解决:设较长的中线长为x cm,
∵中线和+角平分线和=70cm,中线和:角平分线和=2:3
∴中线和为28cm,
∴较短的中线长为(28-x)cm,
∵两个三角形相似,
解得:x=16,28-x=12,
答:这两条对应中线长分别为12cm、16cm.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
6
1.ΔABC∽ΔA1B1C1 ,BD和B1D1是它们的中线,已知AC是A1C1的1.5倍,
B1D1 =4cm,则BD= cm.
2.ΔABC∽ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=2cm ,则ΔABC与ΔA1B1C1的对应高之比为 .
4
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题3:如图,△ABC ∽△A'B'C',相似比为k,
(1)C△ABC:C△A'B'C'= ,
理由: ;
(2)S△ABC:S△A'B'C'= ,
理由: .
A
B
C
A'
B'
C'
k
比例的等比性质
k2
可写成:对应高的比·对应边的比=k·k=k2
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结
定理2:相似三角形的周长比等于相似比,
面积比等于相似比的平方.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:定理2的运用
问题提出:如图,D,E分别是AC,AB上的点,已知△ABC的面积为100cm2,且 ,求四边形BCDE的面积.
问题探究:(1)△ADE与△ABC有什么关系?
相似,且相似比为0.6
(2)S△ADE与S△ABC的数量关系是什么?
B
C
A
D
E
S△ADE=0.36S△ABC
(3)S四边形BCDE与S△ABC的数量关系是什么?
S四边形BCDE=0.64S△ABC
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:定理2的运用
问题提出:如图,D,E分别是AC,AB上的点,已知△ABC的面积为100cm2,且 ,求四边形BCDE的面积.
∴△ADE∽△ABC,且相似比k=0.6,
B
C
A
D
E
问题解决:∵∠A=∠A,且
∴S△ADE = 0.36S△ABC ,
∴S四边形BCDE =S△ABC -S△ADE =0.64S△ABC =64(cm2),
答:四边形BCDE的面积为64cm2.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
3.如图,△ABC中,点D、E、F分别在AB、AC、BC上,且DE∥BC,EF∥AB. 当D点为AB中点时,求S△ABC : S四边形BFED的值.
A
B
C
D
F
E
解:∵ DE∥BC,D为AB中点,
∴△ADE∽△ABC,且相似比为1:2,E为AC中点,
∴S△ADE:S△ABC=1:4,
同理:S△CEF:S△CAB=1:4 ,
设S△ABC=4a,则S△ADE = S△CEF =a,
∴S四边形BFED=S△ABC-S△ADE-S△CEF =2a,
∴S△ABC : S四边形BFED= 0.5 .
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. 判断:
(1)一个三角形的各边长缩小为原来的2倍,这个三角形的高也缩小为原来的2倍 ( )
(2)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍 ( )
(3)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍 ( )
√
×
√
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
1.5
P
A
D
B
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为 4 和 9,求△ABC的面积.
A
B
C
D
F
E
解:∵ DE∥BC,EF∥AB,
∴ △ADE ∽△ABC,∠ADE =∠EFC,∠A =∠CEF,
∴△ADE ∽△EFC.
又∵S△ADE : S△EFC = 4 : 9,
∴AE : EC=2:3,
∴ S△ADE : S△ABC = 4 : 25,
则 AE : AC =2 : 5,
∴ S△ABC = 25.
合作探究
当堂检测
学习目标
课堂总结
自主学习
相似三角形的性质
(1)相似三角形的对应角相等,对应边成比例;
(2)相似三角形对应高的比、对应中线的比与对应角平分线的比等于相似比;
(3)相似三角形的周长比等于相似比;
(4)相似三角形的面积比等于相似比的平方.
