2023-2024学年初中数学人教版九年级下册27.2.3 相似三角形应用举例 课件(共21张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册27.2.3 相似三角形应用举例 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第二十七章 相似
27.2.3 相似三角形的应用举例
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解并掌握运用相似三角形测量物体高度的方法.
2.理解并掌握运用相似三角形测量物体宽度的方法.
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:世界上有许多高山,有许多大河,在我们无法到达其顶端,
无法跨越到对岸时,如何才能知道“山有多高,河有多宽”呢
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1:利用影长测量物体的高度
你们有过测量物体高度的体验吗?你有什么方法测量金字塔的高度?
合作探究
当堂检测
学习目标
课堂总结
自主学习
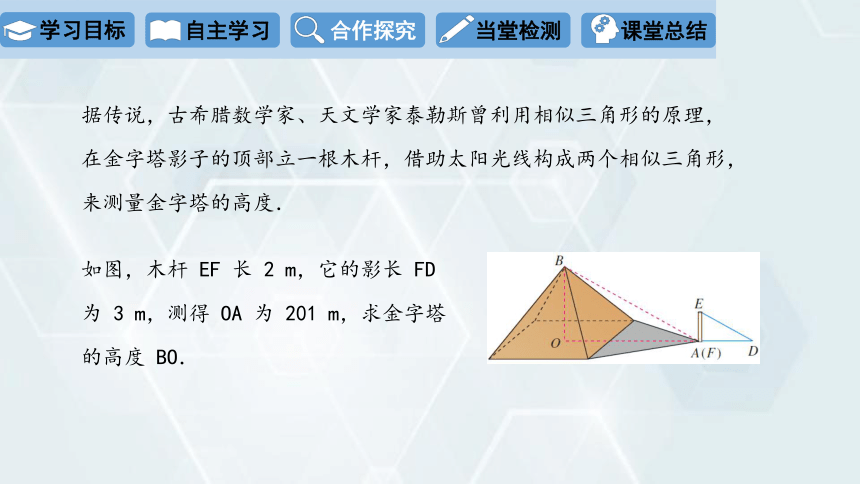
据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,
在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,
来测量金字塔的高度.
如图,木杆 EF 长 2 m,它的影长 FD
为 3 m,测得 OA 为 201 m,求金字塔
的高度 BO.
合作探究
当堂检测
学习目标
课堂总结
自主学习
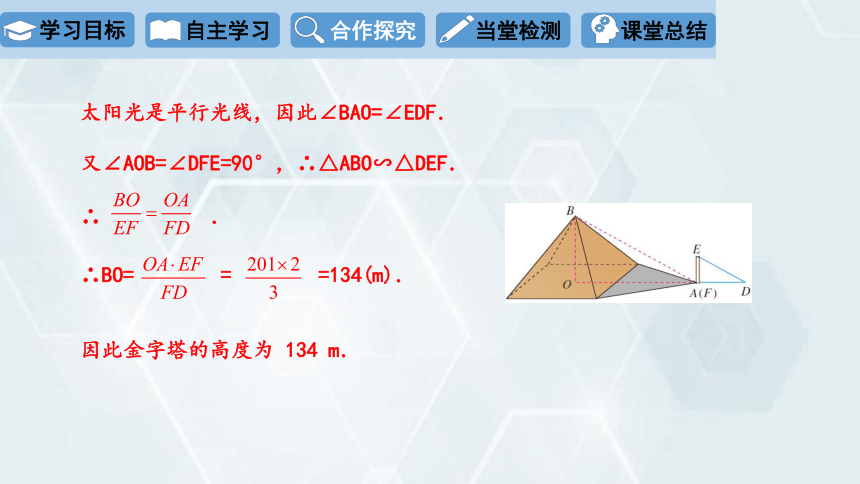
太阳光是平行光线,因此∠BAO=∠EDF.
又∠AOB=∠DFE=90°,∴△ABO∽△DEF.
∴ .
∴BO= = =134(m).
因此金字塔的高度为 134 m.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:1.测量原理:测量不能直接到达顶部的物体的高度,一般利用
“相似三角形对应边成比例”和“在同一时刻太阳光下物体的高度与影长
成比例”的原理解决.
2.测量方法:在同一时刻量出太阳光下参照物和被测物体的影长,再根据
参照物的高度计算出被测物体的高度.
注意:运用此测量方法时,要符合下列两个条件:
(1)被测物体的底部能够到达;
(2)由于影子长可能随着大阳的运动而变化,因此要在同一时刻测量参照物
与被测物体的影长.
合作探究
当堂检测
学习目标
课堂总结
自主学习
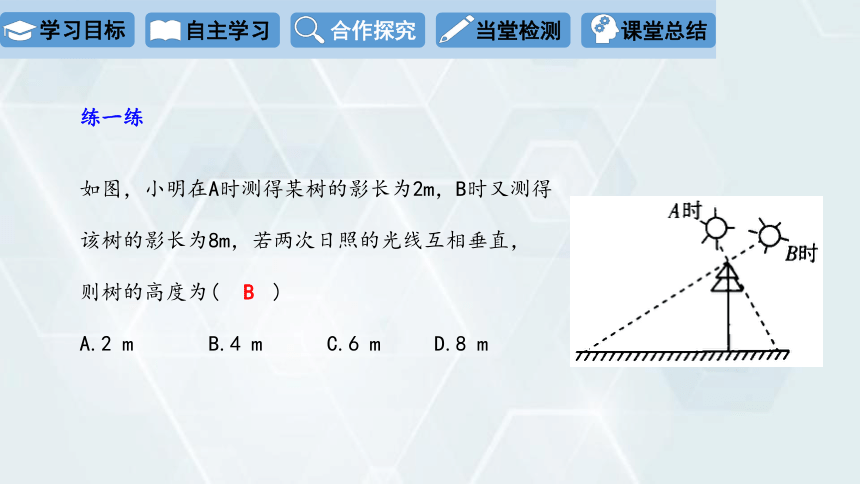
练一练
如图,小明在A时测得某树的影长为2m,B时又测得
该树的影长为8m,若两次日照的光线互相垂直,
则树的高度为( )
A.2 m B.4 m C.6 m D.8 m
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:利用镜子的反射测量物体的高度
如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.在点P处水平
放一平面镜,光线从点A发出经平面镜反射后刚好照到古城墙CD的顶端C处,
已知AB⊥BD,CD⊥BD,
测得AB=2米,BP=3米,PD=12米,
求该古城墙CD的高度.
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:如图,由题意可得∠APE=∠CPE,∴∠APB=∠CPD,
故该古城墙CD的高度为8米.
∴ ,∴CD=8米,
∵AB=2米,BP=3米,PD=12米,
∴ ,
∴△ABP∽△CDP,
∴∠ABP=∠CDP=90°,
∵AB⊥BD,CD⊥BD,
E
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:1.测量原理:利用镜子的反射,先根据入射角等于反射角的原理
构造相似三角形,再计算所求物体的高度.
2.测量方法:
(1)在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记;
(2)测出观测者眼睛到地面的高度;
(3)观测者看着镜子来回走动,直至看到旗杆顶端在镜子中的像与镜子上的标记
重合,此时测出镜子上的标记位置到观测者脚底的距离及到旗杆底端的距离;
(4)根据两角分别相等推导出两个三角形相似,利用对应边成比例求出旗杆的
高度注意测量时被测物体与人之间不能有障碍物,且镜子要水平放置.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
小丽同学测量操场上旗杆的高度,她先将镜子放在脚下的地面上,
然后后退,直A到她站直身子刚好能从镜子里看到旗杆的顶端E,
标记好脚掌中心位置为B.测得脚掌中心位置B到镜面中心C的距离
是50cm,镜面中心C距旗杆底部D的距离为4m,如图所示已知小丽
同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,
则旗杆DE的高度等于( )
A.10m B.12m C.12.4m D.12.32m
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动3:利用相似测量河宽
在无法过河的条件下,怎样估算河的宽度?
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在近岸取
点 Q 和 S,使点 P,Q,S 共线且直线 PS 与河垂直,接着在过点 S 且与 PS
垂直的直线 a 上选择适当的点 T,
确定 PT 与过点Q 且垂直 PS 的
直线 b 的交点 R.已测得 QS = 45 m,
ST = 90 m,QR = 60 m,
请根据这些数据,计算河宽 PQ.
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:∵∠PQR=∠PST=90°,∠P=∠P,∴△PQR∽△PST.
PQ×90=(PQ+45)×60.
解得 PQ=90(m).因此,河宽大约为 90m.
∴ .
即 , .
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:1.测量原理:测量不能直接到达的两点间的距离,常常构造“X”
型或“A”型的相似三角形,利用相似三角形的性质计算两点间的距离.
2.测量方法:
(1)如图,分别测量出BC,CD和ED的
长度,利用△ABC∽△EDC,得 ,即 ,从而可求得河流的宽度.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2)如图,可以分别测量出BD,AB和
ED的长度,利用△ABC∽△EDC,
得 ,
即 ,
从而可求得河流的宽度.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,小明在打网球时,使球恰好能打过网,并且落在离网4米的位置上,
则球拍击球的高度h为( )
A.1.6米 B.1.5米
C.2.4米 D.1.2米
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,A,B两地之间有一个池塘,要测量A,B两地之间的距离,选择一点O,
连接AO并延长到点C,使OC=0.5AO,连接BO并延长到点D,使OD=0.5BO.
测得C,D间距离为30米,则A,B两地之间的距离为( )
A.30米 B.45米
C.60米 D.90米
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整
自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知
纸板的两条边DF=50 cm, EF=30 cm,测得边DF离地面的高度AC=1.5 m,
CD=20 m,则树高AB为 ( )
A.12 m B.13.5 m
C.15 m D.16.5 m
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.相似三角形的应用
(1)测高 (不能直接使用皮尺或刻度尺量的高度);
(2)测距 (不能直接测量的两点间的距离).
2.测高的方法
测量不能到达顶部的物体的高度,构造相似三角形求解.
3.测距的方法
测量不能到达两点间的距离,常构造相似三角形求解.
第二十七章 相似
27.2.3 相似三角形的应用举例
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解并掌握运用相似三角形测量物体高度的方法.
2.理解并掌握运用相似三角形测量物体宽度的方法.
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:世界上有许多高山,有许多大河,在我们无法到达其顶端,
无法跨越到对岸时,如何才能知道“山有多高,河有多宽”呢
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1:利用影长测量物体的高度
你们有过测量物体高度的体验吗?你有什么方法测量金字塔的高度?
合作探究
当堂检测
学习目标
课堂总结
自主学习
据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,
在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,
来测量金字塔的高度.
如图,木杆 EF 长 2 m,它的影长 FD
为 3 m,测得 OA 为 201 m,求金字塔
的高度 BO.
合作探究
当堂检测
学习目标
课堂总结
自主学习
太阳光是平行光线,因此∠BAO=∠EDF.
又∠AOB=∠DFE=90°,∴△ABO∽△DEF.
∴ .
∴BO= = =134(m).
因此金字塔的高度为 134 m.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:1.测量原理:测量不能直接到达顶部的物体的高度,一般利用
“相似三角形对应边成比例”和“在同一时刻太阳光下物体的高度与影长
成比例”的原理解决.
2.测量方法:在同一时刻量出太阳光下参照物和被测物体的影长,再根据
参照物的高度计算出被测物体的高度.
注意:运用此测量方法时,要符合下列两个条件:
(1)被测物体的底部能够到达;
(2)由于影子长可能随着大阳的运动而变化,因此要在同一时刻测量参照物
与被测物体的影长.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,小明在A时测得某树的影长为2m,B时又测得
该树的影长为8m,若两次日照的光线互相垂直,
则树的高度为( )
A.2 m B.4 m C.6 m D.8 m
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:利用镜子的反射测量物体的高度
如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.在点P处水平
放一平面镜,光线从点A发出经平面镜反射后刚好照到古城墙CD的顶端C处,
已知AB⊥BD,CD⊥BD,
测得AB=2米,BP=3米,PD=12米,
求该古城墙CD的高度.
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:如图,由题意可得∠APE=∠CPE,∴∠APB=∠CPD,
故该古城墙CD的高度为8米.
∴ ,∴CD=8米,
∵AB=2米,BP=3米,PD=12米,
∴ ,
∴△ABP∽△CDP,
∴∠ABP=∠CDP=90°,
∵AB⊥BD,CD⊥BD,
E
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:1.测量原理:利用镜子的反射,先根据入射角等于反射角的原理
构造相似三角形,再计算所求物体的高度.
2.测量方法:
(1)在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记;
(2)测出观测者眼睛到地面的高度;
(3)观测者看着镜子来回走动,直至看到旗杆顶端在镜子中的像与镜子上的标记
重合,此时测出镜子上的标记位置到观测者脚底的距离及到旗杆底端的距离;
(4)根据两角分别相等推导出两个三角形相似,利用对应边成比例求出旗杆的
高度注意测量时被测物体与人之间不能有障碍物,且镜子要水平放置.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
小丽同学测量操场上旗杆的高度,她先将镜子放在脚下的地面上,
然后后退,直A到她站直身子刚好能从镜子里看到旗杆的顶端E,
标记好脚掌中心位置为B.测得脚掌中心位置B到镜面中心C的距离
是50cm,镜面中心C距旗杆底部D的距离为4m,如图所示已知小丽
同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,
则旗杆DE的高度等于( )
A.10m B.12m C.12.4m D.12.32m
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动3:利用相似测量河宽
在无法过河的条件下,怎样估算河的宽度?
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在近岸取
点 Q 和 S,使点 P,Q,S 共线且直线 PS 与河垂直,接着在过点 S 且与 PS
垂直的直线 a 上选择适当的点 T,
确定 PT 与过点Q 且垂直 PS 的
直线 b 的交点 R.已测得 QS = 45 m,
ST = 90 m,QR = 60 m,
请根据这些数据,计算河宽 PQ.
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:∵∠PQR=∠PST=90°,∠P=∠P,∴△PQR∽△PST.
PQ×90=(PQ+45)×60.
解得 PQ=90(m).因此,河宽大约为 90m.
∴ .
即 , .
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:1.测量原理:测量不能直接到达的两点间的距离,常常构造“X”
型或“A”型的相似三角形,利用相似三角形的性质计算两点间的距离.
2.测量方法:
(1)如图,分别测量出BC,CD和ED的
长度,利用△ABC∽△EDC,得 ,即 ,从而可求得河流的宽度.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2)如图,可以分别测量出BD,AB和
ED的长度,利用△ABC∽△EDC,
得 ,
即 ,
从而可求得河流的宽度.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,小明在打网球时,使球恰好能打过网,并且落在离网4米的位置上,
则球拍击球的高度h为( )
A.1.6米 B.1.5米
C.2.4米 D.1.2米
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,A,B两地之间有一个池塘,要测量A,B两地之间的距离,选择一点O,
连接AO并延长到点C,使OC=0.5AO,连接BO并延长到点D,使OD=0.5BO.
测得C,D间距离为30米,则A,B两地之间的距离为( )
A.30米 B.45米
C.60米 D.90米
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整
自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知
纸板的两条边DF=50 cm, EF=30 cm,测得边DF离地面的高度AC=1.5 m,
CD=20 m,则树高AB为 ( )
A.12 m B.13.5 m
C.15 m D.16.5 m
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.相似三角形的应用
(1)测高 (不能直接使用皮尺或刻度尺量的高度);
(2)测距 (不能直接测量的两点间的距离).
2.测高的方法
测量不能到达顶部的物体的高度,构造相似三角形求解.
3.测距的方法
测量不能到达两点间的距离,常构造相似三角形求解.
