2023-2024学年初中数学人教版九年级下册27.3 位似 第1课时 课件(共23张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册27.3 位似 第1课时 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 530.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
第二十七章 相似
27.3 位似
第1课时 位似图形的概念及画法
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. 掌握位似图形的概念、性质和画法.
2. 掌握位似与相似的联系与区别.
合作探究
当堂检测
学习目标
课堂总结
自主学习
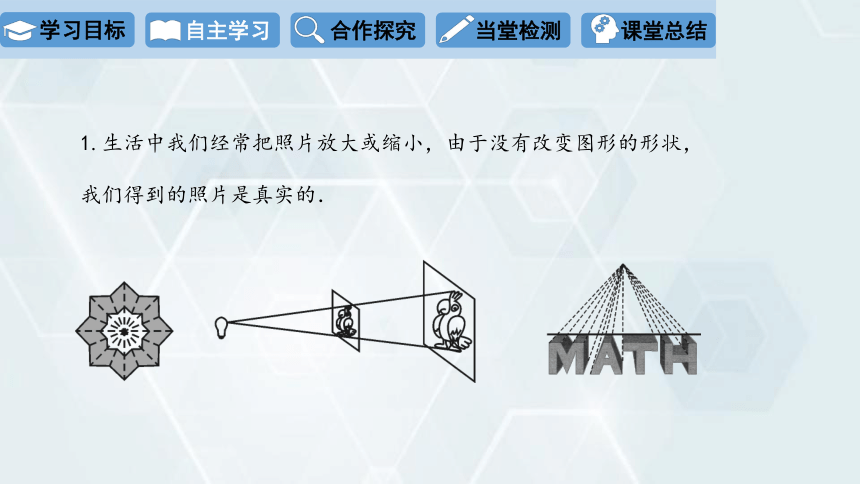
1.生活中我们经常把照片放大或缩小,由于没有改变图形的形状,
我们得到的照片是真实的.
合作探究
当堂检测
学习目标
课堂总结
自主学习
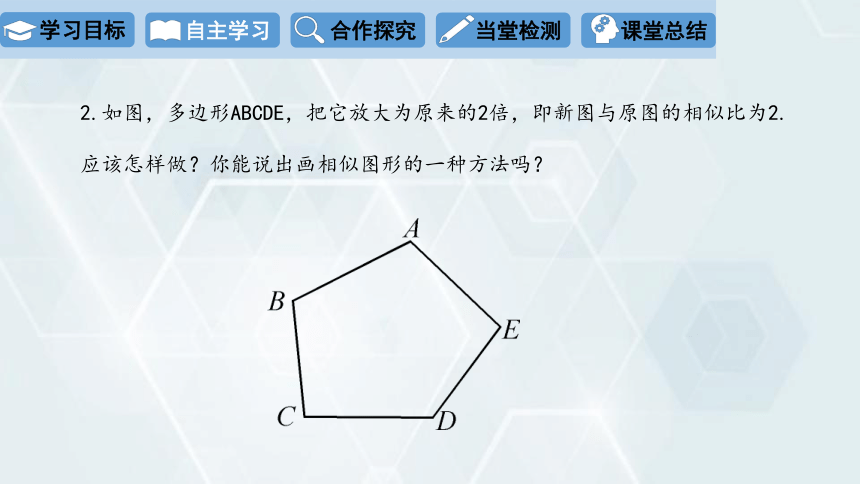
2.如图,多边形ABCDE,把它放大为原来的2倍,即新图与原图的相似比为2.
应该怎样做?你能说出画相似图形的一种方法吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
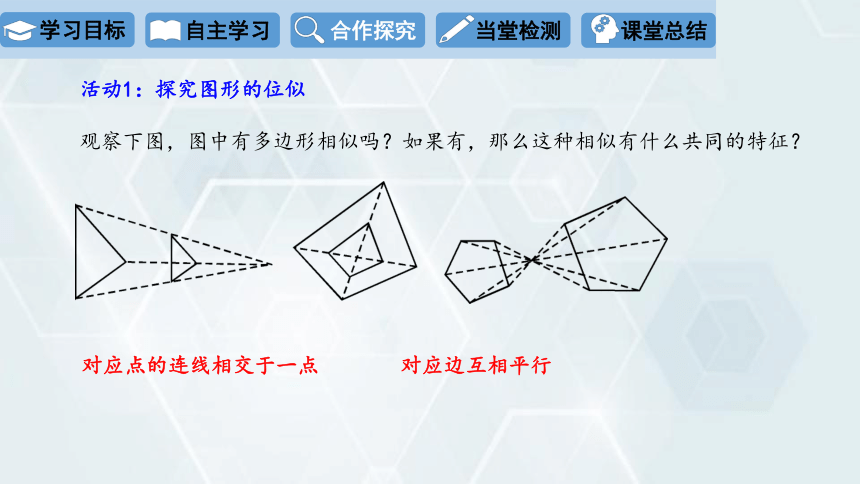
活动1:探究图形的位似
观察下图,图中有多边形相似吗?如果有,那么这种相似有什么共同的特征?
对应点的连线相交于一点
对应边互相平行
合作探究
当堂检测
学习目标
课堂总结
自主学习
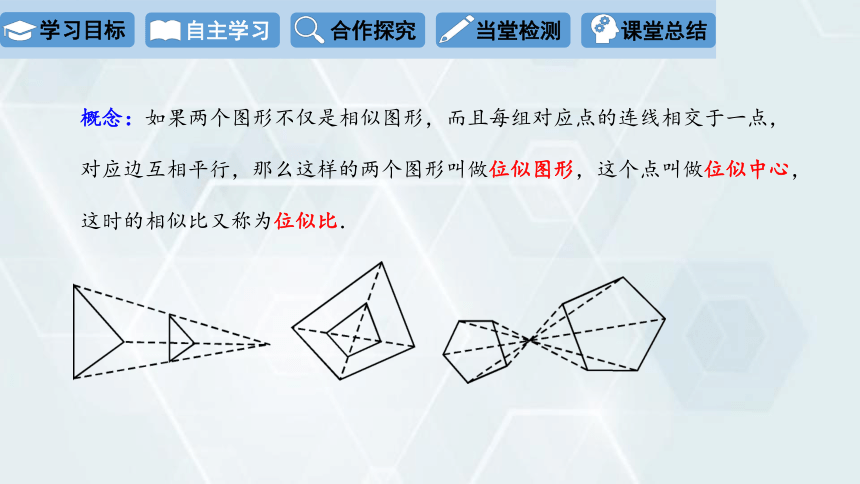
概念:如果两个图形不仅是相似图形,而且每组对应点的连线相交于一点,
对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心,
这时的相似比又称为位似比.
合作探究
当堂检测
学习目标
课堂总结
自主学习
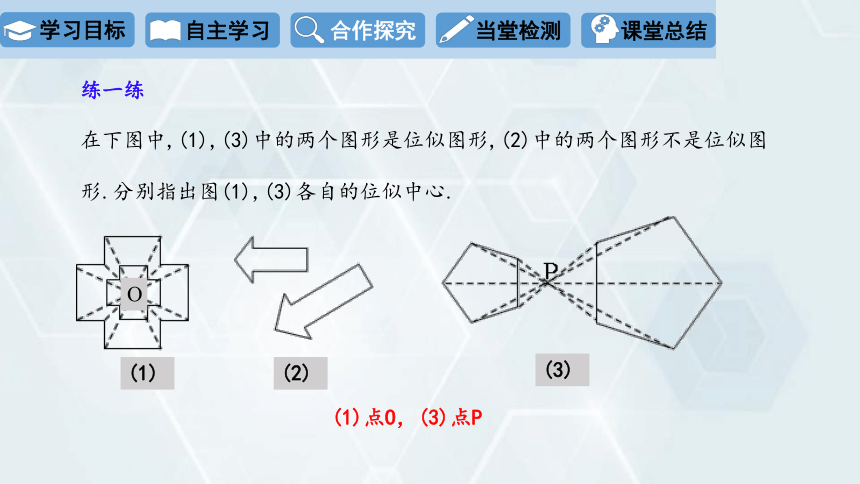
练一练
在下图中,(1),(3)中的两个图形是位似图形,(2)中的两个图形不是位似图形.分别指出图(1),(3)各自的位似中心.
(1)
(2)
(3)
O
(1)点O,(3)点P
合作探究
当堂检测
学习目标
课堂总结
自主学习
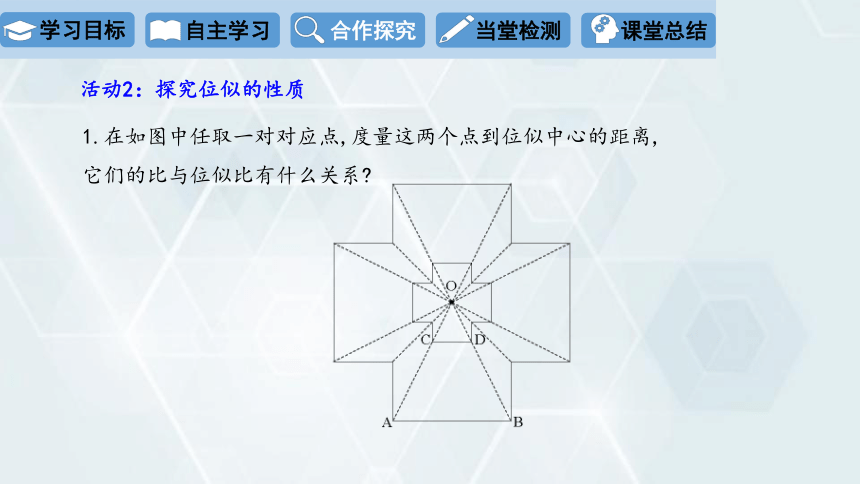
1.在如图中任取一对对应点,度量这两个点到位似中心的距离,
它们的比与位似比有什么关系
活动2:探究位似的性质
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.在下图中再试一试,还有类似的规律吗 位似图形还有哪些性质?
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:位似图形的性质:
1.位似图形是一种特殊的相似图形,它具有相似图形的所有性质,
即对应角相等,对应边的比相等.
2.位似图形上任意一对对应点到位似中心的距离之比等于相似比.
(位似图形的相似比也叫做位似比)
3.位似图形对应点和位似中心在同一条直线上
4.对应线段平行或者在一条直线上.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动3:位似的画法
把图中的四边形ABCD缩小到原来的 .
提示:使新图形上各顶点到位似中心的距离与原图形各对应顶点到
位似中心的距离之比为1∶2.
合作探究
当堂检测
学习目标
课堂总结
自主学习
作法1:
(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′,B′,C′,D′,
使得 ;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,所得四边形A′B′C′D′
就是所要求作的图形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
作法2:
(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD反向延长线上取点A′,B′,C′,D′,
使得 ;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,所得四边形A′B′C′D′
就是所要求作的图形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
作法3:
(1)在四边形ABCD内任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′,B′,C′,D′,
使得 ;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,所得四边形A′B′C′D′
就是所要求作的图形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:作位似图形的基本步骤:
(1)确定位似中心;
(2)连接图形各顶点与位似中心;
(3)在连接图形各顶点与位似中心的直线上按相似比进行取点;
(4)顺次连接各点,所得图形就是所求的图形;
(5)有时符合条件的位似图形不止一个,有时需要根据题意进行取舍.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.在下列图形中,不是位似图形的是( )
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,点F在BD上,BC,AD相交于点E,且AB∥CD∥EF.图中的位似三角形
有 , , .
△DFE与△DBA
△BFE与△BDC
△AEB与△DEC
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.点A,B,C,D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB
成位似图形,则位似中心为( )
A.点E B.点F
C.点H D.点G
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
4.如图,△ABC与△DEF是位似图形,相似比是1∶2,已知DE=4,则AB的长
是( )
A.2 B.4
C.8 D.1
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
5.如图是△ABC位似图形的几种画法,其中正确的个数是( )
A.1 B.2 C.3 D.4
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
6.已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,
且位似比为1:2.
A
B
C
D
E
F
解:画射线OA,OB,OC;
在射线OA,OB,OC上分别取点D,E,F,
使OA = 2OD,OB = 2OE,OC = 2OF;
顺序连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
0
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.位似图形的概念
如果两个图形不仅是相似图形,而且每组对应点的连线相交于一点,
对应边互相平行,那么这样的两个图形叫做位似图形.
2.位似图形的性质
(1)位似图形一定相似,位似比等于相似比;
(2)位似图形对应点和位似中心在同一条直线上;
(3)任意一对对应点到位似中心的距离之比等于位似比或相似比;
(4)对应线段平行或者在一条直线上.
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.位似图形的画法
(1)确定位似中心;
(2)连接图形各顶点与位似中心;
(3)在连接图形各顶点与位似中心的直线上按相似比进行取点;
(4)顺次连接各点,所得图形就是所求的图形.
第二十七章 相似
27.3 位似
第1课时 位似图形的概念及画法
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. 掌握位似图形的概念、性质和画法.
2. 掌握位似与相似的联系与区别.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.生活中我们经常把照片放大或缩小,由于没有改变图形的形状,
我们得到的照片是真实的.
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,多边形ABCDE,把它放大为原来的2倍,即新图与原图的相似比为2.
应该怎样做?你能说出画相似图形的一种方法吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1:探究图形的位似
观察下图,图中有多边形相似吗?如果有,那么这种相似有什么共同的特征?
对应点的连线相交于一点
对应边互相平行
合作探究
当堂检测
学习目标
课堂总结
自主学习
概念:如果两个图形不仅是相似图形,而且每组对应点的连线相交于一点,
对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心,
这时的相似比又称为位似比.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
在下图中,(1),(3)中的两个图形是位似图形,(2)中的两个图形不是位似图形.分别指出图(1),(3)各自的位似中心.
(1)
(2)
(3)
O
(1)点O,(3)点P
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.在如图中任取一对对应点,度量这两个点到位似中心的距离,
它们的比与位似比有什么关系
活动2:探究位似的性质
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.在下图中再试一试,还有类似的规律吗 位似图形还有哪些性质?
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:位似图形的性质:
1.位似图形是一种特殊的相似图形,它具有相似图形的所有性质,
即对应角相等,对应边的比相等.
2.位似图形上任意一对对应点到位似中心的距离之比等于相似比.
(位似图形的相似比也叫做位似比)
3.位似图形对应点和位似中心在同一条直线上
4.对应线段平行或者在一条直线上.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动3:位似的画法
把图中的四边形ABCD缩小到原来的 .
提示:使新图形上各顶点到位似中心的距离与原图形各对应顶点到
位似中心的距离之比为1∶2.
合作探究
当堂检测
学习目标
课堂总结
自主学习
作法1:
(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′,B′,C′,D′,
使得 ;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,所得四边形A′B′C′D′
就是所要求作的图形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
作法2:
(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD反向延长线上取点A′,B′,C′,D′,
使得 ;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,所得四边形A′B′C′D′
就是所要求作的图形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
作法3:
(1)在四边形ABCD内任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′,B′,C′,D′,
使得 ;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,所得四边形A′B′C′D′
就是所要求作的图形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:作位似图形的基本步骤:
(1)确定位似中心;
(2)连接图形各顶点与位似中心;
(3)在连接图形各顶点与位似中心的直线上按相似比进行取点;
(4)顺次连接各点,所得图形就是所求的图形;
(5)有时符合条件的位似图形不止一个,有时需要根据题意进行取舍.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.在下列图形中,不是位似图形的是( )
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,点F在BD上,BC,AD相交于点E,且AB∥CD∥EF.图中的位似三角形
有 , , .
△DFE与△DBA
△BFE与△BDC
△AEB与△DEC
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.点A,B,C,D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB
成位似图形,则位似中心为( )
A.点E B.点F
C.点H D.点G
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
4.如图,△ABC与△DEF是位似图形,相似比是1∶2,已知DE=4,则AB的长
是( )
A.2 B.4
C.8 D.1
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
5.如图是△ABC位似图形的几种画法,其中正确的个数是( )
A.1 B.2 C.3 D.4
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
6.已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,
且位似比为1:2.
A
B
C
D
E
F
解:画射线OA,OB,OC;
在射线OA,OB,OC上分别取点D,E,F,
使OA = 2OD,OB = 2OE,OC = 2OF;
顺序连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
0
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.位似图形的概念
如果两个图形不仅是相似图形,而且每组对应点的连线相交于一点,
对应边互相平行,那么这样的两个图形叫做位似图形.
2.位似图形的性质
(1)位似图形一定相似,位似比等于相似比;
(2)位似图形对应点和位似中心在同一条直线上;
(3)任意一对对应点到位似中心的距离之比等于位似比或相似比;
(4)对应线段平行或者在一条直线上.
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.位似图形的画法
(1)确定位似中心;
(2)连接图形各顶点与位似中心;
(3)在连接图形各顶点与位似中心的直线上按相似比进行取点;
(4)顺次连接各点,所得图形就是所求的图形.
