2023-2024学年初中数学人教版九年级下册27.3 位似 第2课时 课件(共16张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册27.3 位似 第2课时 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 325.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 08:42:50 | ||
图片预览




文档简介
(共16张PPT)
第2课时 平面直角坐标系中的位似
第二十七章 相似
27.3 位似
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.掌握图形在平面直角坐标系中的相似变换方法与性质; (重点)
2.会在平面直角坐标系中的进行图形的相似变换,掌握在平面直角
坐标系中相似变换的坐标关系.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.回顾:什么是位似图形?
如果两个图形不仅是相似图形,而且每组对应点的连线相交于一点,
对应边互相平行,那么这样的两个图形叫做位似图形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
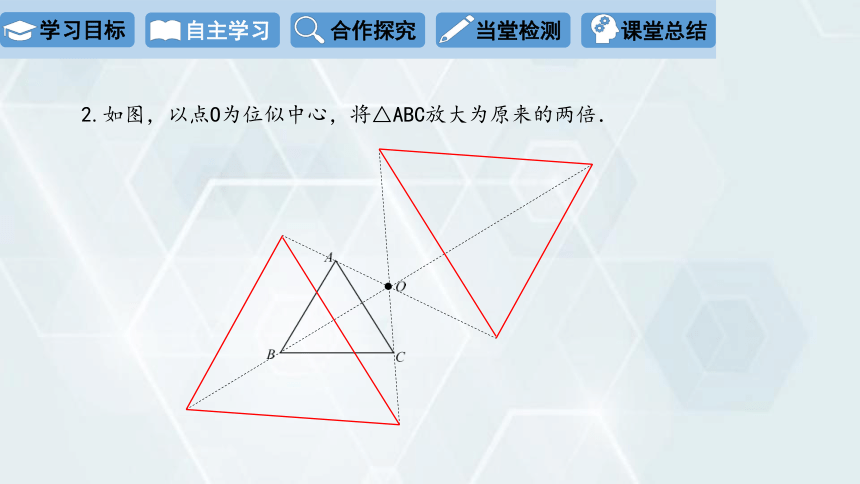
2.如图,以点O为位似中心,将△ABC放大为原来的两倍.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1:探究平面直角坐标系中的位似
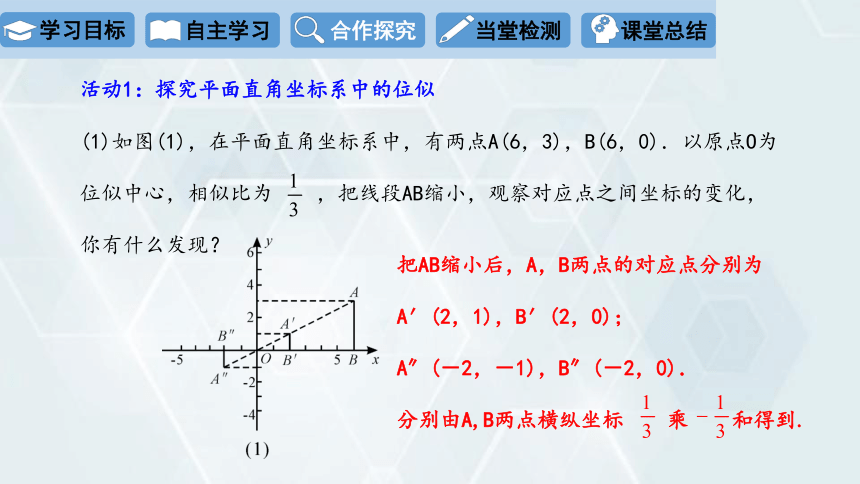
(1)如图(1),在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为
位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,
你有什么发现?
把AB缩小后,A,B两点的对应点分别为
A′(2,1),B′(2,0);
A″(-2,-1),B″(-2,0).
分别由A,B两点横纵坐标 乘 和得到.
合作探究
当堂检测
学习目标
课堂总结
自主学习
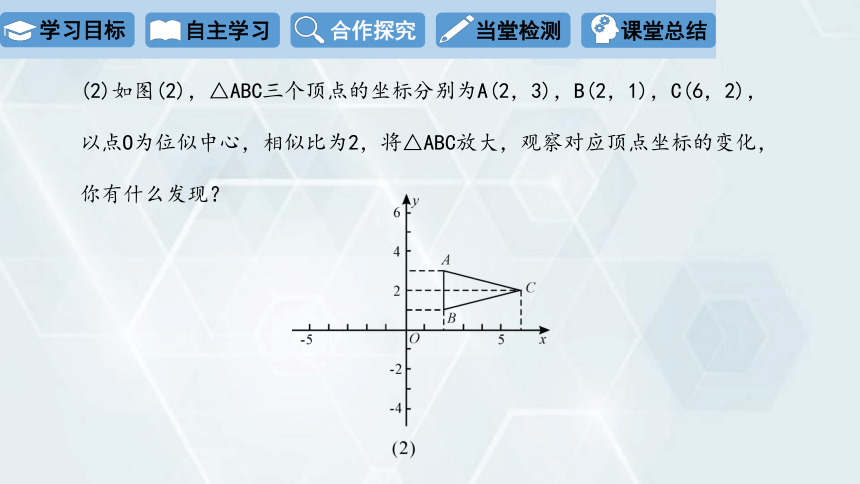
(2)如图(2),△ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),
以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,
你有什么发现?
合作探究
当堂检测
学习目标
课堂总结
自主学习
将△ABC放大后,A,B,C对应的点分别为
A′(4,6),B′(4,2),C′(12,4);
A″(-4,-6),B″(-4,-2),C″(-12,-4).
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:位似变换中对应点的坐标的变化规律:
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,
那么位似图形对应点的坐标的比等于k或-k.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:探究平面直角坐标系中图形的变换
如图,△ABC三个顶点的坐标分别为A(2,3),
B(2,1),C(6,2).
①将△ABC向左平移三个单位得到△A1B1C1,
写出A1,B1,C1三点的坐标;
②写出△ABC关于x轴对称的△A2B2C2的三个
顶点A2,B2,C2的坐标;
③将△ABC绕点O旋转180°得到△A3B3C3,
写出A3,B3,C3三点的坐标.
合作探究
当堂检测
学习目标
课堂总结
自主学习
①将△ABC向左平移三个单位得到△A1B1C1,
则A1(-1,3),B1(-1,1),C1 (3,2);
③将△ABC绕点O旋转180°得到△A3B3C3,
则A3(-2,-3),B3(-2,-1),C3(-6,-2).
②△ABC关于x轴对称的△A2B2C2三个顶点
坐标分别为A2(2,-3),B2(2,-1),C2(6,-2);
1.如图,△ABC的顶点坐标分别为A(-3,2),B(-1,4),C(-2,1),将△ABC以原点O
为位似中心扩大后得到△A'B'C'.若点C'的坐标为(4,-2),则点A'的坐标
为( )
A.(-6,4) B.(6,-6)
C.(3,-2) D.(6,-4)
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
D
2.在平面直角坐标系中,已知点A(6,-3),以原点O为位似中心,相似比为 ,
把线段OA缩小为OA',则点A'的坐标为( )
A.(2,-1)或(-2,-1) B.(-2,1)或(2,1)
C.(2,1)或(-2,-1) D.(2,-1)或(-2,1)
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在平面直角坐标系中,已知点A(4,2),过点A作AB⊥x轴,垂足为B,
将△AOB以坐标原点O为位似中心缩小为原图形的 ,得到△COD,
则OC的长度是 .
4.如图,点E(-6,0),点F(-4,-2),以点O为位似中心,按比例尺
1∶2把△EFO放大,则点F的对应点F'的坐标为 .
(-8,-4)或(8,4)
合作探究
当堂检测
学习目标
课堂总结
自主学习
D
5.如图所示,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点为位似中心,
A'B'与AB的相似比为 ,得到线段A'B',正确的画法是( )
合作探究
当堂检测
学习目标
课堂总结
自主学习
6.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,1),B(1,-2).
以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1,使它与△OAB的
相似比为2∶1,并分别写出点A,B的对应点A1,B1的坐标.
A1
B1
如图,△OA1B1为所作,
点A1,B1的坐标分别为
(4,2),(2,-4)
合作探究
当堂检测
学习目标
课堂总结
自主学习
点的坐标变化的规律
在平面直角坐标系中,作一个图形关于原点O的位似图形,相似比为k(k>0),
可以先找到“关键点”,然后同向直接将坐标乘以相似比k(反向直接将坐标
乘以-k),描出点的位置后连线即可.
第2课时 平面直角坐标系中的位似
第二十七章 相似
27.3 位似
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.掌握图形在平面直角坐标系中的相似变换方法与性质; (重点)
2.会在平面直角坐标系中的进行图形的相似变换,掌握在平面直角
坐标系中相似变换的坐标关系.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.回顾:什么是位似图形?
如果两个图形不仅是相似图形,而且每组对应点的连线相交于一点,
对应边互相平行,那么这样的两个图形叫做位似图形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.如图,以点O为位似中心,将△ABC放大为原来的两倍.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1:探究平面直角坐标系中的位似
(1)如图(1),在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为
位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,
你有什么发现?
把AB缩小后,A,B两点的对应点分别为
A′(2,1),B′(2,0);
A″(-2,-1),B″(-2,0).
分别由A,B两点横纵坐标 乘 和得到.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2)如图(2),△ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),
以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,
你有什么发现?
合作探究
当堂检测
学习目标
课堂总结
自主学习
将△ABC放大后,A,B,C对应的点分别为
A′(4,6),B′(4,2),C′(12,4);
A″(-4,-6),B″(-4,-2),C″(-12,-4).
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:位似变换中对应点的坐标的变化规律:
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,
那么位似图形对应点的坐标的比等于k或-k.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:探究平面直角坐标系中图形的变换
如图,△ABC三个顶点的坐标分别为A(2,3),
B(2,1),C(6,2).
①将△ABC向左平移三个单位得到△A1B1C1,
写出A1,B1,C1三点的坐标;
②写出△ABC关于x轴对称的△A2B2C2的三个
顶点A2,B2,C2的坐标;
③将△ABC绕点O旋转180°得到△A3B3C3,
写出A3,B3,C3三点的坐标.
合作探究
当堂检测
学习目标
课堂总结
自主学习
①将△ABC向左平移三个单位得到△A1B1C1,
则A1(-1,3),B1(-1,1),C1 (3,2);
③将△ABC绕点O旋转180°得到△A3B3C3,
则A3(-2,-3),B3(-2,-1),C3(-6,-2).
②△ABC关于x轴对称的△A2B2C2三个顶点
坐标分别为A2(2,-3),B2(2,-1),C2(6,-2);
1.如图,△ABC的顶点坐标分别为A(-3,2),B(-1,4),C(-2,1),将△ABC以原点O
为位似中心扩大后得到△A'B'C'.若点C'的坐标为(4,-2),则点A'的坐标
为( )
A.(-6,4) B.(6,-6)
C.(3,-2) D.(6,-4)
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
D
2.在平面直角坐标系中,已知点A(6,-3),以原点O为位似中心,相似比为 ,
把线段OA缩小为OA',则点A'的坐标为( )
A.(2,-1)或(-2,-1) B.(-2,1)或(2,1)
C.(2,1)或(-2,-1) D.(2,-1)或(-2,1)
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在平面直角坐标系中,已知点A(4,2),过点A作AB⊥x轴,垂足为B,
将△AOB以坐标原点O为位似中心缩小为原图形的 ,得到△COD,
则OC的长度是 .
4.如图,点E(-6,0),点F(-4,-2),以点O为位似中心,按比例尺
1∶2把△EFO放大,则点F的对应点F'的坐标为 .
(-8,-4)或(8,4)
合作探究
当堂检测
学习目标
课堂总结
自主学习
D
5.如图所示,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点为位似中心,
A'B'与AB的相似比为 ,得到线段A'B',正确的画法是( )
合作探究
当堂检测
学习目标
课堂总结
自主学习
6.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,1),B(1,-2).
以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1,使它与△OAB的
相似比为2∶1,并分别写出点A,B的对应点A1,B1的坐标.
A1
B1
如图,△OA1B1为所作,
点A1,B1的坐标分别为
(4,2),(2,-4)
合作探究
当堂检测
学习目标
课堂总结
自主学习
点的坐标变化的规律
在平面直角坐标系中,作一个图形关于原点O的位似图形,相似比为k(k>0),
可以先找到“关键点”,然后同向直接将坐标乘以相似比k(反向直接将坐标
乘以-k),描出点的位置后连线即可.
