物理人教版(2019)选择性必修第一册4.1光的折射(共26张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册4.1光的折射(共26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 28.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-31 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
4.1光的折射
第四章 光
思考:放入水中的筷子为什么看起来像是被折断了?
筷子“弯折”
思考:水中的射水鱼看到小昆虫在什么位置?是在昆虫的上方还是下方?
射水鱼
一、折射定律
1.1 光的反射、折射现象
光从第 1 种介质射到该介质与第 2 种介质的分界面时,一部分光会返回到第1种介质,这个现象叫作光的反射;另一部分光会进入第2种介质,这个现象叫作光的折射。
一、折射定律
演示实验:
改变入射角,且测出入射角与折射角的大小,找出这些数据间的关系。
空气
玻璃
光由空气射入玻璃中
1.1 光的反射、折射现象
一、折射定律
1.2 光的折射定律
实验数据
入射角θ1 折射角θ2 θ1/θ2 sinθ1/ sinθ2
10° 6.7° 1.50 1.49
20° 13.3° 1.50 1.49
30° 19.6° 1.53 1.49
40° 25.2° 1.59 1.51
50° 30.7° 1.63 1.50
60° 35.1° 1.67 1.51
70° 38.6° 1.81 1.50
80° 40.6° 1.97 1.51
(1)折射光线与入射光线、法线处在同一平面内;
(2)折射光线与入射光线分别位于法线的两侧;
(3)当光从空气斜射入玻璃中时,折射角小于入射角
(4)当光从玻璃斜射入空气中时,折射角大于入射角
(5)入射角的正弦与折射角的正弦成正比。即
一、折射定律
n12是比例常数,与入射角和折射角无关,只与两种介质的性质有关。
定律内容
1.2 光的折射定律
斯涅耳定律
一、折射定律
1.2 光的折射定律
折射光路是可逆的
i
r
空气
水
(1)折射现象中光路是可逆的;
(2)光的传播方向:光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(3)光的传播速度:光从一种介质进入另一种介质时,传播速度一定发生变化,当光垂直界面入射时,光的传播方向虽然不变,但也属于折射,光传播的速度发生变化。
一、折射定律
1.2 光的折射定律
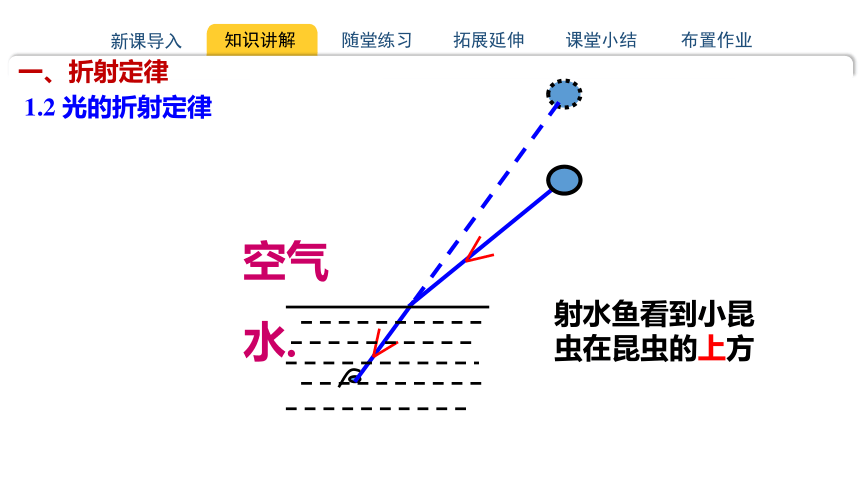
射水鱼看到小昆虫在昆虫的上方
水.
空气
比实际物体位置偏上,看起来比实际深度浅。
想一想:水下的鱼看起来比实际的深度深还是浅?
一、折射定律
1.2 光的折射定律
二、折射率
2.1 折射率
光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做介质的绝对折射率,简称折射率。
研究表明,某种介质的折射率,等于光在真空中的传播速度c跟光在这种介质中的传播速度v之比。即:
n
c
v
=
说明:(1)n的大小与θ1和θ2无关,与介质和入射光的频率有关,对于确定的介质,n是定值,不能说n∝sinθ1或n∝1/sinθ2,
(2)折射率无单位,任何介质的折射率皆大于1。
(3)折射率反映介质对光的偏折作用,n越大光线偏折越厉害。
二、折射率
2.1 折射率
思考:(1)为什么任何介质的折射率都大于1?
(2)光在同一均匀介质中传播时,介质对光所呈现出来的折射率n是多少
(3)光由其他介质射入空气时, 是否还适用,如果适用θ1、θ2 分别应是什么角?
答案:(1)光在真空中的传播速度为c ,而在其它介质中,光的传播速度v(2)同一均匀介质中光速相同,n=1。
(3)适用,θ1应为折射角,θ2应为入射角。
二、折射率
2.2常见介质的折射率
真空的折射率为 1,空气的折射率近似为 1
三、测量玻璃的折射率
2.实验器材
玻璃砖、白 纸、大头针若干、铅笔、直尺、量角器。
3.实验原理
1.实验目的 测定玻璃的折射率。
用插针法确定光路,找出跟入射光线相对应的出射光线,用量角器测入射角θ1和折射角θ2,根据折射定律计算出玻璃的折射率
三、测量玻璃的折射率
4.实验步骤
(1)铺纸(将白纸用图钉固定在木板上);
(2)在白纸上画一条线a作为界面,过a上的一点O(作为入射点)画法线NN′,并画AO作为入射光线;
(3)把玻璃砖放在白纸上,使它的一边与a对齐(确保O为实际入射点) ,确定玻璃砖的另一界面a′(确保出射点准确) ;
(4)在直线AO上竖直插大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线让P2挡住P1的像。再在另一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3、P2、P1的像,记下P3、P4位置;
三、测量玻璃的折射率
4.实验步骤
(5)移去大头针和玻璃砖,过P3、P4所在处作直线DC与a′交于O′(作为实际出射点),直线O′D代表沿AO方向的入射光通过玻璃砖后的传播方向;
(6)连接OO′,入射角 1=∠AON ,折射角 2= ∠N′OO′,用量角器量出入射角和折射角,求出对应的正弦值,记录在表格中;
(7)用上述方法求出入射角分别为300、450、600时的折射角,查出它们的正弦值,填入表格中;
(8)算出不同入射角时的入射角与折射角的正弦比值,最后求出几次实验的平均值为折射率.
1.平均值法
算出不同入射角时的比值 ,最后求出在几次实验中所测的 平均值,即为玻璃砖的折射率。
三、测量玻璃的折射率
5.数据处理
2.图象法
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜率k,则 ,故玻璃砖折射率 。
三、测量玻璃的折射率
5.数据处理
3.作图法
在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点、OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图 所示。由于 ,且CO=DO,所以折射率 。
三、测量玻璃的折射率
6.注意事项
(1)实验时,尽可能将大头针竖直插在纸上,且P1和P2之间,P2与O点之间,P3与P4之间,P3与O′点之间距离要稍大一些。
(2)入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大,也不宜太小。
(3)在操作时,手不能触摸玻璃砖的光洁面。更不能把玻璃砖界面当尺子画界线。
(4)在实验过程中,玻璃砖与白纸的相对位置不能改变。
(5)玻璃砖应选用宽度较大的,宜在5 cm以上。若宽度太小,则测量误差较大。
三、测量玻璃的折射率
7.误差分析
(1)入射光线和出射光线确定得不够精确,因此要求插大头针时,两大头针间距应适当大一些。
(2)入射角和折射角的测量造成误差,故入射角应适当大些,以减小测量的相对误差。
【典例1】 如图所示 ,一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB 方向看去,恰好看到桶底上的点C,C、B两点相距 。求油的折射率和光在油中传播的速度。
解:因为底面直径与桶高相等,所以∠AON =∠BON′= 45
由ON′= 2CN′可知
因此,油的折射率
所以光在油中的传播速度
【典例2】某同学用插针法测定一半圆形玻璃砖的折射率,实验后留下的痕迹如图所示,设AB的长度为l1,AO的长度为l2,CD的长度为l3,DO的长度为l4,为较方便地表示出玻璃砖的折射率,只需用刻度尺测量____和____(均选填“l1”“l2” “l3”或“l4”),则玻璃砖的折射率可表示为________。
答案:
【典例3】学校开展研究性学习,某研究小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示。在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2,并保持P1、P2位置不变,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2的像,同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可以直接读出液体折射率的值,则:
(1)若∠AOF=30°,OP3与OC的夹角为30°,则P3处所对应的折射率的值为________。
(2)图中P3、P4两位置________处所对应的折射率大。
(3)作AO的延长线交圆周于点K,点K处所对应的折射率的值应为________。
答案:(1) (2)P4 (3)1
光的折射
折射定律
测量玻璃的折射率
折射率
【练习1】某同学做测定玻璃折射率实验时,用他测得的多组入射角θ1与折射角θ2作出sinθ1-sinθ2图像,如图所示,则下列判断正确的是( )
A.他做实验时,研究的是光从空气射入玻璃的折射现象
B.玻璃的折射率为0.67
C.玻璃的折射率为1.5
D.他做实验时,研究的是光从玻璃射入空气的折射现象
AC
【练习2】如图所示,单色光沿AO从空气射入水中,以O点为圆心,作两半径分别为R和r(R>r)的同心圆,大圆与入射光线相交于A,与折射光线相交于B,小圆与AO延长线相交于M,BM连线恰好和水平界面垂直,垂足为N,则下列说法正确的是( )
A.水的折射率
B.光线从空气中进入水中,频率变大了
C.光线在AO段的传播时间tAO的大于在OB段的传播时间tOB
D.由于数据不足,无法确定入射角和折射角的大小,故无法计算折射率
A
4.1光的折射
第四章 光
思考:放入水中的筷子为什么看起来像是被折断了?
筷子“弯折”
思考:水中的射水鱼看到小昆虫在什么位置?是在昆虫的上方还是下方?
射水鱼
一、折射定律
1.1 光的反射、折射现象
光从第 1 种介质射到该介质与第 2 种介质的分界面时,一部分光会返回到第1种介质,这个现象叫作光的反射;另一部分光会进入第2种介质,这个现象叫作光的折射。
一、折射定律
演示实验:
改变入射角,且测出入射角与折射角的大小,找出这些数据间的关系。
空气
玻璃
光由空气射入玻璃中
1.1 光的反射、折射现象
一、折射定律
1.2 光的折射定律
实验数据
入射角θ1 折射角θ2 θ1/θ2 sinθ1/ sinθ2
10° 6.7° 1.50 1.49
20° 13.3° 1.50 1.49
30° 19.6° 1.53 1.49
40° 25.2° 1.59 1.51
50° 30.7° 1.63 1.50
60° 35.1° 1.67 1.51
70° 38.6° 1.81 1.50
80° 40.6° 1.97 1.51
(1)折射光线与入射光线、法线处在同一平面内;
(2)折射光线与入射光线分别位于法线的两侧;
(3)当光从空气斜射入玻璃中时,折射角小于入射角
(4)当光从玻璃斜射入空气中时,折射角大于入射角
(5)入射角的正弦与折射角的正弦成正比。即
一、折射定律
n12是比例常数,与入射角和折射角无关,只与两种介质的性质有关。
定律内容
1.2 光的折射定律
斯涅耳定律
一、折射定律
1.2 光的折射定律
折射光路是可逆的
i
r
空气
水
(1)折射现象中光路是可逆的;
(2)光的传播方向:光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(3)光的传播速度:光从一种介质进入另一种介质时,传播速度一定发生变化,当光垂直界面入射时,光的传播方向虽然不变,但也属于折射,光传播的速度发生变化。
一、折射定律
1.2 光的折射定律
射水鱼看到小昆虫在昆虫的上方
水.
空气
比实际物体位置偏上,看起来比实际深度浅。
想一想:水下的鱼看起来比实际的深度深还是浅?
一、折射定律
1.2 光的折射定律
二、折射率
2.1 折射率
光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做介质的绝对折射率,简称折射率。
研究表明,某种介质的折射率,等于光在真空中的传播速度c跟光在这种介质中的传播速度v之比。即:
n
c
v
=
说明:(1)n的大小与θ1和θ2无关,与介质和入射光的频率有关,对于确定的介质,n是定值,不能说n∝sinθ1或n∝1/sinθ2,
(2)折射率无单位,任何介质的折射率皆大于1。
(3)折射率反映介质对光的偏折作用,n越大光线偏折越厉害。
二、折射率
2.1 折射率
思考:(1)为什么任何介质的折射率都大于1?
(2)光在同一均匀介质中传播时,介质对光所呈现出来的折射率n是多少
(3)光由其他介质射入空气时, 是否还适用,如果适用θ1、θ2 分别应是什么角?
答案:(1)光在真空中的传播速度为c ,而在其它介质中,光的传播速度v
(3)适用,θ1应为折射角,θ2应为入射角。
二、折射率
2.2常见介质的折射率
真空的折射率为 1,空气的折射率近似为 1
三、测量玻璃的折射率
2.实验器材
玻璃砖、白 纸、大头针若干、铅笔、直尺、量角器。
3.实验原理
1.实验目的 测定玻璃的折射率。
用插针法确定光路,找出跟入射光线相对应的出射光线,用量角器测入射角θ1和折射角θ2,根据折射定律计算出玻璃的折射率
三、测量玻璃的折射率
4.实验步骤
(1)铺纸(将白纸用图钉固定在木板上);
(2)在白纸上画一条线a作为界面,过a上的一点O(作为入射点)画法线NN′,并画AO作为入射光线;
(3)把玻璃砖放在白纸上,使它的一边与a对齐(确保O为实际入射点) ,确定玻璃砖的另一界面a′(确保出射点准确) ;
(4)在直线AO上竖直插大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线让P2挡住P1的像。再在另一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3、P2、P1的像,记下P3、P4位置;
三、测量玻璃的折射率
4.实验步骤
(5)移去大头针和玻璃砖,过P3、P4所在处作直线DC与a′交于O′(作为实际出射点),直线O′D代表沿AO方向的入射光通过玻璃砖后的传播方向;
(6)连接OO′,入射角 1=∠AON ,折射角 2= ∠N′OO′,用量角器量出入射角和折射角,求出对应的正弦值,记录在表格中;
(7)用上述方法求出入射角分别为300、450、600时的折射角,查出它们的正弦值,填入表格中;
(8)算出不同入射角时的入射角与折射角的正弦比值,最后求出几次实验的平均值为折射率.
1.平均值法
算出不同入射角时的比值 ,最后求出在几次实验中所测的 平均值,即为玻璃砖的折射率。
三、测量玻璃的折射率
5.数据处理
2.图象法
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜率k,则 ,故玻璃砖折射率 。
三、测量玻璃的折射率
5.数据处理
3.作图法
在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点、OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图 所示。由于 ,且CO=DO,所以折射率 。
三、测量玻璃的折射率
6.注意事项
(1)实验时,尽可能将大头针竖直插在纸上,且P1和P2之间,P2与O点之间,P3与P4之间,P3与O′点之间距离要稍大一些。
(2)入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大,也不宜太小。
(3)在操作时,手不能触摸玻璃砖的光洁面。更不能把玻璃砖界面当尺子画界线。
(4)在实验过程中,玻璃砖与白纸的相对位置不能改变。
(5)玻璃砖应选用宽度较大的,宜在5 cm以上。若宽度太小,则测量误差较大。
三、测量玻璃的折射率
7.误差分析
(1)入射光线和出射光线确定得不够精确,因此要求插大头针时,两大头针间距应适当大一些。
(2)入射角和折射角的测量造成误差,故入射角应适当大些,以减小测量的相对误差。
【典例1】 如图所示 ,一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB 方向看去,恰好看到桶底上的点C,C、B两点相距 。求油的折射率和光在油中传播的速度。
解:因为底面直径与桶高相等,所以∠AON =∠BON′= 45
由ON′= 2CN′可知
因此,油的折射率
所以光在油中的传播速度
【典例2】某同学用插针法测定一半圆形玻璃砖的折射率,实验后留下的痕迹如图所示,设AB的长度为l1,AO的长度为l2,CD的长度为l3,DO的长度为l4,为较方便地表示出玻璃砖的折射率,只需用刻度尺测量____和____(均选填“l1”“l2” “l3”或“l4”),则玻璃砖的折射率可表示为________。
答案:
【典例3】学校开展研究性学习,某研究小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示。在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2,并保持P1、P2位置不变,每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2的像,同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可以直接读出液体折射率的值,则:
(1)若∠AOF=30°,OP3与OC的夹角为30°,则P3处所对应的折射率的值为________。
(2)图中P3、P4两位置________处所对应的折射率大。
(3)作AO的延长线交圆周于点K,点K处所对应的折射率的值应为________。
答案:(1) (2)P4 (3)1
光的折射
折射定律
测量玻璃的折射率
折射率
【练习1】某同学做测定玻璃折射率实验时,用他测得的多组入射角θ1与折射角θ2作出sinθ1-sinθ2图像,如图所示,则下列判断正确的是( )
A.他做实验时,研究的是光从空气射入玻璃的折射现象
B.玻璃的折射率为0.67
C.玻璃的折射率为1.5
D.他做实验时,研究的是光从玻璃射入空气的折射现象
AC
【练习2】如图所示,单色光沿AO从空气射入水中,以O点为圆心,作两半径分别为R和r(R>r)的同心圆,大圆与入射光线相交于A,与折射光线相交于B,小圆与AO延长线相交于M,BM连线恰好和水平界面垂直,垂足为N,则下列说法正确的是( )
A.水的折射率
B.光线从空气中进入水中,频率变大了
C.光线在AO段的传播时间tAO的大于在OB段的传播时间tOB
D.由于数据不足,无法确定入射角和折射角的大小,故无法计算折射率
A
