物理人教版(2019)必修第一册4.5牛顿运动定律的应用六大专题(共57张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第一册4.5牛顿运动定律的应用六大专题(共57张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-31 00:00:00 | ||
图片预览







文档简介
(共57张PPT)
牛顿运动定律六大专题
专题一、动力学图像专题
1、常见的图像形式
在动力学与运动学问题中,常见、常用的图像是位移图像(x-t图像)、速度图像(v-t图像)和力的图像(F-t图像)等,这些图像反映的是物体的运动规律、受力规律,而绝非代表物体的运动轨迹.
2、解决图像综合问题的关键
(1)把图像与具体的题意、情境结合起来,明确图像的物理意义,明确图像所反映的物理过程.
(2)特别注意图像中的点、线段、斜率、截距、交点、拐点、面积等方面了解图像给出的信息,再利用共点力平衡、牛顿运动定律及运动学公式解题.
【例题】一质量为m=1 kg的物体在水平恒力F作用下沿直线水平运动,1 s末撤去恒力F,其v-t图像如图所示,则恒力F和物体所受阻力Ff的大小是( )
A.F=9 N,Ff=2 N B.F=8 N,Ff=3 N
C.F=8 N,Ff=2 N D.F=9 N,Ff=3 N
解析:由v-t图像可知,0~1 s内,物体做匀加速直线运动,共加速度大小为a1= = m/s2=6 m/s2;1~3 s内,物体做匀减速直线运动,其加速度的大小为a2= m/s2=3 m/s2.根据牛顿第二定律,0~1 s有F-Ff=ma1,1~3 s有Ff=ma2,解得F=9 N,Ff=3 N.故D正确,A、B、C错误.
D
解析:
【例题】粗糙的水平地面上一物体在水平拉力作用下做直线运动,水平拉力F及运动速度v随时间变化的图像如图甲、乙所示.取重力加速度g=10 m/s2,求:
(1)前2 s内物体运动的加速度和位移大小;
(2)物体的质量m和物体与地面间的动摩擦因数μ.
(1)由v-t图像可知,前2 s内物体运动的加速度为
a== m/s2=2 m/s2
前2 s内物体运动的位移为x= at2= ×2×22 m=4 m.
(2)物体受力如图所示.对于前2 s,由牛顿第二定律得F1-Ff=ma,其中Ff=μmg
2 s后物体做匀速直线运动,由二力平衡条件得F2=Ff
由F - t图像知F1=15 N,F2=5 N
代入数据解得m=5 kg,μ=0.1.
专题二、等高斜面及等底斜面专题
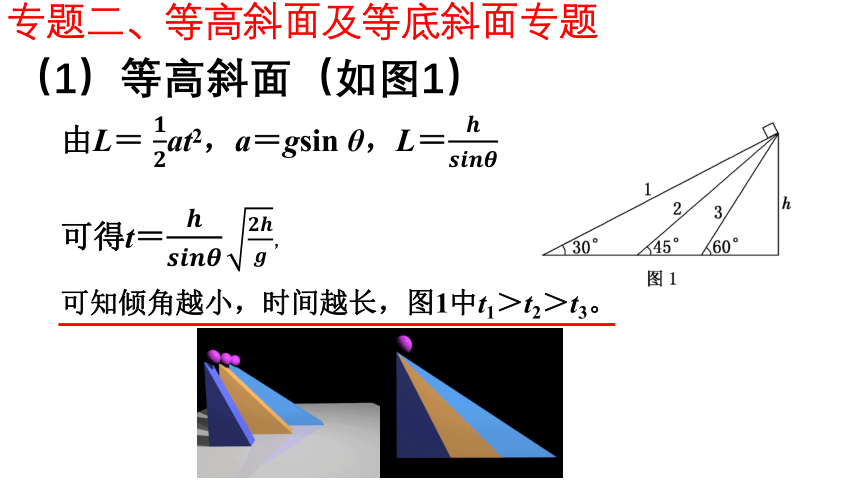
(1)等高斜面(如图1)
由L= at2,a=gsin θ,L=
可得t= ,
可知倾角越小,时间越长,图1中t1>t2>t3。
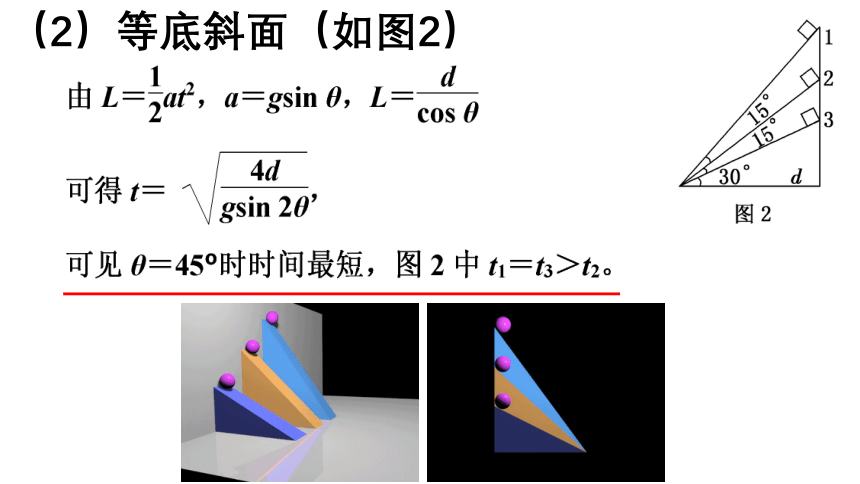
(2)等底斜面(如图2)
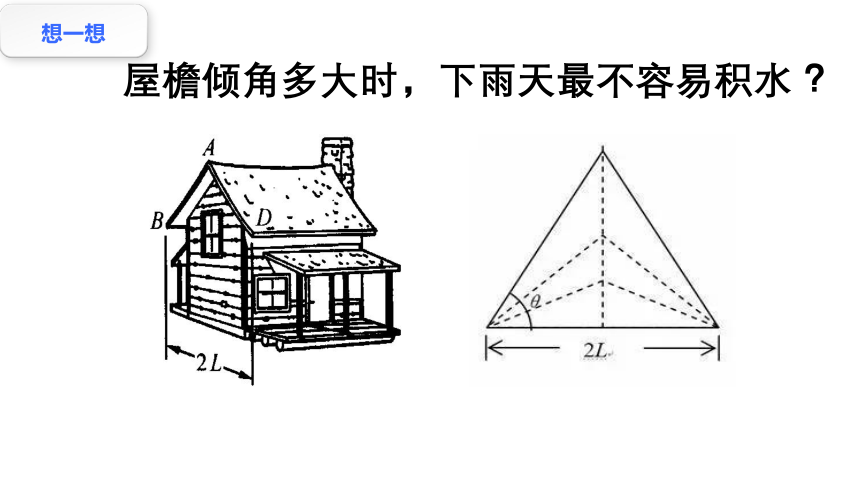
屋檐倾角多大时,下雨天最不容易积水 ?
想一想
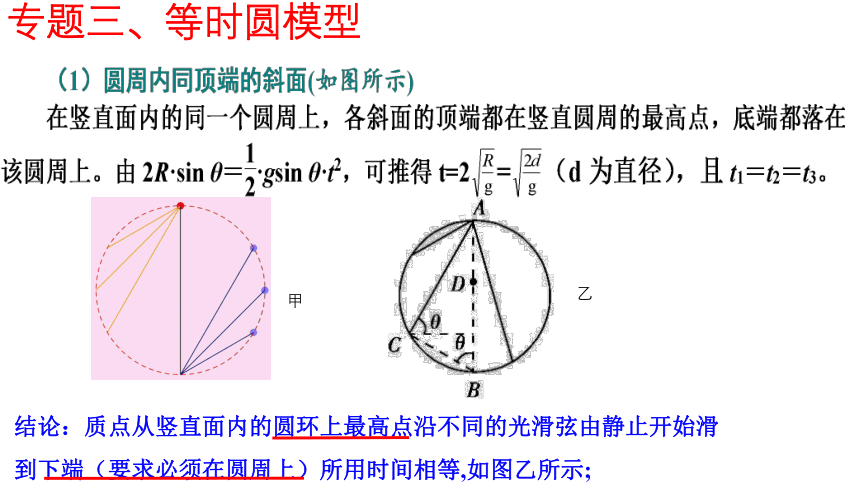
专题三、等时圆模型
甲
乙
结论:质点从竖直面内的圆环上最高点沿不同的光滑弦由静止开始滑
到下端(要求必须在圆周上)所用时间相等,如图乙所示;
(2)圆周内同最底端的斜面(如图所示)
在竖直面内的同一个圆周上,各斜面的底端都在竖直圆周的最低点,顶端都源自该圆周上的不同点。同理可推得
t1=t2=t3。
质点从竖直面内的圆环上沿不同的光滑弦上端(要求必须在圆周上)由静止开始滑到环的最低点所用时间相等,如图甲所示;
实验中摩擦等因素会对运动时间产生影响
(3)双圆周内斜面(如图所示)
在竖直面内两个圆,两圆心在同一竖直线上且两圆相切。各斜面过两圆的公共切点且顶端源自上方圆周上某点,底端落在下方圆周上的相应位置。可推得t1=t2=t3。
两个竖直面内的圆环相切且两环的竖直直径均过切点,质点沿不同的光滑弦上端(圆周上)由静止开始经切点滑到下端(圆周上)所用时间相等,如图丙所示。
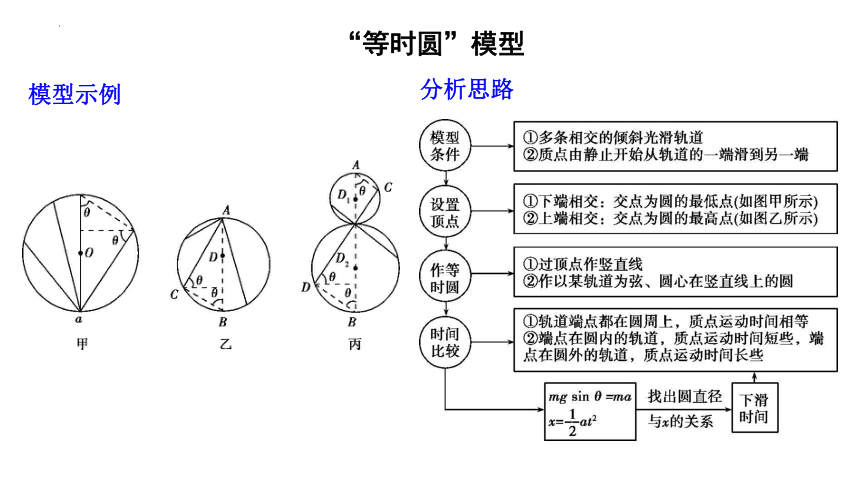
“等时圆”模型
模型示例
分析思路
O
A
O
O
B
外长
内短
等时
等时
等时
等时圆的构建和内外点的时间比较
等时轨道的构建和时间的定性判断
设置顶点1,过顶点1作竖直线
设置顶点2,过顶点2作轨道垂线
找圆心,作等时圆
找等时点和确定非等时点,在圆上等时;圆内时短;圆外时长
【例题】如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点。竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心。已知在同一时刻a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点;c球由C点自由下落到M点。则 ( )
A.a球最先到达M点
B.b球最先到达M点
C.c球最先到达M点
D.b球和c球都可能最先到达M点
C
【例题】[构造等时圆]如图所示,固定支架ACB中,AC竖直,AB为光滑钢丝,AC=BC=l,一穿在钢丝中的小球从A点静止出发,则它滑到B点的时间t为 ( )
A. B. C.2 D.
C
解析 AC=BC=l,以C点为圆心、长度l为半径画圆,则A、B两点均在圆周
上,所以t= =2 ,C正确。
【例题】如图,在斜坡上有一根旗杆长为L,现有一个小环从旗杆顶部沿一根光滑钢丝AB滑至斜坡底部,又知OB=L。求小环从A滑到B的时间。
(1)连接体模型:两个或两个以上相互作用的物体组成的整体叫连接体。常见模型如图所示。
专题四、连接体模型
1.光滑平面内上的绳连接体:
B
A
F
整体法:F=(mA+mB)a
隔离B:TAB=mBa
得:TAB=mB
TAB=
条件:μ=0
问题:求AB间绳的拉力TAB
若μ≠0,TAB表达式是?
模型一:弹力连接体(加速度相同)
2.粗糙平面内上的绳连接体:
B
A
F
得:TAB=mB
TAB=
条件:μ≠0(且A、B与地面的摩擦因数相同)
问题:求AB间绳的拉力TAB
整体法:F-μ(mA+mB)g=(mA+mB)a
隔离B:TAB-μmBg=mBa
3.拓展
(2)平面上的轻杆连接体
B
A
F
TAB=
(不受摩擦影响即μ 相同)
TAB=
(不受摩擦影响即μ 相同)
(1)平面上的弹簧连接体
TAB=
(不受摩擦影响即μ 相同)
(3)平面上的推压连接体
TAB=
(不受摩擦影响即μ 相同)
TAB=
(不受摩擦影响即μ 相同)
(5)竖直面上的连接体
(4)斜面上的连接体
A
B
1.只研究F1的作用,M、m间的作用力:T1=
2.只研究F2的作用,M、m间的作用力:T2=
3.F1,F2的共同作用是增加1、2间的作用力,T=T1+T2=
(6)若μ=0且F1 > F2
反向相加同向相减
拓展:若有摩擦力且μ不相同
4.结论:
由外力F驱动的弹力连接体模型中,物体之间的内力按质量分配,离外力越远(质量越小)越小
① 一分为二定远近;反向相加同向相减
②
T内=F
m远
m总
5.做题步骤:
1 如图,两物块P、Q置于水平地面上,其质量分别为m、2m,两者之间用水平轻绳连接。两物块与地面之间的动摩擦因数均为μ,重力加速度大小为g,现对Q施加一水平向右的拉力F,使两物块做匀加速直线运动,轻绳的张力大小为( )
典例
D
②
T内= F
m远
m总
① 一分为二定远近:p为离F远的物体
T内= F
m
3m
T内= F
1
3
2.水平拉力F拉着A、B、C三个物体在粗糙地面向右做匀加速直线运动,物体与接触面动摩擦因数为μ,则:
T2=
T1=
F
mB+mc
mA+mB+mc
F
T1
T2
A
B
C
拓展
研究T1,将B、C看成整体,该整体为远离F的物体
2.水平拉力F拉着A、B、C三个物体在粗糙地面向右做匀加速直线运动,物体与接触面动摩擦因数为μ,则:
T2=
F
T1
T2
A
B
C
F
mc
mA+mB+mc
研究T2,将A、B看成整体,物体C为远离F的物体
T1=
F
mB+mc
mA+mB+mc
3.如图所示,n个质量均为m的相同木块并排放在水平地面上,当木块1受到水平恒力F而向右加速运动时,木块3对木块4的作用力F'为( )
A.不论是否光滑,均为F
B.若光滑,为F;若不光滑,小于F
C.不论是否光滑,均为
D.不论是否光滑,均为(1- )F
3F
n
3
n
1
2
3
4
n
F
3.如图所示,n个质量均为m的相同木块并排放在水平地面上,当木块1受到水平恒力F而向右加速运动时,木块3对木块4的作用力F'为( )
D
1
2
3
4
n
F
A.不论是否光滑,均为F
B.若光滑,为F;若不光滑,小于F
C.不论是否光滑,均为
D.不论是否光滑,均为(1- )F
3F
n
3
n
研究3、4间的作用力,将1~3和4~n看成两个整体,4~n整体为远离F的物体
F'= F
(n-3)m
nm
3
=(1- )F
n
4.如图所示,两个质量相同的物体1和2紧靠在一起,放在光滑水平桌面上,如果它们分别受到水平推力F1和F2作用,而且F1>F2,则1施于2的作用力大小为( )
1.只研究F1的作用,1、2间的作用力:T1=
2.只研究F2的作用,1、2间的作用力:T2=
3.F1,F2的共同作用是增加1、2间的作用力,T=T1+T2=
)
C
典例
5.质量分别为m和M的物块A、B用轻弹簧相连,它们的质量之比m∶M=1∶2。如图甲所示,两物块与水平面间的动摩擦因数相同,当用水平力F作用于B上且两物块以相同的加速度向右加速运动时,弹簧的伸长量为x1;如图乙所示,当用同样大小的力F竖直向上拉B且两物块以相同的加速度竖直向上运动时,弹簧的伸长量为x2,则x1∶x2等于( )
A.1∶1 B.1∶2
C.2∶1 D.2∶3
F=k·x1
F=k·x2
A
典例
6.(多选)如图所示,两个质量分别为m1=1 kg、m2=4 kg的物体置于光滑的水平面上,中间用轻弹簧测力计连接。两个大小分别为F1=30 N、F2=20 N的水平拉力分别作用在m1、m2上,则达到稳定状态后,说法正确的是( )
A.弹簧测力计的示数是28 N
B.弹簧测力计的示数是30 N
C.在突然撤去F2的瞬间,m2的加速度大小为5 m/s2
D.在突然撤去F1的瞬间,m1的加速度大小为28 m/s2
1.只研究F1的作用,1、2间的作用力:T1=
2.只研究F2的作用,1、2间的作用力:T2=
3.F1,F2的共同作用是增加1、2间的作用力,T=T1+T2=28N
AD
典例
条件:μ=0
问题:求AB间绳的拉力FAB
隔离A:TAB=mAa
隔离B:mBg-TAB=mBa
TAB= mBg
a
a
若μ≠0,FAB表达式是?
1.光滑接触面上的绳连接体:(加速度大小相同,方向不同)
将mBg当作外力F,结果满足模型一的结论:
TAB=
模型二:弹力连接体(加速度不同)
条件:μ≠0
问题:求AB间绳的拉力FAB
隔离A:TAB-μmAg=mAa
隔离B:mBg-TAB=mBa
a
a
TAB= mBg+ μmAg
2.粗糙接触面上的绳连接体:(加速度大小相同,方向不同)
将mBg当作外力F1,只考虑F1,T1=
将μmAg当作外力F2,只考虑F2,T2=
满足模型一的结论:
TAB=T1+T2
3.斜面上的连接体:(加速度大小相同,方向不同)
条件:μ=0
a
a
θ
条件:μ≠0
a
a
θ
将mBg当作外力F1,只考虑F1,T1=
将mAgsin 当作外力F2,只考虑F2,T2=
满足模型一的结论:TAB=T1+T2
TAB=T1+T2
θ
将mBg当作外力F1,只考虑F1,T1=
将μmAgcos +mAgsin 当作外力F2,只考虑F2,T2=
满足模型一的结论:TAB=T1+T2
θ
θ
4.竖直面上的连接体:(加速度大小相同,方向不同)
a
a
将mBg当作外力F1,只考虑F1,T1=
将mAg当作外力F2,只考虑F2,T2=
满足模型一的结论:TAB=T1+T2
a
a
将mBg当作外力F1,只考虑F1,T1=
将mAg当作外力F2,只考虑F2,T2=
将F当作外力F3,只考虑F3,T3=
满足模型一的结论:TAB=T1+T2-T3
F
典例
A
7.如图所示,物体A重20 N,物体B重5 N,不计一切摩擦和绳的重力,当两物体由静止释放后,物体A的加速度与绳子上的张力分别为(g取10 m/s2)( )
A.6 m/s2,8 N B.10 m/s2,8 N
C.8 m/s2,6 N D.6 m/s2,9 N
将mBg当作外力F1,只考虑F1,T1=
将mAg当作外力F2,只考虑F2,T2=
TAB=T1+T2=8N,aA=6m/s2
模型1 滑块在水平传送带上的运动
1
情景一:无初速的滑块在水平传送带上的运动分析
情景二:与传送带具有同向速度的滑块在水平传送带上的运动分析
情景三:与传送带具有反向速度的滑块在水平传送带上的运动分析
模型2 无初速的滑块在倾斜传送带上的运动
2
情景一:无初速度的滑块在倾斜传送带上由底端向顶端运动的情况分析
情景二:无初速度的滑块在倾斜传送带上由顶端向底端运动的情况分析
情景三:与传送带具有同向速度的滑块在倾斜传送带上的运动情况分析
情景四:与传送带具有反向速度的滑块在倾斜传送带上的运动情况分析
分类——传送带模型
专题五、传送带模型
【情景一】
【模型1】如图所示,传送带从A到B长度为L,传送带以v0的速率顺时针转动.在传送带上端A无初速地放一个质量为m的物体,它与传送带间的动摩擦因数为μ,试分析滑块在传送带上的运动情况.
无初速度的滑块在水平传送带上的运动情况分析
v0
A
B
模型一 水平传送带
无初速度的滑块在水平传送带上的运动情况分析
传送带刚够长
v0
v0
v
t
v0
滑块一直做匀加速
传送带 长度
滑块在传送带上的运动情景
滑块运动情况
滑块运动的v-t图像
注意:滑块在传送带上加速获得的最大速度不大于传送带的速度。
传送带不够长
滑块一直做匀加速
v0
v
t
v
v0
v
传送带足够长
v0
v0
滑块先做匀加速后匀速
v
t
v0
t1
【情景一】
传送带足够长
v0
v0
传送带刚够长
v0
v0
滑块先做匀加速后匀速
滑块一直做匀加速
传送带不够长
滑块一直做匀加速
v0
v
传送带 长度
滑块在传送带上的运动情景
滑块运动情况
滑块运动的v-t图像
与传送带具有同向速度的滑块在水平传送带上的运动分析(v1v0
v
t
v1
t
v
t
v0
t
v1
v
t
v0
t1
t
v1
注意:滑块在传送带上加速时,获得的最大速度不大于传送带的速度。
【情景二】
传送带足够长
v0
v0
传送带刚够长
v0
v0
滑块先做匀减速后匀速
滑块一直做匀减速
传送带不够长
滑块一直做匀减速
v0
v
传送带 长度
滑块在传送带上的运动情景
滑块运动情况
滑块运动的v-t图像
v
t
v0
t1
v1
t
v
t
v0
v1
t
v0
v
t
v1
t
与传送带具有同向速度的滑块在水平传送带上的运动分析(v1>v0)
注意:滑块在传送带上减速时,减速后的最后速度不小于传送带的速度。
【情景二】
【情景三】
与传送带具有反向速度的滑块在水平传送带上的运动分析
【模型1】如图所示,传送带从A到B长度为L,传送带以v0的速率顺(逆)时针转动.一个质量为m的滑块从A端以速度v1滑上传送带,它与传送带间的动摩擦因数为μ,试分析滑块在传送带上的运动情况.
v0
A
B
v1
1
A
B
V=0
v0
V=0
v0
滑块先做匀减速后反向匀加速至v1(v1滑块一直做匀减速
滑块一直做匀减速
v0
v
v
t
-v0
v1
t
v
-v0
t
v1
t
与传送带具有反向速度的滑块在水平传送带上的运动分析
传送带足够长
传送带刚够长
传送带不够长
传送带 长度
滑块在传送带上的运动情景
滑块运动情况
滑块运动的v-t图像
v
t
-v0
t1
v1
t
-v1
滑块先做匀减速后反向匀加速至v0 ,后做匀速(v1>v0)
v
t
-v0
t1
v1
t
【情景三】
【问题一】分析无初速度的滑块在水平传送带上运动的时间.
【模型1】如图所示,传送带从A到B长度为L,传送带以v0的速率顺时针转动.在传送带上端A无初速地放一个质量为m的物体,它与传送带间的动摩擦因数为μ,求物体从A运动到B需要的时间.
A
B
V
【讨论一】传送带“不够长”(物体到达B时,速度仍小于传送带的速度)
G
f
N
物体从A运动到B一直做匀加速,设加速时间为t,则:
得:
【问题一】分析无初速度的滑块在水平传送带上运动的时间.
A
B
V
【讨论二】传送带“刚够长”(物体到B时,速度刚好等于传送带的速度)
G
f
N
物体从A运动到B一直做匀加速,设加速时间为t,则:
得:
得:
【问题一】分析无初速度的滑块在水平传送带上运动的时间.
A
B
V
【讨论三】传送带“足够长”(物体到B前,速度等于传送带的速度,之后由于不再受摩擦力而做匀速运动)
G
f
N
物体做匀加速时间为:
G
N
物体做匀加速位移为:
物体做匀速时间为:
物体从A到B的总时间为:
得:
【结论】无初速度的滑块在水平传送带上的运动的时间
传送带刚够长
v0
v0
传送带 长度
滑块在传送带上的运动情景
滑块运动的时间
传送带不够长
v0
v
传送带足够长
v0
v0
得:
得:
【例1】如图所示,足够长的水平传送带以=2m/s的速度匀速运行。t=0时,在最左端轻放一质量为m的小滑块,t=2s时,传送带突然制动停下。已知滑块与传送带之间的动摩擦因数μ=0.2。下列关于滑块相对地面运动的v-t图像正确的是( )
D
【例2】物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下,则:( )
A. 物块将仍落在Q点
B. 物块将会落在Q点的左边
C. 物块将会落在Q点的右边
D. 物块有可能落不到地面上
P
Q
A
【例3】
B
1.概念:一个物体在另一个物体上发生相对滑动,两者之间有相对运动。问题涉及两个物体、多个过程,两物体的运动时间、速度、位移间有一定的关系。
2.模型的特点:
滑块(视为质点)置于木板上,滑块和木板均相对地面运动,且滑块和木板在摩擦力的相互作用下发生相对滑动。
专题六、板块模型(滑块—木板模型)
x1
模型特点
涉及两个发生相对滑动的物体.
两种位移关系
滑块由滑板的一端运动到另一端的过程中
若滑块和滑板同向运动,位移之差等于板长;
若滑块和滑板相向运动,位移之和等于板长.
设板长为L,滑块位移x1,滑板位移x2
同向运动时:
相向运动时:
x1
x2
L=x1-x2
L=x1+x2
x2
运动演示
易错辨析
同向运动两种类型:
【例1】如图所示,长为L=2m、质量为M=8kg的木板,放在水平地面上,木板向右运动的速度v0=6m/s时,在木板最前端轻放一个大小不计、质量为m=2kg的小物块。木板与地面、物块与木板间的动摩擦因数均为μ=0.2,g=10m/s2。求:
(1)物块的加速度大小a1;
(2)木板的加速度大小a2
(3)物块滑离木板时的时间t。
【例题2】如图所示,物块A、木板B的质量均为m=10kg,不计A的大小,B板长L=3m。开始时A、B均静止。现使A以某一水平初速度从B的最左端开始运动。已知A与B、B与水平面之间的动摩擦因数分别为μ1=0.3和μ2=0.1, g取10 m/s2。
(1)若物块A刚好没有从B上滑下来,则A的初速度多大
(2)若把木板B放在光滑水平面上,让A仍以(1)问中的初速度从B的最左端开始运动,则A能否与B脱离 最终A和B的速度各是多大
牛顿运动定律六大专题
专题一、动力学图像专题
1、常见的图像形式
在动力学与运动学问题中,常见、常用的图像是位移图像(x-t图像)、速度图像(v-t图像)和力的图像(F-t图像)等,这些图像反映的是物体的运动规律、受力规律,而绝非代表物体的运动轨迹.
2、解决图像综合问题的关键
(1)把图像与具体的题意、情境结合起来,明确图像的物理意义,明确图像所反映的物理过程.
(2)特别注意图像中的点、线段、斜率、截距、交点、拐点、面积等方面了解图像给出的信息,再利用共点力平衡、牛顿运动定律及运动学公式解题.
【例题】一质量为m=1 kg的物体在水平恒力F作用下沿直线水平运动,1 s末撤去恒力F,其v-t图像如图所示,则恒力F和物体所受阻力Ff的大小是( )
A.F=9 N,Ff=2 N B.F=8 N,Ff=3 N
C.F=8 N,Ff=2 N D.F=9 N,Ff=3 N
解析:由v-t图像可知,0~1 s内,物体做匀加速直线运动,共加速度大小为a1= = m/s2=6 m/s2;1~3 s内,物体做匀减速直线运动,其加速度的大小为a2= m/s2=3 m/s2.根据牛顿第二定律,0~1 s有F-Ff=ma1,1~3 s有Ff=ma2,解得F=9 N,Ff=3 N.故D正确,A、B、C错误.
D
解析:
【例题】粗糙的水平地面上一物体在水平拉力作用下做直线运动,水平拉力F及运动速度v随时间变化的图像如图甲、乙所示.取重力加速度g=10 m/s2,求:
(1)前2 s内物体运动的加速度和位移大小;
(2)物体的质量m和物体与地面间的动摩擦因数μ.
(1)由v-t图像可知,前2 s内物体运动的加速度为
a== m/s2=2 m/s2
前2 s内物体运动的位移为x= at2= ×2×22 m=4 m.
(2)物体受力如图所示.对于前2 s,由牛顿第二定律得F1-Ff=ma,其中Ff=μmg
2 s后物体做匀速直线运动,由二力平衡条件得F2=Ff
由F - t图像知F1=15 N,F2=5 N
代入数据解得m=5 kg,μ=0.1.
专题二、等高斜面及等底斜面专题
(1)等高斜面(如图1)
由L= at2,a=gsin θ,L=
可得t= ,
可知倾角越小,时间越长,图1中t1>t2>t3。
(2)等底斜面(如图2)
屋檐倾角多大时,下雨天最不容易积水 ?
想一想
专题三、等时圆模型
甲
乙
结论:质点从竖直面内的圆环上最高点沿不同的光滑弦由静止开始滑
到下端(要求必须在圆周上)所用时间相等,如图乙所示;
(2)圆周内同最底端的斜面(如图所示)
在竖直面内的同一个圆周上,各斜面的底端都在竖直圆周的最低点,顶端都源自该圆周上的不同点。同理可推得
t1=t2=t3。
质点从竖直面内的圆环上沿不同的光滑弦上端(要求必须在圆周上)由静止开始滑到环的最低点所用时间相等,如图甲所示;
实验中摩擦等因素会对运动时间产生影响
(3)双圆周内斜面(如图所示)
在竖直面内两个圆,两圆心在同一竖直线上且两圆相切。各斜面过两圆的公共切点且顶端源自上方圆周上某点,底端落在下方圆周上的相应位置。可推得t1=t2=t3。
两个竖直面内的圆环相切且两环的竖直直径均过切点,质点沿不同的光滑弦上端(圆周上)由静止开始经切点滑到下端(圆周上)所用时间相等,如图丙所示。
“等时圆”模型
模型示例
分析思路
O
A
O
O
B
外长
内短
等时
等时
等时
等时圆的构建和内外点的时间比较
等时轨道的构建和时间的定性判断
设置顶点1,过顶点1作竖直线
设置顶点2,过顶点2作轨道垂线
找圆心,作等时圆
找等时点和确定非等时点,在圆上等时;圆内时短;圆外时长
【例题】如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点。竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心。已知在同一时刻a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点;c球由C点自由下落到M点。则 ( )
A.a球最先到达M点
B.b球最先到达M点
C.c球最先到达M点
D.b球和c球都可能最先到达M点
C
【例题】[构造等时圆]如图所示,固定支架ACB中,AC竖直,AB为光滑钢丝,AC=BC=l,一穿在钢丝中的小球从A点静止出发,则它滑到B点的时间t为 ( )
A. B. C.2 D.
C
解析 AC=BC=l,以C点为圆心、长度l为半径画圆,则A、B两点均在圆周
上,所以t= =2 ,C正确。
【例题】如图,在斜坡上有一根旗杆长为L,现有一个小环从旗杆顶部沿一根光滑钢丝AB滑至斜坡底部,又知OB=L。求小环从A滑到B的时间。
(1)连接体模型:两个或两个以上相互作用的物体组成的整体叫连接体。常见模型如图所示。
专题四、连接体模型
1.光滑平面内上的绳连接体:
B
A
F
整体法:F=(mA+mB)a
隔离B:TAB=mBa
得:TAB=mB
TAB=
条件:μ=0
问题:求AB间绳的拉力TAB
若μ≠0,TAB表达式是?
模型一:弹力连接体(加速度相同)
2.粗糙平面内上的绳连接体:
B
A
F
得:TAB=mB
TAB=
条件:μ≠0(且A、B与地面的摩擦因数相同)
问题:求AB间绳的拉力TAB
整体法:F-μ(mA+mB)g=(mA+mB)a
隔离B:TAB-μmBg=mBa
3.拓展
(2)平面上的轻杆连接体
B
A
F
TAB=
(不受摩擦影响即μ 相同)
TAB=
(不受摩擦影响即μ 相同)
(1)平面上的弹簧连接体
TAB=
(不受摩擦影响即μ 相同)
(3)平面上的推压连接体
TAB=
(不受摩擦影响即μ 相同)
TAB=
(不受摩擦影响即μ 相同)
(5)竖直面上的连接体
(4)斜面上的连接体
A
B
1.只研究F1的作用,M、m间的作用力:T1=
2.只研究F2的作用,M、m间的作用力:T2=
3.F1,F2的共同作用是增加1、2间的作用力,T=T1+T2=
(6)若μ=0且F1 > F2
反向相加同向相减
拓展:若有摩擦力且μ不相同
4.结论:
由外力F驱动的弹力连接体模型中,物体之间的内力按质量分配,离外力越远(质量越小)越小
① 一分为二定远近;反向相加同向相减
②
T内=F
m远
m总
5.做题步骤:
1 如图,两物块P、Q置于水平地面上,其质量分别为m、2m,两者之间用水平轻绳连接。两物块与地面之间的动摩擦因数均为μ,重力加速度大小为g,现对Q施加一水平向右的拉力F,使两物块做匀加速直线运动,轻绳的张力大小为( )
典例
D
②
T内= F
m远
m总
① 一分为二定远近:p为离F远的物体
T内= F
m
3m
T内= F
1
3
2.水平拉力F拉着A、B、C三个物体在粗糙地面向右做匀加速直线运动,物体与接触面动摩擦因数为μ,则:
T2=
T1=
F
mB+mc
mA+mB+mc
F
T1
T2
A
B
C
拓展
研究T1,将B、C看成整体,该整体为远离F的物体
2.水平拉力F拉着A、B、C三个物体在粗糙地面向右做匀加速直线运动,物体与接触面动摩擦因数为μ,则:
T2=
F
T1
T2
A
B
C
F
mc
mA+mB+mc
研究T2,将A、B看成整体,物体C为远离F的物体
T1=
F
mB+mc
mA+mB+mc
3.如图所示,n个质量均为m的相同木块并排放在水平地面上,当木块1受到水平恒力F而向右加速运动时,木块3对木块4的作用力F'为( )
A.不论是否光滑,均为F
B.若光滑,为F;若不光滑,小于F
C.不论是否光滑,均为
D.不论是否光滑,均为(1- )F
3F
n
3
n
1
2
3
4
n
F
3.如图所示,n个质量均为m的相同木块并排放在水平地面上,当木块1受到水平恒力F而向右加速运动时,木块3对木块4的作用力F'为( )
D
1
2
3
4
n
F
A.不论是否光滑,均为F
B.若光滑,为F;若不光滑,小于F
C.不论是否光滑,均为
D.不论是否光滑,均为(1- )F
3F
n
3
n
研究3、4间的作用力,将1~3和4~n看成两个整体,4~n整体为远离F的物体
F'= F
(n-3)m
nm
3
=(1- )F
n
4.如图所示,两个质量相同的物体1和2紧靠在一起,放在光滑水平桌面上,如果它们分别受到水平推力F1和F2作用,而且F1>F2,则1施于2的作用力大小为( )
1.只研究F1的作用,1、2间的作用力:T1=
2.只研究F2的作用,1、2间的作用力:T2=
3.F1,F2的共同作用是增加1、2间的作用力,T=T1+T2=
)
C
典例
5.质量分别为m和M的物块A、B用轻弹簧相连,它们的质量之比m∶M=1∶2。如图甲所示,两物块与水平面间的动摩擦因数相同,当用水平力F作用于B上且两物块以相同的加速度向右加速运动时,弹簧的伸长量为x1;如图乙所示,当用同样大小的力F竖直向上拉B且两物块以相同的加速度竖直向上运动时,弹簧的伸长量为x2,则x1∶x2等于( )
A.1∶1 B.1∶2
C.2∶1 D.2∶3
F=k·x1
F=k·x2
A
典例
6.(多选)如图所示,两个质量分别为m1=1 kg、m2=4 kg的物体置于光滑的水平面上,中间用轻弹簧测力计连接。两个大小分别为F1=30 N、F2=20 N的水平拉力分别作用在m1、m2上,则达到稳定状态后,说法正确的是( )
A.弹簧测力计的示数是28 N
B.弹簧测力计的示数是30 N
C.在突然撤去F2的瞬间,m2的加速度大小为5 m/s2
D.在突然撤去F1的瞬间,m1的加速度大小为28 m/s2
1.只研究F1的作用,1、2间的作用力:T1=
2.只研究F2的作用,1、2间的作用力:T2=
3.F1,F2的共同作用是增加1、2间的作用力,T=T1+T2=28N
AD
典例
条件:μ=0
问题:求AB间绳的拉力FAB
隔离A:TAB=mAa
隔离B:mBg-TAB=mBa
TAB= mBg
a
a
若μ≠0,FAB表达式是?
1.光滑接触面上的绳连接体:(加速度大小相同,方向不同)
将mBg当作外力F,结果满足模型一的结论:
TAB=
模型二:弹力连接体(加速度不同)
条件:μ≠0
问题:求AB间绳的拉力FAB
隔离A:TAB-μmAg=mAa
隔离B:mBg-TAB=mBa
a
a
TAB= mBg+ μmAg
2.粗糙接触面上的绳连接体:(加速度大小相同,方向不同)
将mBg当作外力F1,只考虑F1,T1=
将μmAg当作外力F2,只考虑F2,T2=
满足模型一的结论:
TAB=T1+T2
3.斜面上的连接体:(加速度大小相同,方向不同)
条件:μ=0
a
a
θ
条件:μ≠0
a
a
θ
将mBg当作外力F1,只考虑F1,T1=
将mAgsin 当作外力F2,只考虑F2,T2=
满足模型一的结论:TAB=T1+T2
TAB=T1+T2
θ
将mBg当作外力F1,只考虑F1,T1=
将μmAgcos +mAgsin 当作外力F2,只考虑F2,T2=
满足模型一的结论:TAB=T1+T2
θ
θ
4.竖直面上的连接体:(加速度大小相同,方向不同)
a
a
将mBg当作外力F1,只考虑F1,T1=
将mAg当作外力F2,只考虑F2,T2=
满足模型一的结论:TAB=T1+T2
a
a
将mBg当作外力F1,只考虑F1,T1=
将mAg当作外力F2,只考虑F2,T2=
将F当作外力F3,只考虑F3,T3=
满足模型一的结论:TAB=T1+T2-T3
F
典例
A
7.如图所示,物体A重20 N,物体B重5 N,不计一切摩擦和绳的重力,当两物体由静止释放后,物体A的加速度与绳子上的张力分别为(g取10 m/s2)( )
A.6 m/s2,8 N B.10 m/s2,8 N
C.8 m/s2,6 N D.6 m/s2,9 N
将mBg当作外力F1,只考虑F1,T1=
将mAg当作外力F2,只考虑F2,T2=
TAB=T1+T2=8N,aA=6m/s2
模型1 滑块在水平传送带上的运动
1
情景一:无初速的滑块在水平传送带上的运动分析
情景二:与传送带具有同向速度的滑块在水平传送带上的运动分析
情景三:与传送带具有反向速度的滑块在水平传送带上的运动分析
模型2 无初速的滑块在倾斜传送带上的运动
2
情景一:无初速度的滑块在倾斜传送带上由底端向顶端运动的情况分析
情景二:无初速度的滑块在倾斜传送带上由顶端向底端运动的情况分析
情景三:与传送带具有同向速度的滑块在倾斜传送带上的运动情况分析
情景四:与传送带具有反向速度的滑块在倾斜传送带上的运动情况分析
分类——传送带模型
专题五、传送带模型
【情景一】
【模型1】如图所示,传送带从A到B长度为L,传送带以v0的速率顺时针转动.在传送带上端A无初速地放一个质量为m的物体,它与传送带间的动摩擦因数为μ,试分析滑块在传送带上的运动情况.
无初速度的滑块在水平传送带上的运动情况分析
v0
A
B
模型一 水平传送带
无初速度的滑块在水平传送带上的运动情况分析
传送带刚够长
v0
v0
v
t
v0
滑块一直做匀加速
传送带 长度
滑块在传送带上的运动情景
滑块运动情况
滑块运动的v-t图像
注意:滑块在传送带上加速获得的最大速度不大于传送带的速度。
传送带不够长
滑块一直做匀加速
v0
v
t
v
v0
v
传送带足够长
v0
v0
滑块先做匀加速后匀速
v
t
v0
t1
【情景一】
传送带足够长
v0
v0
传送带刚够长
v0
v0
滑块先做匀加速后匀速
滑块一直做匀加速
传送带不够长
滑块一直做匀加速
v0
v
传送带 长度
滑块在传送带上的运动情景
滑块运动情况
滑块运动的v-t图像
与传送带具有同向速度的滑块在水平传送带上的运动分析(v1
v
t
v1
t
v
t
v0
t
v1
v
t
v0
t1
t
v1
注意:滑块在传送带上加速时,获得的最大速度不大于传送带的速度。
【情景二】
传送带足够长
v0
v0
传送带刚够长
v0
v0
滑块先做匀减速后匀速
滑块一直做匀减速
传送带不够长
滑块一直做匀减速
v0
v
传送带 长度
滑块在传送带上的运动情景
滑块运动情况
滑块运动的v-t图像
v
t
v0
t1
v1
t
v
t
v0
v1
t
v0
v
t
v1
t
与传送带具有同向速度的滑块在水平传送带上的运动分析(v1>v0)
注意:滑块在传送带上减速时,减速后的最后速度不小于传送带的速度。
【情景二】
【情景三】
与传送带具有反向速度的滑块在水平传送带上的运动分析
【模型1】如图所示,传送带从A到B长度为L,传送带以v0的速率顺(逆)时针转动.一个质量为m的滑块从A端以速度v1滑上传送带,它与传送带间的动摩擦因数为μ,试分析滑块在传送带上的运动情况.
v0
A
B
v1
1
A
B
V=0
v0
V=0
v0
滑块先做匀减速后反向匀加速至v1(v1
滑块一直做匀减速
v0
v
v
t
-v0
v1
t
v
-v0
t
v1
t
与传送带具有反向速度的滑块在水平传送带上的运动分析
传送带足够长
传送带刚够长
传送带不够长
传送带 长度
滑块在传送带上的运动情景
滑块运动情况
滑块运动的v-t图像
v
t
-v0
t1
v1
t
-v1
滑块先做匀减速后反向匀加速至v0 ,后做匀速(v1>v0)
v
t
-v0
t1
v1
t
【情景三】
【问题一】分析无初速度的滑块在水平传送带上运动的时间.
【模型1】如图所示,传送带从A到B长度为L,传送带以v0的速率顺时针转动.在传送带上端A无初速地放一个质量为m的物体,它与传送带间的动摩擦因数为μ,求物体从A运动到B需要的时间.
A
B
V
【讨论一】传送带“不够长”(物体到达B时,速度仍小于传送带的速度)
G
f
N
物体从A运动到B一直做匀加速,设加速时间为t,则:
得:
【问题一】分析无初速度的滑块在水平传送带上运动的时间.
A
B
V
【讨论二】传送带“刚够长”(物体到B时,速度刚好等于传送带的速度)
G
f
N
物体从A运动到B一直做匀加速,设加速时间为t,则:
得:
得:
【问题一】分析无初速度的滑块在水平传送带上运动的时间.
A
B
V
【讨论三】传送带“足够长”(物体到B前,速度等于传送带的速度,之后由于不再受摩擦力而做匀速运动)
G
f
N
物体做匀加速时间为:
G
N
物体做匀加速位移为:
物体做匀速时间为:
物体从A到B的总时间为:
得:
【结论】无初速度的滑块在水平传送带上的运动的时间
传送带刚够长
v0
v0
传送带 长度
滑块在传送带上的运动情景
滑块运动的时间
传送带不够长
v0
v
传送带足够长
v0
v0
得:
得:
【例1】如图所示,足够长的水平传送带以=2m/s的速度匀速运行。t=0时,在最左端轻放一质量为m的小滑块,t=2s时,传送带突然制动停下。已知滑块与传送带之间的动摩擦因数μ=0.2。下列关于滑块相对地面运动的v-t图像正确的是( )
D
【例2】物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下,则:( )
A. 物块将仍落在Q点
B. 物块将会落在Q点的左边
C. 物块将会落在Q点的右边
D. 物块有可能落不到地面上
P
Q
A
【例3】
B
1.概念:一个物体在另一个物体上发生相对滑动,两者之间有相对运动。问题涉及两个物体、多个过程,两物体的运动时间、速度、位移间有一定的关系。
2.模型的特点:
滑块(视为质点)置于木板上,滑块和木板均相对地面运动,且滑块和木板在摩擦力的相互作用下发生相对滑动。
专题六、板块模型(滑块—木板模型)
x1
模型特点
涉及两个发生相对滑动的物体.
两种位移关系
滑块由滑板的一端运动到另一端的过程中
若滑块和滑板同向运动,位移之差等于板长;
若滑块和滑板相向运动,位移之和等于板长.
设板长为L,滑块位移x1,滑板位移x2
同向运动时:
相向运动时:
x1
x2
L=x1-x2
L=x1+x2
x2
运动演示
易错辨析
同向运动两种类型:
【例1】如图所示,长为L=2m、质量为M=8kg的木板,放在水平地面上,木板向右运动的速度v0=6m/s时,在木板最前端轻放一个大小不计、质量为m=2kg的小物块。木板与地面、物块与木板间的动摩擦因数均为μ=0.2,g=10m/s2。求:
(1)物块的加速度大小a1;
(2)木板的加速度大小a2
(3)物块滑离木板时的时间t。
【例题2】如图所示,物块A、木板B的质量均为m=10kg,不计A的大小,B板长L=3m。开始时A、B均静止。现使A以某一水平初速度从B的最左端开始运动。已知A与B、B与水平面之间的动摩擦因数分别为μ1=0.3和μ2=0.1, g取10 m/s2。
(1)若物块A刚好没有从B上滑下来,则A的初速度多大
(2)若把木板B放在光滑水平面上,让A仍以(1)问中的初速度从B的最左端开始运动,则A能否与B脱离 最终A和B的速度各是多大
