2023-2024学年初中数学人教版九年级下册28.1.1 锐角三角函数 第1课时 正弦 课件(共16张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册28.1.1 锐角三角函数 第1课时 正弦 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 304.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
第二十八章 锐角三角函数
28.1.1 锐角三角函数
第1课时 正弦
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. 理解并掌握锐角正弦的定义,知道当直角三角形的锐角固定时,它的对边与斜边的比值都固定 (即正弦值不变).
2. 能根据正弦的概念进行相关计算.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.直角三角形中一个锐角的对边与斜边之比和这个锐角的关系
规 律:在 三角形中,当锐角A的度数一定时,不管三角形
的大小如何,∠A的对边与斜边的比都是一个 .
2.锐角的正弦定义
正 弦:在Rt△ABC中,∠C=90°,把锐角A的 与 的比
叫做∠A的正弦,记作 ,即sin A= .
直角
固定值
对边
斜边
sin A
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
B
C
c
a
b
对边
斜边
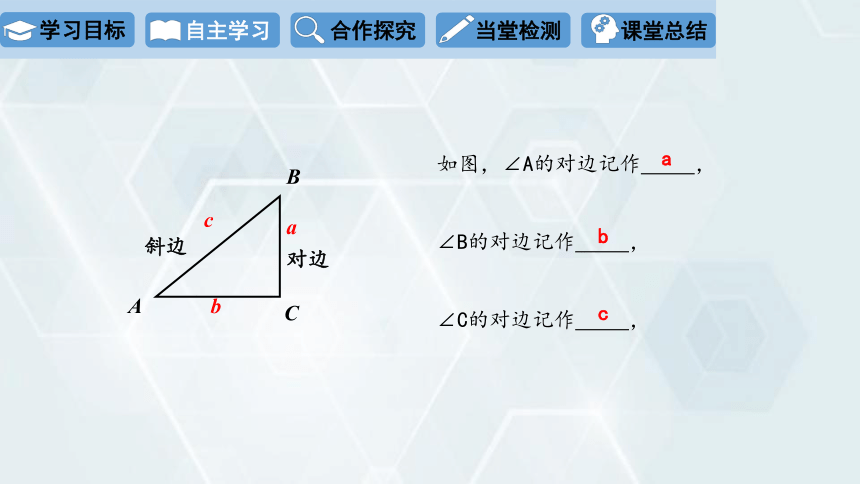
如图,∠A的对边记作 ,
∠B的对边记作 ,
∠C的对边记作 ,
a
b
c
合作探究
当堂检测
学习目标
课堂总结
自主学习
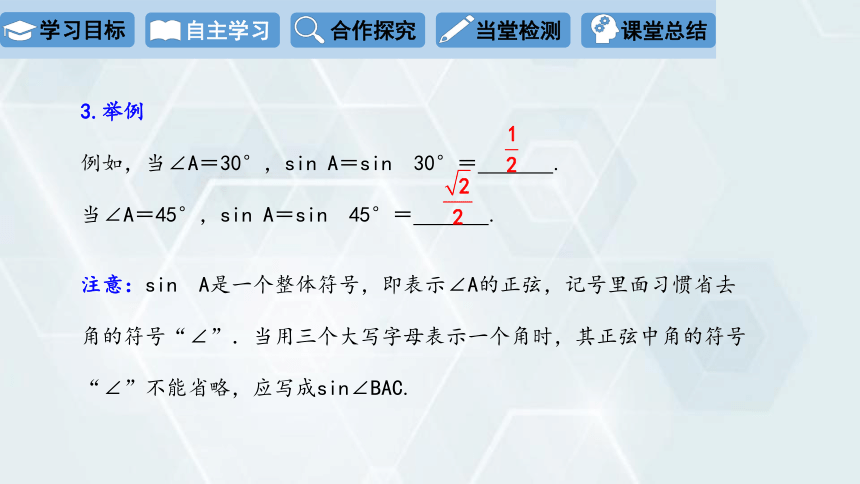
3.举例
例如,当∠A=30°,sin A=sin 30°= .
当∠A=45°,sin A=sin 45°= .
注意:sin A是一个整体符号,即表示∠A的正弦,记号里面习惯省去
角的符号“∠”.当用三个大写字母表示一个角时,其正弦中角的符号
“∠”不能省略,应写成sin∠BAC.
合作探究
当堂检测
学习目标
课堂总结
自主学习
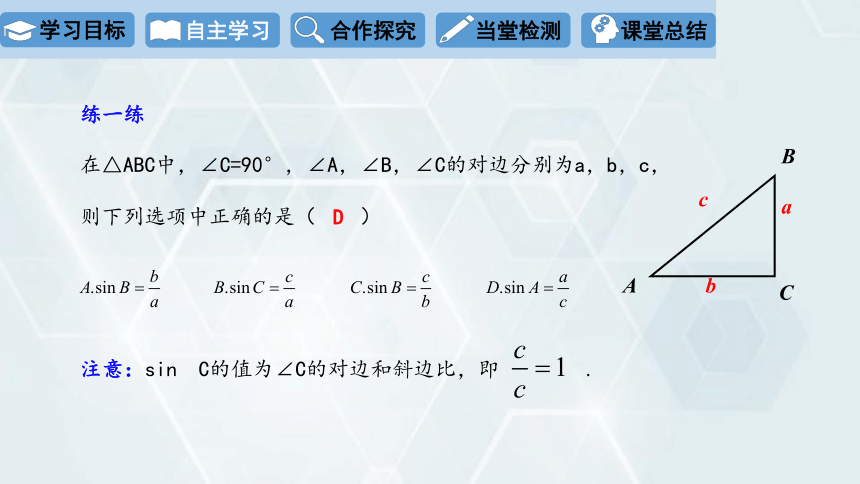
练一练
在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,
则下列选项中正确的是( )
D
A
B
C
c
a
b
注意:sin C的值为∠C的对边和斜边比,即 .
合作探究
当堂检测
学习目标
课堂总结
自主学习
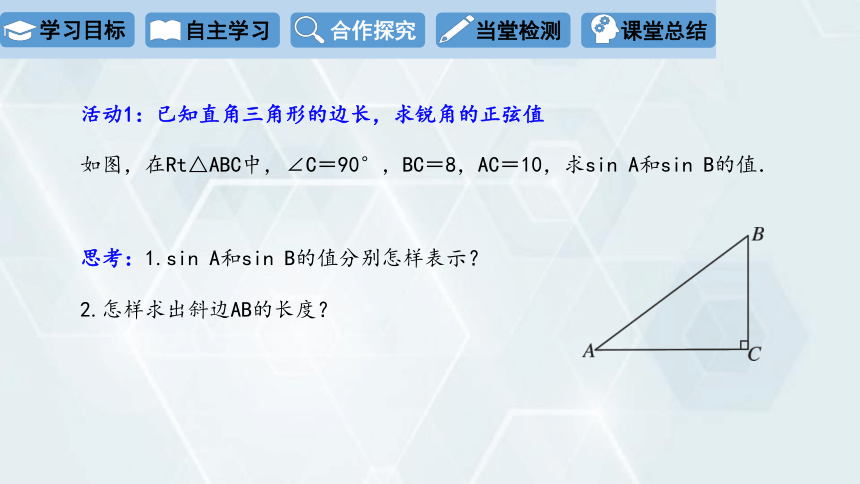
活动1:已知直角三角形的边长,求锐角的正弦值
如图,在Rt△ABC中,∠C=90°,BC=8,AC=10,求sin A和sin B的值.
思考:1.sin A和sin B的值分别怎样表示?
2.怎样求出斜边AB的长度?
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
┐
A
B
C
如图,在Rt△ABC中,∠C = 90°,AC = 12,
AB=13;则sinA的值为 .
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:已知锐角的正弦值,求直角三角形的边长
在△ABC中,∠C=90°,BC=6 cm,sin A= ,求AB,AC的长.
思考:1.AB的长与题中已知量有什么关系?
2.求出AB长后,AC的长如何求出?
合作探究
当堂检测
学习目标
课堂总结
自主学习
点悟:解这类题时,往往先由正弦定义及勾股定理得到直角三角形边与
边之间的关系,再综合这些关系求出直角三角形的边长.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,求BC的长.
解:在Rt△ABC中,
∴ BC=200×0.6=120.
A
B
C
即
合作探究
当堂检测
学习目标
课堂总结
自主学习
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
B
C
c
a
b
对边
斜边
锐角的正弦定义
在Rt△ABC中,∠C=90°,把锐角A的对边与斜边的比
叫做∠A的正弦,记作sin A.
sin A=
注意:sin A是一个整体符号,即表示∠A的正弦,记号里面习惯省去
角的符号“∠”.当用三个大写字母表示一个角时,其正弦中角的符号
“∠”不能省略,应写成sin∠BAC.
第二十八章 锐角三角函数
28.1.1 锐角三角函数
第1课时 正弦
合作探究
当堂检测
学习目标
课堂总结
自主学习
1. 理解并掌握锐角正弦的定义,知道当直角三角形的锐角固定时,它的对边与斜边的比值都固定 (即正弦值不变).
2. 能根据正弦的概念进行相关计算.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.直角三角形中一个锐角的对边与斜边之比和这个锐角的关系
规 律:在 三角形中,当锐角A的度数一定时,不管三角形
的大小如何,∠A的对边与斜边的比都是一个 .
2.锐角的正弦定义
正 弦:在Rt△ABC中,∠C=90°,把锐角A的 与 的比
叫做∠A的正弦,记作 ,即sin A= .
直角
固定值
对边
斜边
sin A
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
B
C
c
a
b
对边
斜边
如图,∠A的对边记作 ,
∠B的对边记作 ,
∠C的对边记作 ,
a
b
c
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.举例
例如,当∠A=30°,sin A=sin 30°= .
当∠A=45°,sin A=sin 45°= .
注意:sin A是一个整体符号,即表示∠A的正弦,记号里面习惯省去
角的符号“∠”.当用三个大写字母表示一个角时,其正弦中角的符号
“∠”不能省略,应写成sin∠BAC.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,
则下列选项中正确的是( )
D
A
B
C
c
a
b
注意:sin C的值为∠C的对边和斜边比,即 .
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1:已知直角三角形的边长,求锐角的正弦值
如图,在Rt△ABC中,∠C=90°,BC=8,AC=10,求sin A和sin B的值.
思考:1.sin A和sin B的值分别怎样表示?
2.怎样求出斜边AB的长度?
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
┐
A
B
C
如图,在Rt△ABC中,∠C = 90°,AC = 12,
AB=13;则sinA的值为 .
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:已知锐角的正弦值,求直角三角形的边长
在△ABC中,∠C=90°,BC=6 cm,sin A= ,求AB,AC的长.
思考:1.AB的长与题中已知量有什么关系?
2.求出AB长后,AC的长如何求出?
合作探究
当堂检测
学习目标
课堂总结
自主学习
点悟:解这类题时,往往先由正弦定义及勾股定理得到直角三角形边与
边之间的关系,再综合这些关系求出直角三角形的边长.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,求BC的长.
解:在Rt△ABC中,
∴ BC=200×0.6=120.
A
B
C
即
合作探究
当堂检测
学习目标
课堂总结
自主学习
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
B
C
c
a
b
对边
斜边
锐角的正弦定义
在Rt△ABC中,∠C=90°,把锐角A的对边与斜边的比
叫做∠A的正弦,记作sin A.
sin A=
注意:sin A是一个整体符号,即表示∠A的正弦,记号里面习惯省去
角的符号“∠”.当用三个大写字母表示一个角时,其正弦中角的符号
“∠”不能省略,应写成sin∠BAC.
