2023-2024学年初中数学人教版九年级下册28.2.1 解直角三角形 课件(共16张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册28.2.1 解直角三角形 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 724.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 08:45:49 | ||
图片预览






文档简介
(共16张PPT)
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.1 解直角三角形
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.进一步巩固锐角三角函数的计算.
2.理解直角三角形中的五个元素之间的联系. (重点)
3.学会解直角三角形.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
复习回顾
A
C
B
c
b
a
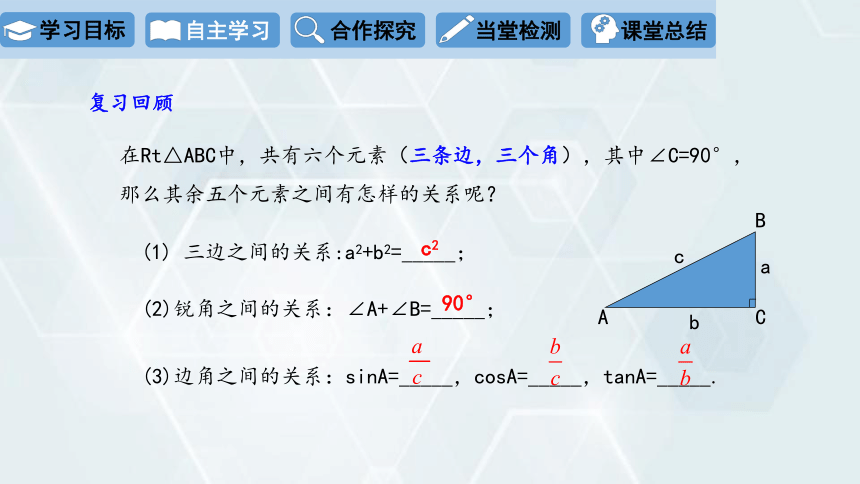
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
合作探究
当堂检测
学习目标
课堂总结
自主学习
在一个直角三角形中,除直角外有5个元素(3条边、2个锐角),要至少知道其中的几个元素就可以求出其余的元素?
如果知道的2个元素都是角,不能求解.因为此时的直角三角形有无数多个.
如果已知2个元素,且至少有一个元素是边就可以了.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:已知两边解直角三角形
问题提出:如果已知Rt△ABC中两边的长,你能求出这个三角形其他的元素吗?
情境:如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.
A
B
C
问题探究:
1.在直角三角形内,已知两边,可用 求出第三边;
勾股定理
2.求出第三边之后,根据前面所学利用科学计算器由三角函数值求角度便能得出三个内角度数(一般题目设置求出的会是30°,45°和60°的特殊角)
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
解:在Rt△ABC中,a2+b2=c2,
在Rt△ABC中,
A
B
C
小结:在直角三角形中,已知两边的长度能够求出其他元素
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
解:在Rt△ABC 中
∴∠B=60°
∴∠A=30°
1.在Rt△ABC中,∠A, ∠B, ∠C相对应的边分别是a,b,c,其中a= ,b= ,请求出直角三角形的其他元素(角度精确到1°)
∵∠C=90°,
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:已知一边及一锐角解直角三角形
问题提出:如果已知Rt△ABC中一边及一锐角,你能求出这个三角形其他的元素吗?
情境:在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°,求这个直角三角形的其他元素(边长精确到1).
A
B
C
b
30
c
a
25°
问题探究:
1.首先利用 思想,画出草图;
数形结合
2.直角三角形内隐含条件是∠C= ,结合题目中∠B=25°,得出∠A= ,最后结合三角函数得出其余两边长,必要时需借助计算器!
90°
65°
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
解:
在Rt△ABC中,∠C=90°,∠B=25°,
∴∠A=65°.
A
B
C
b
30
c
a
25°
小结:在直角三角形中,已知一边及一锐角亦能够求出其他元素
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
2.如图,在Rt△ABC中,∠C=90°,∠A=30°,a=5,求∠B,b,c.
解:根据题意得:∠B=60°,且tanB=
∴b=a·tanB=5tan60°=
∵sinA=
∴c=
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
揭示概念:在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
(3)三角函数:正切、正弦和余弦
(4)三角形面积公式
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB= ,则AC的长为( )
A.3 B.3.75 C.4.8 D.5
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 30 , b = 20 ;
解:根据勾股定理得
A
B
C
b=20
a=30
c
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2) ∠B=72°,c = 14.
A
B
C
b
a
c=14
解:
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,工地上有一V形槽(AC=BC),测得它的上口宽20mm,深19.2mm,求V形角(∠ACB)的度数 。
解:如图CD⊥AB于D点,
∵ AC=BC
∴ AD=0.5AB=10
∠ACD=0.5∠ACB
又 CD=19.2
∴ ∠ACD=27.74°
∴ ∠ACB=55.48°
合作探究
当堂检测
学习目标
课堂总结
自主学习
解直角三角形
依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
概念:在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
(3)三角函数:正切、正弦和余弦
(4)三角形面积公式
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.1 解直角三角形
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.进一步巩固锐角三角函数的计算.
2.理解直角三角形中的五个元素之间的联系. (重点)
3.学会解直角三角形.(难点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
复习回顾
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
合作探究
当堂检测
学习目标
课堂总结
自主学习
在一个直角三角形中,除直角外有5个元素(3条边、2个锐角),要至少知道其中的几个元素就可以求出其余的元素?
如果知道的2个元素都是角,不能求解.因为此时的直角三角形有无数多个.
如果已知2个元素,且至少有一个元素是边就可以了.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:已知两边解直角三角形
问题提出:如果已知Rt△ABC中两边的长,你能求出这个三角形其他的元素吗?
情境:如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.
A
B
C
问题探究:
1.在直角三角形内,已知两边,可用 求出第三边;
勾股定理
2.求出第三边之后,根据前面所学利用科学计算器由三角函数值求角度便能得出三个内角度数(一般题目设置求出的会是30°,45°和60°的特殊角)
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
解:在Rt△ABC中,a2+b2=c2,
在Rt△ABC中,
A
B
C
小结:在直角三角形中,已知两边的长度能够求出其他元素
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
解:在Rt△ABC 中
∴∠B=60°
∴∠A=30°
1.在Rt△ABC中,∠A, ∠B, ∠C相对应的边分别是a,b,c,其中a= ,b= ,请求出直角三角形的其他元素(角度精确到1°)
∵∠C=90°,
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:已知一边及一锐角解直角三角形
问题提出:如果已知Rt△ABC中一边及一锐角,你能求出这个三角形其他的元素吗?
情境:在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°,求这个直角三角形的其他元素(边长精确到1).
A
B
C
b
30
c
a
25°
问题探究:
1.首先利用 思想,画出草图;
数形结合
2.直角三角形内隐含条件是∠C= ,结合题目中∠B=25°,得出∠A= ,最后结合三角函数得出其余两边长,必要时需借助计算器!
90°
65°
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
解:
在Rt△ABC中,∠C=90°,∠B=25°,
∴∠A=65°.
A
B
C
b
30
c
a
25°
小结:在直角三角形中,已知一边及一锐角亦能够求出其他元素
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
2.如图,在Rt△ABC中,∠C=90°,∠A=30°,a=5,求∠B,b,c.
解:根据题意得:∠B=60°,且tanB=
∴b=a·tanB=5tan60°=
∵sinA=
∴c=
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
揭示概念:在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
(3)三角函数:正切、正弦和余弦
(4)三角形面积公式
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB= ,则AC的长为( )
A.3 B.3.75 C.4.8 D.5
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 30 , b = 20 ;
解:根据勾股定理得
A
B
C
b=20
a=30
c
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2) ∠B=72°,c = 14.
A
B
C
b
a
c=14
解:
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,工地上有一V形槽(AC=BC),测得它的上口宽20mm,深19.2mm,求V形角(∠ACB)的度数 。
解:如图CD⊥AB于D点,
∵ AC=BC
∴ AD=0.5AB=10
∠ACD=0.5∠ACB
又 CD=19.2
∴ ∠ACD=27.74°
∴ ∠ACB=55.48°
合作探究
当堂检测
学习目标
课堂总结
自主学习
解直角三角形
依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
概念:在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
(3)三角函数:正切、正弦和余弦
(4)三角形面积公式
