2023-2024学年初中数学人教版九年级下册28.2.2 应用举例 第1课时 仰角、俯角问题 课件(共19张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册28.2.2 应用举例 第1课时 仰角、俯角问题 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 428.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 08:46:54 | ||
图片预览






文档简介
(共19张PPT)
第二十八章 锐角三角函数
28.2.2 解直角三角形的应用举例
第1课时 仰角、俯角问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.巩固解直角三角形的相关知识.
2.能从实际问题中构造直角三角形,从而把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题,如与仰角、俯角等有关的实际问题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
小颖的教室在教学楼的二楼,一天,她站在教室的窗台前看操场上的旗杆,
心想:站在二楼上可以利用解直角三角形测得旗杆的高吗?她望着旗杆顶端
和旗杆底部,可以测得视线与水平视线之间的夹角各一个,但是,这两个角
怎样命名区别呢?如图,∠CAE,∠DAE在测量中分别叫什么角呢?
合作探究
当堂检测
学习目标
课堂总结
自主学习
方 法:(1)圆的切线与 的半径垂直,常通过连圆心与切点构造
直角三角形来解决实际问题,如从飞船上能直接看到地球上最远的点应是视线
与地面 的点,故应作出过 的半径,它与切线 ,从而
构造出直角三角形.
(2)利用直径所对的圆周角是直角构造直角三角形.
1.解直角三角形在圆中的应用
过切点
相切时
切点
垂直
合作探究
当堂检测
学习目标
课堂总结
自主学习
仰 角:在视线与水平线所成的角中,视线在水平线 的角是仰角.
俯 角:在视线与水平线所成的角中,视线在水平线 的角是俯角.
方 法:解决有关仰角、俯角的实际问题时,常通过解视线与水平线构成
的双直角三角形,得到实际问题的结果.
2.仰角、俯角
上方
下方
合作探究
当堂检测
学习目标
课堂总结
自主学习
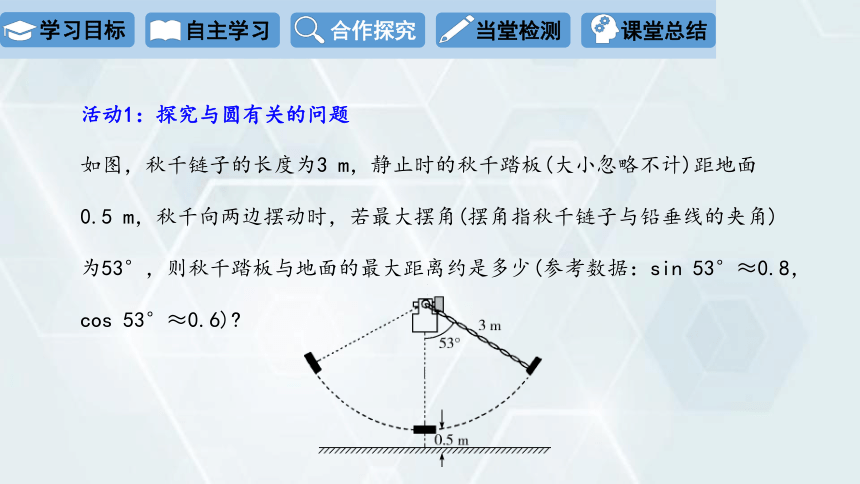
活动1:探究与圆有关的问题
如图,秋千链子的长度为3 m,静止时的秋千踏板(大小忽略不计)距地面
0.5 m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)
为53°,则秋千踏板与地面的最大距离约是多少(参考数据:sin 53°≈0.8,
cos 53°≈0.6)
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:如图,设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时
踏板位于B处,过点A,B的铅垂线分别为AD,BE,点D,E在地面上,过
点B作BC⊥AD于点C.
合作探究
当堂检测
学习目标
课堂总结
自主学习
在Rt△ABC中,∵AB=3 m,∠CAB=53°,
∴AC=AB·cos 53°≈1.8(m).
易证四边形CDEB是矩形,
∴BE=CD=AD-AC≈1.7(m),
∴秋千踏板与地面的最大距离约是1.7 m.
点悟:解决与圆有关的三角函数问题时,常通过作垂线构造直角三角形,
再利用垂径定理、勾股定理或三角函数来求解.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,⊙O的半径为4 cm,PA,PB是⊙O的两条切线,∠APB=60°,
则AP= cm.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:探究与仰角、俯角相关的测量与计算
小组讨论:如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,
AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,
求山高.(结果保留根号)请与同伴交流你是怎么想的 准备怎么去做
问题探究:
1.求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解
2.运用 思想,先把AC看成已知,用含AC的代数式表示BC和DC,
由BD=1000m建立关于AC的方程,从而求得AC.
方程
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
问题解决:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200米,点C在BD上,则树高AB等于 (根号保留).
合作探究
当堂检测
学习目标
课堂总结
自主学习
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.仰角与俯角
铅直线
水平线
视线
视线
仰角
俯角
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.用三角函数知识解决实际问题的一般步骤:
(1)通过读题把已知转化为数学图形;
(2)找出直角三角形和已知、未知元素;
(3)选择合适的锐角三角函数求未知数;
(4)解题.
第二十八章 锐角三角函数
28.2.2 解直角三角形的应用举例
第1课时 仰角、俯角问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.巩固解直角三角形的相关知识.
2.能从实际问题中构造直角三角形,从而把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题,如与仰角、俯角等有关的实际问题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
小颖的教室在教学楼的二楼,一天,她站在教室的窗台前看操场上的旗杆,
心想:站在二楼上可以利用解直角三角形测得旗杆的高吗?她望着旗杆顶端
和旗杆底部,可以测得视线与水平视线之间的夹角各一个,但是,这两个角
怎样命名区别呢?如图,∠CAE,∠DAE在测量中分别叫什么角呢?
合作探究
当堂检测
学习目标
课堂总结
自主学习
方 法:(1)圆的切线与 的半径垂直,常通过连圆心与切点构造
直角三角形来解决实际问题,如从飞船上能直接看到地球上最远的点应是视线
与地面 的点,故应作出过 的半径,它与切线 ,从而
构造出直角三角形.
(2)利用直径所对的圆周角是直角构造直角三角形.
1.解直角三角形在圆中的应用
过切点
相切时
切点
垂直
合作探究
当堂检测
学习目标
课堂总结
自主学习
仰 角:在视线与水平线所成的角中,视线在水平线 的角是仰角.
俯 角:在视线与水平线所成的角中,视线在水平线 的角是俯角.
方 法:解决有关仰角、俯角的实际问题时,常通过解视线与水平线构成
的双直角三角形,得到实际问题的结果.
2.仰角、俯角
上方
下方
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动1:探究与圆有关的问题
如图,秋千链子的长度为3 m,静止时的秋千踏板(大小忽略不计)距地面
0.5 m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)
为53°,则秋千踏板与地面的最大距离约是多少(参考数据:sin 53°≈0.8,
cos 53°≈0.6)
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:如图,设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时
踏板位于B处,过点A,B的铅垂线分别为AD,BE,点D,E在地面上,过
点B作BC⊥AD于点C.
合作探究
当堂检测
学习目标
课堂总结
自主学习
在Rt△ABC中,∵AB=3 m,∠CAB=53°,
∴AC=AB·cos 53°≈1.8(m).
易证四边形CDEB是矩形,
∴BE=CD=AD-AC≈1.7(m),
∴秋千踏板与地面的最大距离约是1.7 m.
点悟:解决与圆有关的三角函数问题时,常通过作垂线构造直角三角形,
再利用垂径定理、勾股定理或三角函数来求解.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,⊙O的半径为4 cm,PA,PB是⊙O的两条切线,∠APB=60°,
则AP= cm.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:探究与仰角、俯角相关的测量与计算
小组讨论:如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,
AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,
求山高.(结果保留根号)请与同伴交流你是怎么想的 准备怎么去做
问题探究:
1.求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解
2.运用 思想,先把AC看成已知,用含AC的代数式表示BC和DC,
由BD=1000m建立关于AC的方程,从而求得AC.
方程
合作探究
当堂检测
学习目标
课堂总结
自主学习
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
问题解决:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200米,点C在BD上,则树高AB等于 (根号保留).
合作探究
当堂检测
学习目标
课堂总结
自主学习
D
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.仰角与俯角
铅直线
水平线
视线
视线
仰角
俯角
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.用三角函数知识解决实际问题的一般步骤:
(1)通过读题把已知转化为数学图形;
(2)找出直角三角形和已知、未知元素;
(3)选择合适的锐角三角函数求未知数;
(4)解题.
