2023-2024学年初中数学人教版九年级下册第二十八章 锐角三角函数复习课 课件(共23张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版九年级下册第二十八章 锐角三角函数复习课 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 447.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 08:54:42 | ||
图片预览







文档简介
(共23张PPT)
复习课
第二十八章 锐角三角函数
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解锐角三角函数的定义,掌握特殊角的三角函数值,并进行
相关计算.
2.理解直角三角形中的五个元素之间的联系,掌握解直角三角形
的方法.
3.掌握数形结合思想、转化思想、方程思想方法,会用解直角三角形的有关知识解决某些实际问题.
考点探究
学习目标
课堂总结
知识梳理
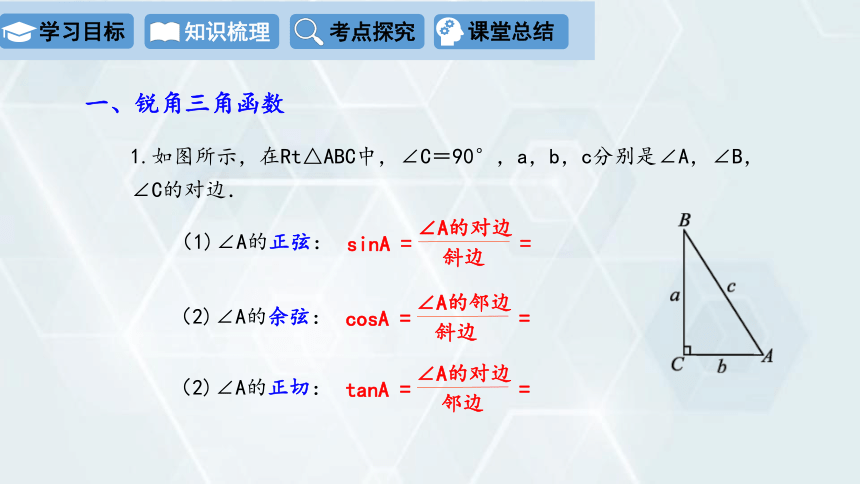
一、锐角三角函数
1.如图所示,在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)∠A的正弦:
sinA = =
∠A的对边
斜边
(2)∠A的余弦:
cosA = =
∠A的邻边
斜边
(2)∠A的正切:
tanA = =
∠A的对边
邻边
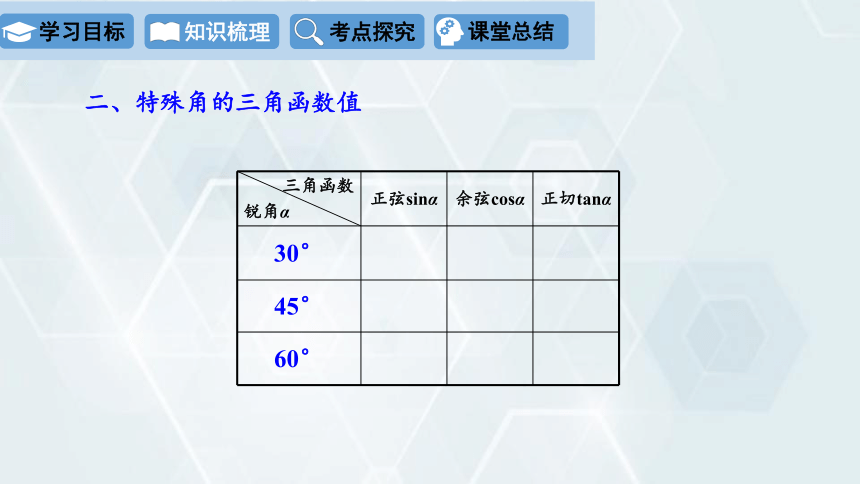
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
二、特殊角的三角函数值
考点探究
学习目标
课堂总结
知识梳理
三、锐角三角函数的计算
1.利用计算器求三角函数值.
第二步:输入角度值,
屏幕显示结果.
(有的计算器是先输入角度再按函数名称键)
第一步:按计算器 、 、 键,
sin
tan
cos
考点探究
学习目标
课堂总结
知识梳理
2.利用计算器求锐角的度数.
第二步:然后输入函数值
屏幕显示答案(按实际需要进行精确)
还可以利用 键,进一步得到角的度数.
°'″
第一步:按计算器 、 、 键,
sin
cos
tan
SHIFT
考点探究
学习目标
课堂总结
知识梳理
四、解直角三角形
2.依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
1.概念:在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
(3)三角函数:正切、正弦和余弦
(4)三角形面积公式
考点探究
学习目标
课堂总结
知识梳理
3.直角三角形可解的条件和解法:
条件:解直角三角形时知道其中的2个元素(至少有一个是边),就可以求出其余的3个未知元素.
解法:①一边一锐角,先由两锐角互余关系求出另一锐角;
②知两边:先用勾股定理求另一边,再用边角关系求锐角;
③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.
考点探究
学习目标
课堂总结
知识梳理
五、三角形函数的应用
1.仰角和俯角
2.坡角
3.方位角
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(数形结合);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
考点探究
学习目标
课堂总结
知识梳理
考点一:锐角三角函数
考点探究
学习目标
课堂总结
知识梳理
例1.如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sin B的值为 ( )
A. B. C. D.
解:如图,连接CD,
由勾股定理得CD= ,BC= ,BD=2 ,
则CD2+BD2=BC2,∴∠CDB=90°,
∴sin B= .
D
D
构造直角三角形十分关键哦!
考点探究
学习目标
课堂总结
知识梳理
当堂检测
1.如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的格点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin ∠BAD的值为( )
A. B. C. D.2
A
考点二:特殊角的三角函数值
考点探究
学习目标
课堂总结
知识梳理
例2.已知α,β均为锐角,且满足 =0,求α+β的值.
解:
∴α=30°,β=45°,∴α+β=30°+45°=75°.
找到题目条件与三角函数之间的联系,先化简再求值!
考点探究
学习目标
课堂总结
知识梳理
当堂检测
2.在△ABC中,三边之比为BC∶AC∶AB=1∶ ∶2,则sin A+tan A等于( )
A. B. C. D.
3.在△ABC中,∠A,∠B为锐角,且有|tan B- |+(2sin A- )2=0,则△ABC的形状是 .
等边三角形
A
考点探究
学习目标
课堂总结
知识梳理
当堂检测
4.计算:
解:原式=
考点三:解直角三角形
考点探究
学习目标
课堂总结
知识梳理
例3.如图,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,
求:(1)DC的长;(2)sinB的值.
【分析】题中给出了两个直角三角形,DC和sinB可分别在Rt△ACD和ABC中求得,由AD=BC,图中CD=BC-BD,由此可列方程求出CD.
A
B
C
D
考点探究
学习目标
课堂总结
知识梳理
解:(1)设CD=x,在Rt△ACD中,cos∠ADC= ,
又 BC-CD=BD,
解得x=6,
∴CD=6.
A
B
C
D
∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求:(1)DC的长
考点探究
学习目标
课堂总结
知识梳理
∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求sinB的值.
A
B
C
D
解:(2)BC=BD+CD=4+6=10=AD
在Rt△ACD中
在Rt△ABC中
考点探究
学习目标
课堂总结
知识梳理
当堂检测
5.如图所示,把一张长方形卡片ABCD放在每格宽度为12 mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.( 结果精确到1 mm,参考数据:sin 36°≈0.60,cos 36°≈0.80,tan 36°≈0.75 )
考点探究
学习目标
课堂总结
知识梳理
当堂检测
解:作BE⊥l于点E,DF⊥l于点F.
∵α+∠DAF=180°-∠BAD=90°,∠ADF+∠DAF=90°,
∴∠ADF=α=36°.
根据题意得BE=24 mm,DF=48 mm.
在Rt△ABE中,sin α= ,∴AB= ≈40 mm.
在Rt△ADF中,cos ∠ADF= ,
∴AD= ≈60 mm.
∴长方形卡片的周长为2×( 40+60 )=200 mm.
E
F
考点四:三角函数的实际应用
考点探究
学习目标
课堂总结
知识梳理
例4.如图,在一次数学课外实践活动中,要求测教学楼AB的高度.小刚在D处用高1.5 m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40 m到达EF,又测得教学楼顶端A的仰角为60°.求这幢教学楼AB的高度
【分析】 设CF与AB交于点G,在Rt△AFG中,用AG表示出FG,在Rt△ACG中,用AG表示出CG,然后根据CG-FG=40,可求AG.
G
考点探究
学习目标
课堂总结
知识梳理
解:设CF与AB交于点G,在Rt△AFG中,
tan∠AFG= ,∴FG=
在Rt△ACG中,tan∠ACG= ,
又CG-FG=40,
∴AG= ,∴AB=
答:这幢教学楼AB的高度为
∴
G
考点探究
学习目标
课堂总结
知识梳理
当堂检测
6.如图,某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到旗杆的距离(即CE的长)为8米,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45 °,则旗杆AB的高度是多少米
C
A
B
D
E
解:如图在Rt△ACE和Rt△BCE中
∠ACE=30°,EC=8米
∴tan∠ACE= ,tan∠ECB=
即:AE=8tan30°= (米)EB=8tan45°=8(米)
∴AE+EB=(8+ )米
锐角三角函数
直角三角函数的边角关系
解直角三角形
三角函数的计算
三角函数的应用
正弦(sinA)
余弦(cosA)
正切(tanA)
概念、依据、解法
利用科学计算器求值
仰角和俯角、坡角、
方位角
考点探究
学习目标
课堂总结
知识梳理
复习课
第二十八章 锐角三角函数
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解锐角三角函数的定义,掌握特殊角的三角函数值,并进行
相关计算.
2.理解直角三角形中的五个元素之间的联系,掌握解直角三角形
的方法.
3.掌握数形结合思想、转化思想、方程思想方法,会用解直角三角形的有关知识解决某些实际问题.
考点探究
学习目标
课堂总结
知识梳理
一、锐角三角函数
1.如图所示,在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)∠A的正弦:
sinA = =
∠A的对边
斜边
(2)∠A的余弦:
cosA = =
∠A的邻边
斜边
(2)∠A的正切:
tanA = =
∠A的对边
邻边
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
二、特殊角的三角函数值
考点探究
学习目标
课堂总结
知识梳理
三、锐角三角函数的计算
1.利用计算器求三角函数值.
第二步:输入角度值,
屏幕显示结果.
(有的计算器是先输入角度再按函数名称键)
第一步:按计算器 、 、 键,
sin
tan
cos
考点探究
学习目标
课堂总结
知识梳理
2.利用计算器求锐角的度数.
第二步:然后输入函数值
屏幕显示答案(按实际需要进行精确)
还可以利用 键,进一步得到角的度数.
°'″
第一步:按计算器 、 、 键,
sin
cos
tan
SHIFT
考点探究
学习目标
课堂总结
知识梳理
四、解直角三角形
2.依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
1.概念:在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
(3)三角函数:正切、正弦和余弦
(4)三角形面积公式
考点探究
学习目标
课堂总结
知识梳理
3.直角三角形可解的条件和解法:
条件:解直角三角形时知道其中的2个元素(至少有一个是边),就可以求出其余的3个未知元素.
解法:①一边一锐角,先由两锐角互余关系求出另一锐角;
②知两边:先用勾股定理求另一边,再用边角关系求锐角;
③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.
考点探究
学习目标
课堂总结
知识梳理
五、三角形函数的应用
1.仰角和俯角
2.坡角
3.方位角
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(数形结合);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
考点探究
学习目标
课堂总结
知识梳理
考点一:锐角三角函数
考点探究
学习目标
课堂总结
知识梳理
例1.如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sin B的值为 ( )
A. B. C. D.
解:如图,连接CD,
由勾股定理得CD= ,BC= ,BD=2 ,
则CD2+BD2=BC2,∴∠CDB=90°,
∴sin B= .
D
D
构造直角三角形十分关键哦!
考点探究
学习目标
课堂总结
知识梳理
当堂检测
1.如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的格点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin ∠BAD的值为( )
A. B. C. D.2
A
考点二:特殊角的三角函数值
考点探究
学习目标
课堂总结
知识梳理
例2.已知α,β均为锐角,且满足 =0,求α+β的值.
解:
∴α=30°,β=45°,∴α+β=30°+45°=75°.
找到题目条件与三角函数之间的联系,先化简再求值!
考点探究
学习目标
课堂总结
知识梳理
当堂检测
2.在△ABC中,三边之比为BC∶AC∶AB=1∶ ∶2,则sin A+tan A等于( )
A. B. C. D.
3.在△ABC中,∠A,∠B为锐角,且有|tan B- |+(2sin A- )2=0,则△ABC的形状是 .
等边三角形
A
考点探究
学习目标
课堂总结
知识梳理
当堂检测
4.计算:
解:原式=
考点三:解直角三角形
考点探究
学习目标
课堂总结
知识梳理
例3.如图,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,
求:(1)DC的长;(2)sinB的值.
【分析】题中给出了两个直角三角形,DC和sinB可分别在Rt△ACD和ABC中求得,由AD=BC,图中CD=BC-BD,由此可列方程求出CD.
A
B
C
D
考点探究
学习目标
课堂总结
知识梳理
解:(1)设CD=x,在Rt△ACD中,cos∠ADC= ,
又 BC-CD=BD,
解得x=6,
∴CD=6.
A
B
C
D
∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求:(1)DC的长
考点探究
学习目标
课堂总结
知识梳理
∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求sinB的值.
A
B
C
D
解:(2)BC=BD+CD=4+6=10=AD
在Rt△ACD中
在Rt△ABC中
考点探究
学习目标
课堂总结
知识梳理
当堂检测
5.如图所示,把一张长方形卡片ABCD放在每格宽度为12 mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.( 结果精确到1 mm,参考数据:sin 36°≈0.60,cos 36°≈0.80,tan 36°≈0.75 )
考点探究
学习目标
课堂总结
知识梳理
当堂检测
解:作BE⊥l于点E,DF⊥l于点F.
∵α+∠DAF=180°-∠BAD=90°,∠ADF+∠DAF=90°,
∴∠ADF=α=36°.
根据题意得BE=24 mm,DF=48 mm.
在Rt△ABE中,sin α= ,∴AB= ≈40 mm.
在Rt△ADF中,cos ∠ADF= ,
∴AD= ≈60 mm.
∴长方形卡片的周长为2×( 40+60 )=200 mm.
E
F
考点四:三角函数的实际应用
考点探究
学习目标
课堂总结
知识梳理
例4.如图,在一次数学课外实践活动中,要求测教学楼AB的高度.小刚在D处用高1.5 m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40 m到达EF,又测得教学楼顶端A的仰角为60°.求这幢教学楼AB的高度
【分析】 设CF与AB交于点G,在Rt△AFG中,用AG表示出FG,在Rt△ACG中,用AG表示出CG,然后根据CG-FG=40,可求AG.
G
考点探究
学习目标
课堂总结
知识梳理
解:设CF与AB交于点G,在Rt△AFG中,
tan∠AFG= ,∴FG=
在Rt△ACG中,tan∠ACG= ,
又CG-FG=40,
∴AG= ,∴AB=
答:这幢教学楼AB的高度为
∴
G
考点探究
学习目标
课堂总结
知识梳理
当堂检测
6.如图,某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到旗杆的距离(即CE的长)为8米,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45 °,则旗杆AB的高度是多少米
C
A
B
D
E
解:如图在Rt△ACE和Rt△BCE中
∠ACE=30°,EC=8米
∴tan∠ACE= ,tan∠ECB=
即:AE=8tan30°= (米)EB=8tan45°=8(米)
∴AE+EB=(8+ )米
锐角三角函数
直角三角函数的边角关系
解直角三角形
三角函数的计算
三角函数的应用
正弦(sinA)
余弦(cosA)
正切(tanA)
概念、依据、解法
利用科学计算器求值
仰角和俯角、坡角、
方位角
考点探究
学习目标
课堂总结
知识梳理
