第24章圆 章末复习课课件 (共64张PPT)人教版九年级数学上册
文档属性
| 名称 | 第24章圆 章末复习课课件 (共64张PPT)人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 09:00:37 | ||
图片预览









文档简介
(共64张PPT)
第24章 圆
章末复习课
与圆有关的性质
01
与圆有关的位置
02
与圆有关的计算
03
知识点
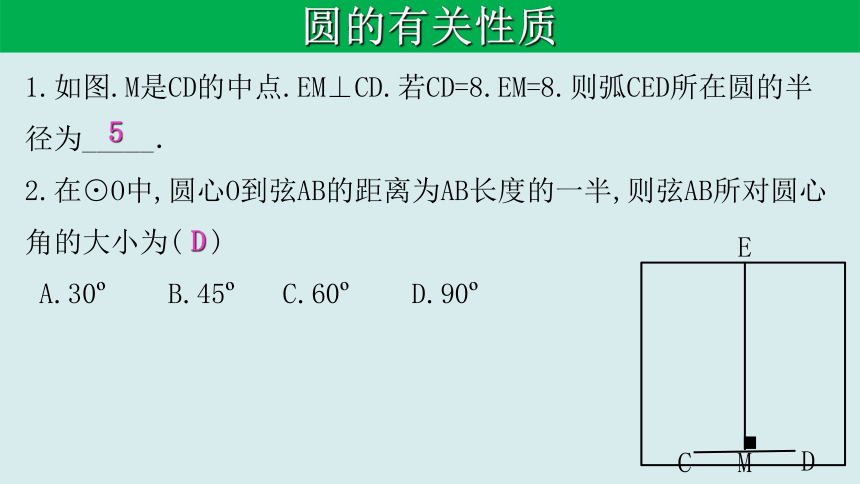
1.如图.M是CD的中点.EM⊥CD.若CD=8.EM=8.则弧CED所在圆的半径为_____.
2.在⊙O中,圆心O到弦AB的距离为AB长度的一半,则弦AB所对圆心角的大小为( )
A.30 B.45 C.60 D.90
圆的有关性质
D
E
M
D
C
5
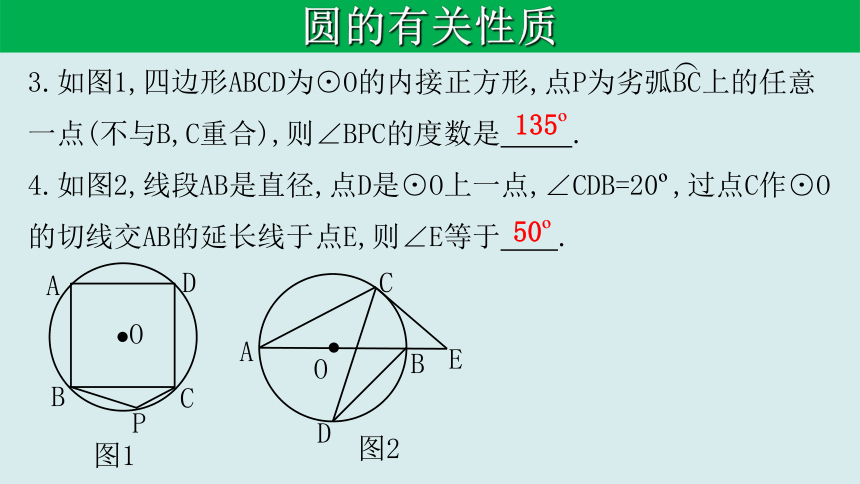
3.如图1,四边形ABCD为⊙O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是 .
4.如图2,线段AB是直径,点D是⊙O上一点,∠CDB=20 ,过点C作⊙O的切线交AB的延长线于点E,则∠E等于 .
(
135
C
D
B
A
P
O
图1
O
C
A
B
E
D
图2
50
圆的有关性质
基础练习
5.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:△CDE是等边三角形;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
圆的有关性质
A
B
C
D
P
O
图b
1.如图b,AB是⊙O的直径,且AB=2,C,D是同一半圆上的两点,并且AC与BD的度数分别是96 和36 ,动点P是AB上的任意一点,则PC+PD的最小值是 .
(
(
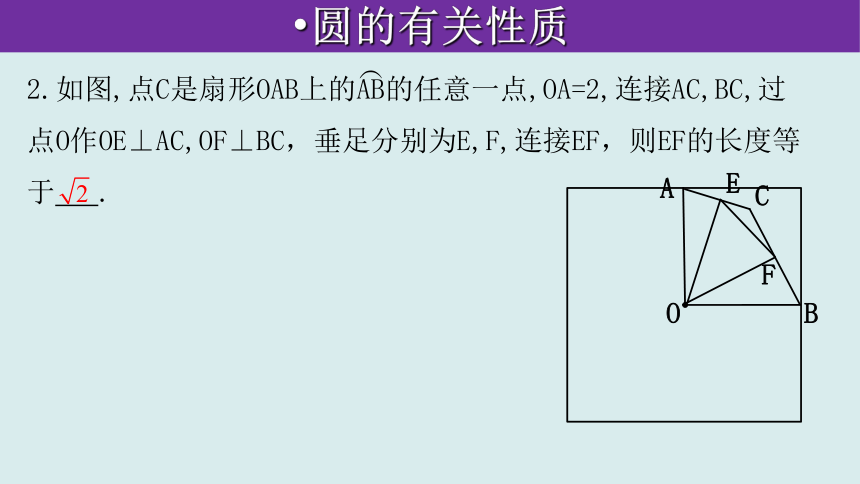
2.如图,点C是扇形OAB上的AB的任意一点,OA=2,连接AC,BC,过点O作OE⊥AC,OF⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
(
A
O
B
C
E
F
圆的有关性质
圆的有关性质
3.在⊙O中,弦AB所对的圆心角∠AOB=100 则弦AB所对的圆周角为__________.
4.如图,AB是⊙O的直径,弦BC=2,F是弦BC的中点,∠ABC=60 .若动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t(s)((0<t<3)连接EF,
当t= s时,△BEF是直角三角形.
50 或130
A
B
C
E
O
F
与圆有关的性质
01
与圆有关的位置
02
与圆有关的计算
03
知识点
1.☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )
A.点A在☉O内部 B.点A在☉O上
C.点A在☉O外部 D.点A不在☉O上
2.点O是△ABC的外心,若∠BOC=80 ,则∠BAC的度数为( )
A.40 B.100 C.40 或140 D.40 或100
3.点O是△ABC的内心,若∠BAC=70 ,则∠BOC=_____.
4.在△ABC,∠C=90 ,AC=6,BC=8,则△ABC的外接圆面积是_____.
与圆有关的位置关系
D
C
125
25π
与圆有关的位置关系
1.如图,直线AB,CD相交于点O,∠AOD=30 ,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么 秒钟后⊙P与直线CD相切.
A
B
D
C
P
P1
P2
E
4或8
思路点拨:根本题应分为两种情况:(1)⊙P在直线AB下面与直线CD相切;
(2)⊙P在直线AB上面与直线CD相切.
与圆有关的位置关系
2.已知:如图,PA,PB是⊙O的切线,A、B为切点,过 上的一点C作⊙O的切线,交PA于D,交PB于E.
(1)若∠P=70 ,求∠DOE的度数;
(2)若PA=4cm,求△PDE的周长.
P
C
D
E
B
A
(1)∠DOE=55°
(2)△PDE的周长=PD+PE+DE
=PD+AD+BE+PE=2PA=8(cm)
与圆有关的性质
01
与圆有关的位置
02
与圆有关的计算
03
知识点
1.如图的扇形是一个圆锥的侧面展开图,若∠AOB=120 ,AB的长为12πcm,则该圆锥的侧面积为_____cm2.
2.如图,点A,B,C在⊙O上,⊙O的半径为9,
AB的长为2π,则∠ACB的大小是_____.
3.用一个圆心角为120 ,半径为6的扇形
作一个圆锥的侧面,这个圆锥的底面圆
的半径是____.
考点4:与圆有关的计算
108π
20
2
︵
︵
考点4:与圆有关的计算
4.(1)一条弧所对的圆心角为135 ,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 .
(2)若一个正六边形的周长为24,则该正六边形的面积为_____.
5.如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120 ,则图中阴影部分的面积等于____.
40cm
12.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是____(结果保留π)
基础练习
考点4:与圆有关的计算
5.如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上,OA=1,∠AOC=120 ,∠1=∠2,则扇形OEF的面积
基础练习
6.将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,
则这个圆锥的高为( )
A
A
B
基础练习
8.如图,已知正六边形ABCDEF内接于半径为4的⊙O,则阴影部分的面积为________.
基础练习
10.如图,将弧长为6π,圆心角为120 的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘连部分忽略不计),则圆锥形纸帽的高是____.
11.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长为____.
4π
基础练习
19.如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60 ,过点D作⊙O的切线CD交AB的延长线于点C,E为弧AD的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
考点4:与圆有关的计算
1.如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
C
A
E
F
D
C
B
考点4:与圆有关的计算
2.如下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形是扇形OAB,经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm,求
(1)扇形OAB的圆心角;
(2)这个纸杯的表面积.
(面积计算结果保留用π).
A
B
C
D
O
E
F
6cm
4cm
8cm
S纸杯表=44π(cm2).
补 充 练 习
OPTION
1.如图,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度)=那么y与点P运动的时间x(单位:秒)的关系图是( )
B
拓展提高
2.如图,根据天气预报,某台风中心位于A市正东方向300km的点O处,正以20km/h的速度向北偏西60 方向移动,距离台风中心250
km范围内都会受到影响,若台风移动的速度和方向不变,则A市受台风影响持续的时间是( )
A.10h B.20h C.30h D. 40h
B
拓展提高
北
东
A
O
M
60°
(
3.一电工沿着如图所示的梯子NL往上爬,当他爬到中点M处时,由于地面太滑,梯子沿墙面与地面滑下,设点M的坐标为(x,y)(x>0),则y与x之间的函数关系用图象表示大致是( )
C
拓展提高
L
M
N
L
M
N
y
O
x
A
y
O
x
B
y
O
x
C
y
O
x
D
4.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则EF:GH的值是( )
C
拓展提高
5.如图,点P是圆上一动点,弦AB= cm,PC平分∠APB,∠BAC=30 .当∠PAC=_ 时,四边形PACB有最大面积,此时最大面积是_ cm2
P
B
A
C
90
拓展提高
1.在⊙O中,直径AB=6,BC是弦,∠ABC=30 ,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
综合练习
A
Q
P
C
B
O
图1
A
Q
P
C
B
O
图2
综合练习
1.如图,在Rt△AOB中,OB= ,∠A=30 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),求线段PQ长度的最小值。
A
P
Q
O
B
2.如图,△ABC是⊙O的内接正三角形,P为弧BC上的一动点。
(1)求证:PA平分∠BPC.
(2)求证:PA=PB+PC.
A
P
O
C
B
D
综合练习
综合练习
3.已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接DE.
(1)若AD=DB,OC=5,求切线AC的长;
(2)求证:ED是⊙O的切线.
10
B
D
E
O
C
A
4.如图,⊙O的直径AB=4,∠ABC=30 ,BC交⊙O于D,D是BC的中点.
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,
求证:直线DE是⊙O的切线.
A
E
D
C
O
B
综合练习
5.已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D,∠DAC=20
(1)如图1,当直线l与⊙O相切于点C时,求∠BAC的大小,
(2)如图2,当直线l与⊙O相交于点C,E时,求∠BAE的大小.
O
l
C
A
D
B
如图1
O
l
C
A
D
B
E
如图2
(1)∠BAC=∠DAC=20
(2)∠BAE=∠DAC=20
综合练习
6.大练P568.如图,AD为△ABC外接圆的直径,AD⊥BC于点F,∠ABC的平分线交AD于点E,连接BD、CD.
(1)求证:BD=CD
(2)试判断B、E、C三点是否在以点D为圆心,
DB长为半径的圆上,并说明理由。
A
F
D
E
C
B
综合练习
【例1】已知点A到⊙O的最近距离和最远距离分别是3cm和9cm,求⊙O的半径.
(1)当点A在⊙O内时,R=3+9=12(cm),
如图1,所以⊙O的半径是6cm.
(2)当点A在⊙O外时,R=9-3=6(cm),
如图2,所以⊙O的半径是3cm.
综上所述,⊙O的半径是6cm或3cm.
方法归纳:
点与圆有三种位置关系:
①点在圆内; ②点在圆上; ③点在圆外;
但圆上的点具有唯一性.
所以,只考虑点在圆内和点在圆外两种情况.
1.平面上有⊙O及一点P,P到⊙O上一点的距离最长为10cm,最短为4cm,则⊙O的半径为______cm.
2.点A到圆的最近距离是a,最远距离是b,则该圆的直径是
__________.
b-a或b+a
3或7
3.如图,在Rt△ABC中,∠ACB=90 ,AC=BC=2,以BC为直径的半圆交AB于点D,P是CD上的一个动点,连接AP,求AP的最小值。
⌒
P
P
A
O
B
C
D
4.如图,在矩形ABCD中,AB=4,AD=6,点E是AB边上的中点,点F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB F,连接B C,则B C最小值是_________.
A
B
E
F
C
D
B
点与圆的位置关系的多样性
由圆的对称性引起的多样性
由一弦对二弧而引起的多样性
由动点引起的直线与圆的位置多样性
知识点
【例2】已知,⊙O的直径是10cm,弦AB∥CD,AB=6cm,CD=8cm,求AB与CD之间的距离.
AB与CD之间的距离是7cm或1cm.
图1 图2
方法归纳:
①平行弦位于圆心的同侧时,平行弦之间的距离等于弦心距之差;
②平行弦位于圆心的异侧时,平行弦之间的距离等于弦心距之和.
1.在半径为5cm的⊙O中,如果弦CD=8cm,直径AB⊥CD,垂足为E,那么AE的长为__________.
2.在半径为1的⊙O中,弦AB= ,AC= ,那么∠BAC=________.
3.在直径为650mm的圆柱形油槽内装入一些油后,若油面宽
AB=600mm,求油的最大深度。
2cm或8cm
75 或15
点与圆的位置关系的多样性
由圆的对称性引起的多样性
由一弦对二弧而引起的多样性
由动点引起的直线与圆的位置多样性
知识点
【例3】弦AB的长等于半径,则AB所对的圆周角等于多少度?
解:(1)当圆周角所对的弧是劣弧时,如图:
连接OA,OB,AC,BC,得到△AOB是等边三角形
∴∠AOB=60 .∴∠ACB=0.5∠AOB=30 .
(2)当圆周角所对的弧是优弧时,如图:易得∠AC B=150 .
综上所述,弦AB所对的圆周角等于30 或150 .
方法归纳:
①一条弧对应一个圆心角和一个圆周角,
②一条弦却对一个圆心角和二个圆周角,
③同弦所对两圆周角互补.
1.⊙O为△ABC的外接圆,∠BOC=100 ,则∠A=__________.
2.已知A、B、C是⊙O上三点,且AB=AC,圆心O到BC的距离为3厘米,圆的半径为5厘米,求AB长.
50 或130
O
A
B
C
D
D
O
A
B
C
3.一弓形弦长为8cm,弓形所在的圆的半径为5cm,则弓形的高为______.
D
C
B
O
A
D
O
A
B
C
2cm或8cm
4.点O是△ABC的外心,若∠BOC=80 ,则∠BAC的度数为( )
A.40 B.100 C.40 或140 D.40 或100
C
5.已知点I是△ABC的内心,点O是△ABC的外心,若∠BOC=120 ,则∠BIC的度数为____________
6.直线AB与⊙O相切于B点,C是⊙O与OA的交点,点D是⊙O上的动点(D与B,C不重合),若∠A=40 ,则∠BDC的度数是( )
A.25 或155 B.50 或155 C.25 或130 D.50 或130
120 或150
A
点与圆的位置关系的多样性
由圆的对称性引起的多样性
由一弦对二弧而引起的多样性
由动点引起的直线与圆的位置多样性
知识点
解:过P作直线x=2的垂线,垂足为A,
当点P在直线x=2右侧时,AP=x-2=3,∴x=5.∴P(5,7.5).
当点P在x=2的左侧时,PA=2-x=3,x=-1,∴P(-1,-32).
∴当⊙P与直线x=2相切时,P点坐标为(5,7.5)或(-1,-1.5).
【例4】如图,P为正比例函数y=1.5x图象上的一个动点,⊙P的半径为3,设点P的坐标为(x,y).求⊙P与直线x=2相切时点P的坐标.
方法归纳:
由于动点的移动而导致的图形整体运动,要抓住在图形变化时几种特殊静态位置的关键要素.从而分类型以静态位置的条件达到解题的目的.
1.如图,线段OA垂直射线OB于点O,OA=4,⊙A的半径是2,将OB绕点O沿顺时针方向旋转,当OB与⊙A相切时,OB旋转的角度为__________.
60 或120
2.如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点.
(1)求证:OD⊥OC
(2)若BC=9,AD=4,求OB的长.
O
A
B
C
D
E
3.如图,已知直角梯形ABCD中,AD∥BC,∠B=90 ,AB=8cm,AD=24cm,
BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动.P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为ts,问:
(1)t为何值时,P、Q两点之间的距离为10cm
(2)t分别为何值时,直线PQ与⊙O相切 相离 相交
解:(1)AP=t,BQ=26-3t.如图1:作PE⊥BC于E,QE=26-4t.由勾股定理,得(26-4t)2+64=100,解得t=5或8.
(2)当PQ与⊙O相切时,如图2,由相切,得PQ=AP+BQ=26-2t,BE=26-4t,PE=8,(26-4t)2+64=(26-2t)2,解得t=8或2/3.即t=8或2/3时,直线PQ与⊙O相切;当26÷3=26/3,当t=26/3时运动停止,0≤t<2/3或8<t≤26/3,直线PQ与⊙O相交;2/3<t<8,直线PQ与⊙O相离.
1.如图,在☉O中,已知直径AB⊥CD于点E,∠CDB=18 .将△OBD绕点O顺时针旋转,且旋转后点B,D的对应点分别是B ,D ,使弦B D 的一个端点与弦AC的一个端点恰好重合,则弦B D 与弦AC的夹角为___________.
动态问题
54 或90
A
E
B
D
C
O
2.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心、PM的长为半径作☉P.当☉P与正方形ABCD的边相切时,BP的长为____ .
动态问题
A
B
M
P
C
D
3.如图,在平面直角坐标系中,直线y=-x+8与x轴,y轴分别交于A,B两点,☉O的半径为4,将直线AB以每秒4个单位长度的速度向下平移,设平移时间为t(s),当直线AB恰好与☉O相交时,t的整数值为___ .
1,2或3
动态问题
y
B
A
O
x
【例1】如图AB、AC是⊙O的两条弦,∠A=30 ,过点C的切线与OB的延长线交于点D,则∠D的度数为 度.
解:连接OC,
∴∠OCD=90 ,
∴∠COB=2∠A=60 ,
∴∠D=90 -∠COB=30 .
O
A
B
C
D
30
利用同弧或等弧转化圆周角与圆心角
构造圆内接四边形转化角
利用直径构造直角三角形转化角
利用特殊数量关系构造特殊角转化角
知识点
【例2】如图,已知圆心角∠AOB=110 ,则圆周角∠ACB=____度.
125
O
A
B
C
D
利用同弧或等弧转化圆周角与圆心角
构造圆内接四边形转化角
利用直径构造直角三角形转化角
利用特殊数量关系构造特殊角转化角
知识点
【例3】如图,⊙O的直径是AC,∠B=35 ,则∠DAC的度数是( )
A.60 B.55 C.50 D.40
B
O
A
C
B
D
利用同弧或等弧转化圆周角与圆心角
构造圆内接四边形转化角
利用直径构造直角三角形转化角
利用特殊数量关系构造特殊角转化角
知识点
【例4】如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,
∠P=40 ,则∠BAC的度数是( )
A.10 B.20 C.30 D.40
B
O
P
C
B
A
第24章 圆
章末复习课
与圆有关的性质
01
与圆有关的位置
02
与圆有关的计算
03
知识点
1.如图.M是CD的中点.EM⊥CD.若CD=8.EM=8.则弧CED所在圆的半径为_____.
2.在⊙O中,圆心O到弦AB的距离为AB长度的一半,则弦AB所对圆心角的大小为( )
A.30 B.45 C.60 D.90
圆的有关性质
D
E
M
D
C
5
3.如图1,四边形ABCD为⊙O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是 .
4.如图2,线段AB是直径,点D是⊙O上一点,∠CDB=20 ,过点C作⊙O的切线交AB的延长线于点E,则∠E等于 .
(
135
C
D
B
A
P
O
图1
O
C
A
B
E
D
图2
50
圆的有关性质
基础练习
5.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:△CDE是等边三角形;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
圆的有关性质
A
B
C
D
P
O
图b
1.如图b,AB是⊙O的直径,且AB=2,C,D是同一半圆上的两点,并且AC与BD的度数分别是96 和36 ,动点P是AB上的任意一点,则PC+PD的最小值是 .
(
(
2.如图,点C是扇形OAB上的AB的任意一点,OA=2,连接AC,BC,过点O作OE⊥AC,OF⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
(
A
O
B
C
E
F
圆的有关性质
圆的有关性质
3.在⊙O中,弦AB所对的圆心角∠AOB=100 则弦AB所对的圆周角为__________.
4.如图,AB是⊙O的直径,弦BC=2,F是弦BC的中点,∠ABC=60 .若动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t(s)((0<t<3)连接EF,
当t= s时,△BEF是直角三角形.
50 或130
A
B
C
E
O
F
与圆有关的性质
01
与圆有关的位置
02
与圆有关的计算
03
知识点
1.☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )
A.点A在☉O内部 B.点A在☉O上
C.点A在☉O外部 D.点A不在☉O上
2.点O是△ABC的外心,若∠BOC=80 ,则∠BAC的度数为( )
A.40 B.100 C.40 或140 D.40 或100
3.点O是△ABC的内心,若∠BAC=70 ,则∠BOC=_____.
4.在△ABC,∠C=90 ,AC=6,BC=8,则△ABC的外接圆面积是_____.
与圆有关的位置关系
D
C
125
25π
与圆有关的位置关系
1.如图,直线AB,CD相交于点O,∠AOD=30 ,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么 秒钟后⊙P与直线CD相切.
A
B
D
C
P
P1
P2
E
4或8
思路点拨:根本题应分为两种情况:(1)⊙P在直线AB下面与直线CD相切;
(2)⊙P在直线AB上面与直线CD相切.
与圆有关的位置关系
2.已知:如图,PA,PB是⊙O的切线,A、B为切点,过 上的一点C作⊙O的切线,交PA于D,交PB于E.
(1)若∠P=70 ,求∠DOE的度数;
(2)若PA=4cm,求△PDE的周长.
P
C
D
E
B
A
(1)∠DOE=55°
(2)△PDE的周长=PD+PE+DE
=PD+AD+BE+PE=2PA=8(cm)
与圆有关的性质
01
与圆有关的位置
02
与圆有关的计算
03
知识点
1.如图的扇形是一个圆锥的侧面展开图,若∠AOB=120 ,AB的长为12πcm,则该圆锥的侧面积为_____cm2.
2.如图,点A,B,C在⊙O上,⊙O的半径为9,
AB的长为2π,则∠ACB的大小是_____.
3.用一个圆心角为120 ,半径为6的扇形
作一个圆锥的侧面,这个圆锥的底面圆
的半径是____.
考点4:与圆有关的计算
108π
20
2
︵
︵
考点4:与圆有关的计算
4.(1)一条弧所对的圆心角为135 ,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 .
(2)若一个正六边形的周长为24,则该正六边形的面积为_____.
5.如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120 ,则图中阴影部分的面积等于____.
40cm
12.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是____(结果保留π)
基础练习
考点4:与圆有关的计算
5.如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上,OA=1,∠AOC=120 ,∠1=∠2,则扇形OEF的面积
基础练习
6.将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,
则这个圆锥的高为( )
A
A
B
基础练习
8.如图,已知正六边形ABCDEF内接于半径为4的⊙O,则阴影部分的面积为________.
基础练习
10.如图,将弧长为6π,圆心角为120 的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘连部分忽略不计),则圆锥形纸帽的高是____.
11.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长为____.
4π
基础练习
19.如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60 ,过点D作⊙O的切线CD交AB的延长线于点C,E为弧AD的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
考点4:与圆有关的计算
1.如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
C
A
E
F
D
C
B
考点4:与圆有关的计算
2.如下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形是扇形OAB,经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm,求
(1)扇形OAB的圆心角;
(2)这个纸杯的表面积.
(面积计算结果保留用π).
A
B
C
D
O
E
F
6cm
4cm
8cm
S纸杯表=44π(cm2).
补 充 练 习
OPTION
1.如图,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度)=那么y与点P运动的时间x(单位:秒)的关系图是( )
B
拓展提高
2.如图,根据天气预报,某台风中心位于A市正东方向300km的点O处,正以20km/h的速度向北偏西60 方向移动,距离台风中心250
km范围内都会受到影响,若台风移动的速度和方向不变,则A市受台风影响持续的时间是( )
A.10h B.20h C.30h D. 40h
B
拓展提高
北
东
A
O
M
60°
(
3.一电工沿着如图所示的梯子NL往上爬,当他爬到中点M处时,由于地面太滑,梯子沿墙面与地面滑下,设点M的坐标为(x,y)(x>0),则y与x之间的函数关系用图象表示大致是( )
C
拓展提高
L
M
N
L
M
N
y
O
x
A
y
O
x
B
y
O
x
C
y
O
x
D
4.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则EF:GH的值是( )
C
拓展提高
5.如图,点P是圆上一动点,弦AB= cm,PC平分∠APB,∠BAC=30 .当∠PAC=_ 时,四边形PACB有最大面积,此时最大面积是_ cm2
P
B
A
C
90
拓展提高
1.在⊙O中,直径AB=6,BC是弦,∠ABC=30 ,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
综合练习
A
Q
P
C
B
O
图1
A
Q
P
C
B
O
图2
综合练习
1.如图,在Rt△AOB中,OB= ,∠A=30 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),求线段PQ长度的最小值。
A
P
Q
O
B
2.如图,△ABC是⊙O的内接正三角形,P为弧BC上的一动点。
(1)求证:PA平分∠BPC.
(2)求证:PA=PB+PC.
A
P
O
C
B
D
综合练习
综合练习
3.已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接DE.
(1)若AD=DB,OC=5,求切线AC的长;
(2)求证:ED是⊙O的切线.
10
B
D
E
O
C
A
4.如图,⊙O的直径AB=4,∠ABC=30 ,BC交⊙O于D,D是BC的中点.
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,
求证:直线DE是⊙O的切线.
A
E
D
C
O
B
综合练习
5.已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D,∠DAC=20
(1)如图1,当直线l与⊙O相切于点C时,求∠BAC的大小,
(2)如图2,当直线l与⊙O相交于点C,E时,求∠BAE的大小.
O
l
C
A
D
B
如图1
O
l
C
A
D
B
E
如图2
(1)∠BAC=∠DAC=20
(2)∠BAE=∠DAC=20
综合练习
6.大练P568.如图,AD为△ABC外接圆的直径,AD⊥BC于点F,∠ABC的平分线交AD于点E,连接BD、CD.
(1)求证:BD=CD
(2)试判断B、E、C三点是否在以点D为圆心,
DB长为半径的圆上,并说明理由。
A
F
D
E
C
B
综合练习
【例1】已知点A到⊙O的最近距离和最远距离分别是3cm和9cm,求⊙O的半径.
(1)当点A在⊙O内时,R=3+9=12(cm),
如图1,所以⊙O的半径是6cm.
(2)当点A在⊙O外时,R=9-3=6(cm),
如图2,所以⊙O的半径是3cm.
综上所述,⊙O的半径是6cm或3cm.
方法归纳:
点与圆有三种位置关系:
①点在圆内; ②点在圆上; ③点在圆外;
但圆上的点具有唯一性.
所以,只考虑点在圆内和点在圆外两种情况.
1.平面上有⊙O及一点P,P到⊙O上一点的距离最长为10cm,最短为4cm,则⊙O的半径为______cm.
2.点A到圆的最近距离是a,最远距离是b,则该圆的直径是
__________.
b-a或b+a
3或7
3.如图,在Rt△ABC中,∠ACB=90 ,AC=BC=2,以BC为直径的半圆交AB于点D,P是CD上的一个动点,连接AP,求AP的最小值。
⌒
P
P
A
O
B
C
D
4.如图,在矩形ABCD中,AB=4,AD=6,点E是AB边上的中点,点F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB F,连接B C,则B C最小值是_________.
A
B
E
F
C
D
B
点与圆的位置关系的多样性
由圆的对称性引起的多样性
由一弦对二弧而引起的多样性
由动点引起的直线与圆的位置多样性
知识点
【例2】已知,⊙O的直径是10cm,弦AB∥CD,AB=6cm,CD=8cm,求AB与CD之间的距离.
AB与CD之间的距离是7cm或1cm.
图1 图2
方法归纳:
①平行弦位于圆心的同侧时,平行弦之间的距离等于弦心距之差;
②平行弦位于圆心的异侧时,平行弦之间的距离等于弦心距之和.
1.在半径为5cm的⊙O中,如果弦CD=8cm,直径AB⊥CD,垂足为E,那么AE的长为__________.
2.在半径为1的⊙O中,弦AB= ,AC= ,那么∠BAC=________.
3.在直径为650mm的圆柱形油槽内装入一些油后,若油面宽
AB=600mm,求油的最大深度。
2cm或8cm
75 或15
点与圆的位置关系的多样性
由圆的对称性引起的多样性
由一弦对二弧而引起的多样性
由动点引起的直线与圆的位置多样性
知识点
【例3】弦AB的长等于半径,则AB所对的圆周角等于多少度?
解:(1)当圆周角所对的弧是劣弧时,如图:
连接OA,OB,AC,BC,得到△AOB是等边三角形
∴∠AOB=60 .∴∠ACB=0.5∠AOB=30 .
(2)当圆周角所对的弧是优弧时,如图:易得∠AC B=150 .
综上所述,弦AB所对的圆周角等于30 或150 .
方法归纳:
①一条弧对应一个圆心角和一个圆周角,
②一条弦却对一个圆心角和二个圆周角,
③同弦所对两圆周角互补.
1.⊙O为△ABC的外接圆,∠BOC=100 ,则∠A=__________.
2.已知A、B、C是⊙O上三点,且AB=AC,圆心O到BC的距离为3厘米,圆的半径为5厘米,求AB长.
50 或130
O
A
B
C
D
D
O
A
B
C
3.一弓形弦长为8cm,弓形所在的圆的半径为5cm,则弓形的高为______.
D
C
B
O
A
D
O
A
B
C
2cm或8cm
4.点O是△ABC的外心,若∠BOC=80 ,则∠BAC的度数为( )
A.40 B.100 C.40 或140 D.40 或100
C
5.已知点I是△ABC的内心,点O是△ABC的外心,若∠BOC=120 ,则∠BIC的度数为____________
6.直线AB与⊙O相切于B点,C是⊙O与OA的交点,点D是⊙O上的动点(D与B,C不重合),若∠A=40 ,则∠BDC的度数是( )
A.25 或155 B.50 或155 C.25 或130 D.50 或130
120 或150
A
点与圆的位置关系的多样性
由圆的对称性引起的多样性
由一弦对二弧而引起的多样性
由动点引起的直线与圆的位置多样性
知识点
解:过P作直线x=2的垂线,垂足为A,
当点P在直线x=2右侧时,AP=x-2=3,∴x=5.∴P(5,7.5).
当点P在x=2的左侧时,PA=2-x=3,x=-1,∴P(-1,-32).
∴当⊙P与直线x=2相切时,P点坐标为(5,7.5)或(-1,-1.5).
【例4】如图,P为正比例函数y=1.5x图象上的一个动点,⊙P的半径为3,设点P的坐标为(x,y).求⊙P与直线x=2相切时点P的坐标.
方法归纳:
由于动点的移动而导致的图形整体运动,要抓住在图形变化时几种特殊静态位置的关键要素.从而分类型以静态位置的条件达到解题的目的.
1.如图,线段OA垂直射线OB于点O,OA=4,⊙A的半径是2,将OB绕点O沿顺时针方向旋转,当OB与⊙A相切时,OB旋转的角度为__________.
60 或120
2.如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点.
(1)求证:OD⊥OC
(2)若BC=9,AD=4,求OB的长.
O
A
B
C
D
E
3.如图,已知直角梯形ABCD中,AD∥BC,∠B=90 ,AB=8cm,AD=24cm,
BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动.P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为ts,问:
(1)t为何值时,P、Q两点之间的距离为10cm
(2)t分别为何值时,直线PQ与⊙O相切 相离 相交
解:(1)AP=t,BQ=26-3t.如图1:作PE⊥BC于E,QE=26-4t.由勾股定理,得(26-4t)2+64=100,解得t=5或8.
(2)当PQ与⊙O相切时,如图2,由相切,得PQ=AP+BQ=26-2t,BE=26-4t,PE=8,(26-4t)2+64=(26-2t)2,解得t=8或2/3.即t=8或2/3时,直线PQ与⊙O相切;当26÷3=26/3,当t=26/3时运动停止,0≤t<2/3或8<t≤26/3,直线PQ与⊙O相交;2/3<t<8,直线PQ与⊙O相离.
1.如图,在☉O中,已知直径AB⊥CD于点E,∠CDB=18 .将△OBD绕点O顺时针旋转,且旋转后点B,D的对应点分别是B ,D ,使弦B D 的一个端点与弦AC的一个端点恰好重合,则弦B D 与弦AC的夹角为___________.
动态问题
54 或90
A
E
B
D
C
O
2.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心、PM的长为半径作☉P.当☉P与正方形ABCD的边相切时,BP的长为____ .
动态问题
A
B
M
P
C
D
3.如图,在平面直角坐标系中,直线y=-x+8与x轴,y轴分别交于A,B两点,☉O的半径为4,将直线AB以每秒4个单位长度的速度向下平移,设平移时间为t(s),当直线AB恰好与☉O相交时,t的整数值为___ .
1,2或3
动态问题
y
B
A
O
x
【例1】如图AB、AC是⊙O的两条弦,∠A=30 ,过点C的切线与OB的延长线交于点D,则∠D的度数为 度.
解:连接OC,
∴∠OCD=90 ,
∴∠COB=2∠A=60 ,
∴∠D=90 -∠COB=30 .
O
A
B
C
D
30
利用同弧或等弧转化圆周角与圆心角
构造圆内接四边形转化角
利用直径构造直角三角形转化角
利用特殊数量关系构造特殊角转化角
知识点
【例2】如图,已知圆心角∠AOB=110 ,则圆周角∠ACB=____度.
125
O
A
B
C
D
利用同弧或等弧转化圆周角与圆心角
构造圆内接四边形转化角
利用直径构造直角三角形转化角
利用特殊数量关系构造特殊角转化角
知识点
【例3】如图,⊙O的直径是AC,∠B=35 ,则∠DAC的度数是( )
A.60 B.55 C.50 D.40
B
O
A
C
B
D
利用同弧或等弧转化圆周角与圆心角
构造圆内接四边形转化角
利用直径构造直角三角形转化角
利用特殊数量关系构造特殊角转化角
知识点
【例4】如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,
∠P=40 ,则∠BAC的度数是( )
A.10 B.20 C.30 D.40
B
O
P
C
B
A
同课章节目录
