5.7 三角函数的应用(1)(23页ppt)
文档属性
| 名称 | 5.7 三角函数的应用(1)(23页ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-31 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第5章 三角函数
5.7 三角函数的应用(1)
人教A版(2019)
教学目标
学习目标 数学素养
1.会用三角函数解决简单的实际问题; 1.数学抽象素养.
2.体会利用三角函数构建刻画事物周期性变化的数学模型. 2.逻辑推理素养.
3.通过三角函数模型的实际应用,使学生学会把实际问题抽象为数学问题,即建立数学模型的思想. 3.数学抽象素养.
温故知新
函数的性质
名 称 性 质
定义域
值域
周期性
对称中心
对称轴
奇偶性
单调性
R
[-A,A]
.
由.
由.
当时,是奇函数;当时是偶函数;其它情况是非奇非偶函数.
由,解得单调递增区间;
由,解得单调递减区间.
新知探究
现实生活中存在大量具有周而复始、循环往复 特点的周期运动变化现象.三角函数是基本初等函数之一,是反映周期变化现象的重要函数模型,在数学和其他领域具有重要作用,物理中的匀速圆周运动、简谐运动、交变电流问题,日常生活中的海洋潮汐问题、水车、摩天轮转动问题等都是用三角函数来模拟刻画的一些典型问题,命题时常以这些问题为背景,考查学生收集数据、拟合数据及应用已学知识处理实际问题的能力.本节课通过几个具体实例,说明三角函数模型的简单应用.
新知探究
问题1 某个弹簧振子(简称振子)在完成一次全振
动的过程中,时间t (单位s)与位移y (单位:mm)之
间的对应数据如表所示.试根据这些数据确定这个
振子的位移关于时间的函数解析式.
振子的振动具有循环往复的特点,由振子振动的物理学原来可知,其位移随时间的变化规律可以用函数来刻画.
新知探究
根据已知数据,画出散点图.
由数据表和散点图可知,振子振动的位移最大值为20mm,则A=20.
振子振动的周期为0.6s,则T=0.6,即,解得;
再由初始状态(t=0)振子的位移为-20,可得
,即.
则.
所以振子位移关于时间的函数解析式为
.
新知探究
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的震动,等等.这些都是物体在某一中心位置附近循环往复的运动.
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.可以证明,在适当的坐标系下,简谐运动可以用函数y=Asin(ωx+φ),x∈[0,+∞)表示,其中A>0,ω>0.描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
A就是这个简谐运动的振幅,它是作简谐运动的物体离开平衡位置的最大距离;
简谐运动的周期是,它是作简谐运动的物体往复运动一次所需要的时间;
简谐运动的频率由公式,它是作简谐运动的物体在单位时间内往复运动的次数;
ωx+φ称为相位;x=0时的相位φ称为初相.
新知探究
在中各参数的物理意义.
做简谐运动的物体离开平衡位置的最大距离;
做简谐运动的物体往复运动一次所需要的时间;
做简谐运动的物体在单位时间内往复运动的次数;
周期
频率
振幅
ωx+φ 称为相位;
x=0 时的相位 φ 称为初相.
新知探究
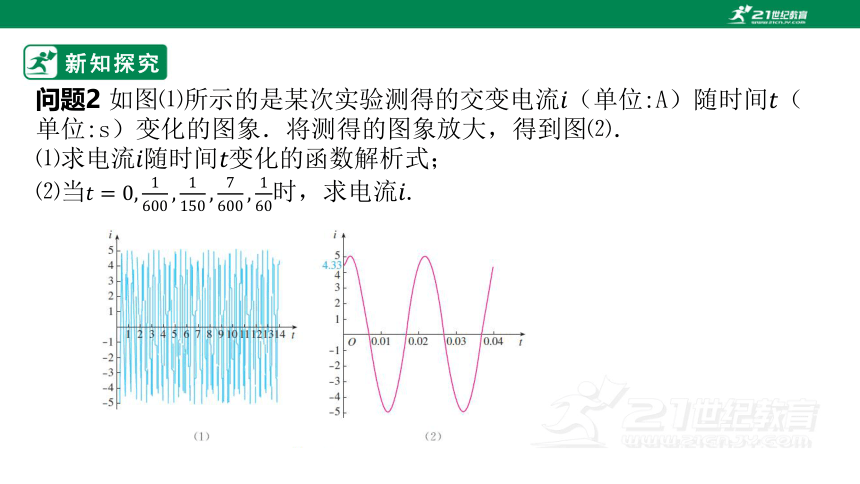
问题2 如图⑴所示的是某次实验测得的交变电流(单位:A)随时间(单位:s)变化的图象.将测得的图象放大,得到图⑵.
⑴求电流随时间变化的函数解析式;
⑵当时,求电流.
新知探究
解:
⑴由交变电流的产生原理可知,电流随时间的变化规律可用来刻画,其中表示频率,表示振幅,表示初相.
由图⑵可知,电流最大值为5A,因此;
电流变化的周期为,频率为50Hz,
即,解得;
再由初始状态()的电流约为 4.33A,
可得,因此约为.
所以电流随时间变化的函数解析式是
.
新知探究
解:
⑵由⑴知,电流随时间变化的函数解析式是
.
当时,;
当时,;
当时,;
当时,;
当时,.
新知探究
【例1】已知弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移(单位:cm)随时间(单位:s)的变化规律为.根据题意,回答下列问题:
⑴小球在开始振动()时的位移是多少?
⑵小球升高到最高点和下降到最低点的位移分别是多少?
⑶经过多长时间小球往复振动一次?振动的频率是多少?
⑷小球在s经过最高点的次数恰为50次,求的范围.
解:
⑴将代入,得.
⑵小球上升到最高点和下降到最低点的位移分别是4cm和-4cm.
所以小球在开始振动时的位移是.
⑶因为函数s的周期是,所以小球往复振动一次所用的时间是s.
振动的频率是.
新知探究
【例1】已知弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移(单位:cm)随时间(单位:s)的变化规律为.根据题意,回答下列问题:
⑴小球在开始振动()时的位移是多少?
⑵小球升高到最高点和下降到最低点的位移分别是多少?
⑶经过多长时间小球往复振动一次?振动的频率是多少?
⑷小球在s内经过最高点的次数恰为50次,求的范围.
解:
⑷由题意得,当时,小球第一次到达最高点,以后每隔一个周期都出现一次最高点.
∴,
∵小球在s内经过最高点的次数恰为50次,
又∵,即 .
∴的取值范围是.
初试身手
1.⑴简谐运动的相位与初相是 ( )
A., B.,4
C., D.4,
⑵最大值是,最小正周期是,初相为的函数解析式是( )
A. B. C. D.
解:
⑴相位是,当时为初相即.故选C.
⑵由最小正周期是,得.
∵初相为, ∴函数解析式为.故选D.
C
D
初试身手
1.某简谐运动得图象如图所示,试根据图象回答下列问题:
⑴这个简谐运动得振幅、周期和频率各是多少?
⑵写出这个简谐运动的函数解析式.
解:
⑴由图可得,即,
⑵由⑴,得.
设此函数解析式是
∴.
P244 练习
∵,
∴,解得
则此函数解析式是.
第⑵问思路2:得到,按照图象变换,看成由图象向左平移个单位长度得到,因此,函数解析式为:
.
初试身手
2.如图,一根绝对刚性且长度不变、质量可忽略不计的线,
一端固定,另一端悬挂一个沙漏.让沙漏在偏离平衡位置
一定角度(最大偏角)后在重力作用下铅锤面内做周期摆
动.若线长lcm,沙漏摆动时离开平衡位置的位移为s(单
位:cm)与时间t(单位:s)的函数关系是
⑴当时,求该沙漏的最大偏角(精确到0.0001);
⑵已知g=9.8m/s2,要使沙漏摆动的周期是1s,线的长度应当是多少(精确0.1cm)
解:
⑴∵, ∴的最大值为3.
则当时,该沙漏的最大偏角是0.1203rad.
P244 练习
设偏角为,可得最大偏角满足.利用计算器计算可得θ=0.1203rad.
初试身手
2.如图,一根绝对刚性且长度不变、质量可忽略不计的线,
一端固定,另一端悬挂一个沙漏.让沙漏在偏离平衡位置
一定角度(最大偏角)后在重力作用下铅锤面内做周期摆
动.若线长lcm,沙漏摆动时离开平衡位置的位移为s(单
位:cm)与时间t(单位:s)的函数关系是
⑴当时,求该沙漏的最大偏角(精确到0.0001);
⑵已知g=9.8m/s2,要使沙漏摆动的周期是1 s,线的长度应当是多少(精确0.1cm)
解:
⑴∵沙漏摆动的周期,
则要使沙漏摆动的周期是1 s,线的长度应当是24.8cm.
P244 练习
∴(cm).
初试身手
3.一台发电机产生的电流是正弦式电流,电压和时间之间的关系如图所示.由图象说出它的周期、频率和电压的最大值,并求出电压(单位:V)关于时间(单位:s)的函数解析式.
解:
设电压关于时间的函数是.
根据图象可得,振幅,周期s.
∴频率.电压的最大值(v).
∴.
则电压关于时间的函数是.
又∵图象过原点,∴.
课堂小结
1.用函数y=Asin(ωx+φ),x∈[0,+∞)表示,其中A>0,ω>0.描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
2.根据实际问题,建立函数的模型
A就是这个简谐运动的振幅,它是作简谐运动的物体离开平衡位置的最大距离;
简谐运动的周期是,它是作简谐运动的物体往复运动一次所需要的时间;
简谐运动的频率由公式,它是作简谐运动的物体在单位时间内往复运动的次数;
ωx+φ称为相位;x=0时的相位φ称为初相.
作业布置
作业:P249 习题5.7 第1,2题.
补充:
1.如图,单摆从某点开始来回摆动,离开平衡位置O的距离s cm和时间t s的函数关系式为,那么单摆来回摆动一次所需的时间为( )
A.s B.s C.0.5s D.1s
2.商场人流量被定义为每分钟通过入口的人数,劳动节某商场的人流量满足函数(t≥0),则在下列哪个时间段内人流量是增加的( )
A.[0,5] B.[5,10] C.[10,15] D.[15,20]
3.如图,是一弹簧振子做简谐振动的图象,
横轴表示振动的时间,纵轴表示振子的位移,
则这个振子振动的函数解析式为 .
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第5章 三角函数
5.7 三角函数的应用(1)
人教A版(2019)
教学目标
学习目标 数学素养
1.会用三角函数解决简单的实际问题; 1.数学抽象素养.
2.体会利用三角函数构建刻画事物周期性变化的数学模型. 2.逻辑推理素养.
3.通过三角函数模型的实际应用,使学生学会把实际问题抽象为数学问题,即建立数学模型的思想. 3.数学抽象素养.
温故知新
函数的性质
名 称 性 质
定义域
值域
周期性
对称中心
对称轴
奇偶性
单调性
R
[-A,A]
.
由.
由.
当时,是奇函数;当时是偶函数;其它情况是非奇非偶函数.
由,解得单调递增区间;
由,解得单调递减区间.
新知探究
现实生活中存在大量具有周而复始、循环往复 特点的周期运动变化现象.三角函数是基本初等函数之一,是反映周期变化现象的重要函数模型,在数学和其他领域具有重要作用,物理中的匀速圆周运动、简谐运动、交变电流问题,日常生活中的海洋潮汐问题、水车、摩天轮转动问题等都是用三角函数来模拟刻画的一些典型问题,命题时常以这些问题为背景,考查学生收集数据、拟合数据及应用已学知识处理实际问题的能力.本节课通过几个具体实例,说明三角函数模型的简单应用.
新知探究
问题1 某个弹簧振子(简称振子)在完成一次全振
动的过程中,时间t (单位s)与位移y (单位:mm)之
间的对应数据如表所示.试根据这些数据确定这个
振子的位移关于时间的函数解析式.
振子的振动具有循环往复的特点,由振子振动的物理学原来可知,其位移随时间的变化规律可以用函数来刻画.
新知探究
根据已知数据,画出散点图.
由数据表和散点图可知,振子振动的位移最大值为20mm,则A=20.
振子振动的周期为0.6s,则T=0.6,即,解得;
再由初始状态(t=0)振子的位移为-20,可得
,即.
则.
所以振子位移关于时间的函数解析式为
.
新知探究
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的震动,等等.这些都是物体在某一中心位置附近循环往复的运动.
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.可以证明,在适当的坐标系下,简谐运动可以用函数y=Asin(ωx+φ),x∈[0,+∞)表示,其中A>0,ω>0.描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
A就是这个简谐运动的振幅,它是作简谐运动的物体离开平衡位置的最大距离;
简谐运动的周期是,它是作简谐运动的物体往复运动一次所需要的时间;
简谐运动的频率由公式,它是作简谐运动的物体在单位时间内往复运动的次数;
ωx+φ称为相位;x=0时的相位φ称为初相.
新知探究
在中各参数的物理意义.
做简谐运动的物体离开平衡位置的最大距离;
做简谐运动的物体往复运动一次所需要的时间;
做简谐运动的物体在单位时间内往复运动的次数;
周期
频率
振幅
ωx+φ 称为相位;
x=0 时的相位 φ 称为初相.
新知探究
问题2 如图⑴所示的是某次实验测得的交变电流(单位:A)随时间(单位:s)变化的图象.将测得的图象放大,得到图⑵.
⑴求电流随时间变化的函数解析式;
⑵当时,求电流.
新知探究
解:
⑴由交变电流的产生原理可知,电流随时间的变化规律可用来刻画,其中表示频率,表示振幅,表示初相.
由图⑵可知,电流最大值为5A,因此;
电流变化的周期为,频率为50Hz,
即,解得;
再由初始状态()的电流约为 4.33A,
可得,因此约为.
所以电流随时间变化的函数解析式是
.
新知探究
解:
⑵由⑴知,电流随时间变化的函数解析式是
.
当时,;
当时,;
当时,;
当时,;
当时,.
新知探究
【例1】已知弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移(单位:cm)随时间(单位:s)的变化规律为.根据题意,回答下列问题:
⑴小球在开始振动()时的位移是多少?
⑵小球升高到最高点和下降到最低点的位移分别是多少?
⑶经过多长时间小球往复振动一次?振动的频率是多少?
⑷小球在s经过最高点的次数恰为50次,求的范围.
解:
⑴将代入,得.
⑵小球上升到最高点和下降到最低点的位移分别是4cm和-4cm.
所以小球在开始振动时的位移是.
⑶因为函数s的周期是,所以小球往复振动一次所用的时间是s.
振动的频率是.
新知探究
【例1】已知弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移(单位:cm)随时间(单位:s)的变化规律为.根据题意,回答下列问题:
⑴小球在开始振动()时的位移是多少?
⑵小球升高到最高点和下降到最低点的位移分别是多少?
⑶经过多长时间小球往复振动一次?振动的频率是多少?
⑷小球在s内经过最高点的次数恰为50次,求的范围.
解:
⑷由题意得,当时,小球第一次到达最高点,以后每隔一个周期都出现一次最高点.
∴,
∵小球在s内经过最高点的次数恰为50次,
又∵,即 .
∴的取值范围是.
初试身手
1.⑴简谐运动的相位与初相是 ( )
A., B.,4
C., D.4,
⑵最大值是,最小正周期是,初相为的函数解析式是( )
A. B. C. D.
解:
⑴相位是,当时为初相即.故选C.
⑵由最小正周期是,得.
∵初相为, ∴函数解析式为.故选D.
C
D
初试身手
1.某简谐运动得图象如图所示,试根据图象回答下列问题:
⑴这个简谐运动得振幅、周期和频率各是多少?
⑵写出这个简谐运动的函数解析式.
解:
⑴由图可得,即,
⑵由⑴,得.
设此函数解析式是
∴.
P244 练习
∵,
∴,解得
则此函数解析式是.
第⑵问思路2:得到,按照图象变换,看成由图象向左平移个单位长度得到,因此,函数解析式为:
.
初试身手
2.如图,一根绝对刚性且长度不变、质量可忽略不计的线,
一端固定,另一端悬挂一个沙漏.让沙漏在偏离平衡位置
一定角度(最大偏角)后在重力作用下铅锤面内做周期摆
动.若线长lcm,沙漏摆动时离开平衡位置的位移为s(单
位:cm)与时间t(单位:s)的函数关系是
⑴当时,求该沙漏的最大偏角(精确到0.0001);
⑵已知g=9.8m/s2,要使沙漏摆动的周期是1s,线的长度应当是多少(精确0.1cm)
解:
⑴∵, ∴的最大值为3.
则当时,该沙漏的最大偏角是0.1203rad.
P244 练习
设偏角为,可得最大偏角满足.利用计算器计算可得θ=0.1203rad.
初试身手
2.如图,一根绝对刚性且长度不变、质量可忽略不计的线,
一端固定,另一端悬挂一个沙漏.让沙漏在偏离平衡位置
一定角度(最大偏角)后在重力作用下铅锤面内做周期摆
动.若线长lcm,沙漏摆动时离开平衡位置的位移为s(单
位:cm)与时间t(单位:s)的函数关系是
⑴当时,求该沙漏的最大偏角(精确到0.0001);
⑵已知g=9.8m/s2,要使沙漏摆动的周期是1 s,线的长度应当是多少(精确0.1cm)
解:
⑴∵沙漏摆动的周期,
则要使沙漏摆动的周期是1 s,线的长度应当是24.8cm.
P244 练习
∴(cm).
初试身手
3.一台发电机产生的电流是正弦式电流,电压和时间之间的关系如图所示.由图象说出它的周期、频率和电压的最大值,并求出电压(单位:V)关于时间(单位:s)的函数解析式.
解:
设电压关于时间的函数是.
根据图象可得,振幅,周期s.
∴频率.电压的最大值(v).
∴.
则电压关于时间的函数是.
又∵图象过原点,∴.
课堂小结
1.用函数y=Asin(ωx+φ),x∈[0,+∞)表示,其中A>0,ω>0.描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
2.根据实际问题,建立函数的模型
A就是这个简谐运动的振幅,它是作简谐运动的物体离开平衡位置的最大距离;
简谐运动的周期是,它是作简谐运动的物体往复运动一次所需要的时间;
简谐运动的频率由公式,它是作简谐运动的物体在单位时间内往复运动的次数;
ωx+φ称为相位;x=0时的相位φ称为初相.
作业布置
作业:P249 习题5.7 第1,2题.
补充:
1.如图,单摆从某点开始来回摆动,离开平衡位置O的距离s cm和时间t s的函数关系式为,那么单摆来回摆动一次所需的时间为( )
A.s B.s C.0.5s D.1s
2.商场人流量被定义为每分钟通过入口的人数,劳动节某商场的人流量满足函数(t≥0),则在下列哪个时间段内人流量是增加的( )
A.[0,5] B.[5,10] C.[10,15] D.[15,20]
3.如图,是一弹簧振子做简谐振动的图象,
横轴表示振动的时间,纵轴表示振子的位移,
则这个振子振动的函数解析式为 .
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
